
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 10
J'apprends
Fonctions
10 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Notion et vocabulaire
Je perfectionne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Une fonction f est un processus qui, à un nombre x, fait correspondre un nombre noté f (x).
- f (x) se lit « f de x ».
- x est appelé la « variable » et f (x) est la valeur prise par la fonction f pour la valeur x.
- On note f : x \mapsto f (x) et on lit « fonction f qui à x associe f (x) ».
Exercices n° p. 220, 221
Aide
Une fonction agit comme une machine à nombre.
On rentre un nombre dans la machine afin de lui faire subir un certain nombre dʼopérations et on obtient un autre nombre.
On rentre un nombre dans la machine afin de lui faire subir un certain nombre dʼopérations et on obtient un autre nombre.
J'applique
Consigne : Quelle est la fonction qui à un nombre x associe son double ?Correction : f : x \mapsto 2x
Le nombre f(x) est alors le double de x, soit 2 \times x.
Définitions
On définit la fonction f telle que f : x \mapsto f (x), alors :
 Lʼimage dʼun nombre est unique.
Lʼimage dʼun nombre est unique.
Un nombre peut avoir un, plusieurs ou aucun antécédents par f.
- le nombre f (x) est lʼimage de x par la fonction f ;
- x est un antécédent de f (x).

Le zoom est accessible dans la version Premium.
Un nombre peut avoir un, plusieurs ou aucun antécédents par f.
Exercices n° p. 220, 221
J'applique
Consigne : f : x \mapsto x^2 + 6x
Quelles sont les images de 0, -2 et -6 par f?
Correction :
Quelles sont les images de 0, -2 et -6 par f?
Correction :
- L'image de 0 par f est : f(0) = 0^2 + 6 \times 0 = 0.
- L'image de -2 par f est : f(-2) = (-2)^2 + 6 \times (-2) donc f(-2) = -8.
- L'image de -6 par f est : f(-6) = (-6)^2 + 6 \times (-6) donc f(-6) = 0.
Consigne : f : x \mapsto x^2
Donnez des antécédents de 9, 0 et -4 par f.
Correction :
Donnez des antécédents de 9, 0 et -4 par f.
Correction :
- 9 a deux antécédents par f : 3 et -3 car f(3) = 9 et f(-3) = 9.
- 0 est l'antécédent de 0 par f car f(0) = 0.
- -4 n'a pas d'antécédent par f car il n'existe aucun nombre dont le carré soit égal à -4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Représentation dʼune fonction
Je perfectionne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Représentation graphique
Représentation
Dans un repère, la courbe représentative (ou représentation graphique) dʼune fonction f est lʼensemble des points de coordonnées (x ; f (x)).
On note généralement cette courbe représentative C_f.

On note généralement cette courbe représentative C_f.

Le zoom est accessible dans la version Premium.
Exercices n° p. 223, 224
Méthode
À lʼaide dʼune représentation graphique, on peut trouver les images et antécédents dʼune fonction.


Le zoom est accessible dans la version Premium.
Exercices n° p. 223, 224
J'applique
Consigne : a. À partir du graphique ci-dessus, lire l'image de -1.
b. À partir du graphique ci-dessus, lire les antécédents de -2.
Correction :
a. L'image de -1 est 2.
b. -2 a deux antécédents : -2 et 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Représentation dans un tableau de valeurs
Représentation
Un tableau de valeurs contient quelques valeurs prises par une fonction f.
On peut représenter les points correspondants dans un repère : ils se trouvent sur la courbe de f.
On peut représenter les points correspondants dans un repère : ils se trouvent sur la courbe de f.
Exercices n° p. 222
J'applique
Consigne : | x | -1 | 0 | 1 | 2 | 3 |
| f(x) | -5 | -3 | -1 | 1 | 1 |
Ce tableau donne quelques valeurs représentant une fonction f.
Quel est l'antécédent de -1 par f ?
Quelle est l'image de -1 par f ?
Correction :
L'antécédent de -1 par f est 1 (3e colonne).
L'image de -1 par f est -5 (1re colonne).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C Fonctions linéaires
Je perfectionne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Notion de fonction linéaire
Définition
Pour un nombre a donné, la fonction qui, à x, associe ax, est une fonction linéaire.
On la note f : x \mapsto ax
On la note f : x \mapsto ax
Exercices n° p. 224, 225
Remarque :
Les fonctions linéaires sont les fonctions f pour lesquelles f (x) est proportionnel à x. Si f : x \mapsto ax , alors a est le coefficient de proportionnalité entre x et f (x).
Un tableau de valeurs associé à une fonction linéaire est un tableau de proportionnalité.
Un tableau de valeurs associé à une fonction linéaire est un tableau de proportionnalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Représentation graphique
Représentation
La courbe de la fonction linéaire f : x \mapsto ax est une droite passant par lʼorigine du repère.
Le nombre a sʼappelle le coefficient directeur, ou « pente », de cette droite.
Le nombre a sʼappelle le coefficient directeur, ou « pente », de cette droite.
Exercices n° p. 224, 225
Aide
Toute droite non verticale passant par lʼorigine du repère est la courbe dʼune fonction linéaire.
J'applique
Consigne : Tracez la courbe représentative de la fonction linéaire f : x \mapsto 2x.

Le zoom est accessible dans la version Premium.
Correction : Cʼest une droite donc deux points suffisent pour tracer sa représentation graphique.
- Une fonction linéaire passe toujours par lʼorigine du repère, donc un des points peut être O (0 ; 0).
- f(2) = 4 donc la droite va passer par le point A (2 ; 4).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
D Fonctions affines
Je perfectionne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Notion de fonction affine
Définition
Pour deux nombres a et b donnés, la fonction qui, à x, associe ax + b est une fonction affine.
On la note f : x \mapsto ax + b.
On la note f : x \mapsto ax + b.
Exercices n° p. 224, 225
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Représentation graphique
Représentation
La courbe dʼune fonction affine f : x \mapsto ax + b est une droite.
Le nombre a sʼappelle le « coefficient directeur », ou pente, de la droite.
Le nombre b sʼappelle « lʼordonnée à lʼorigine » de la droite.

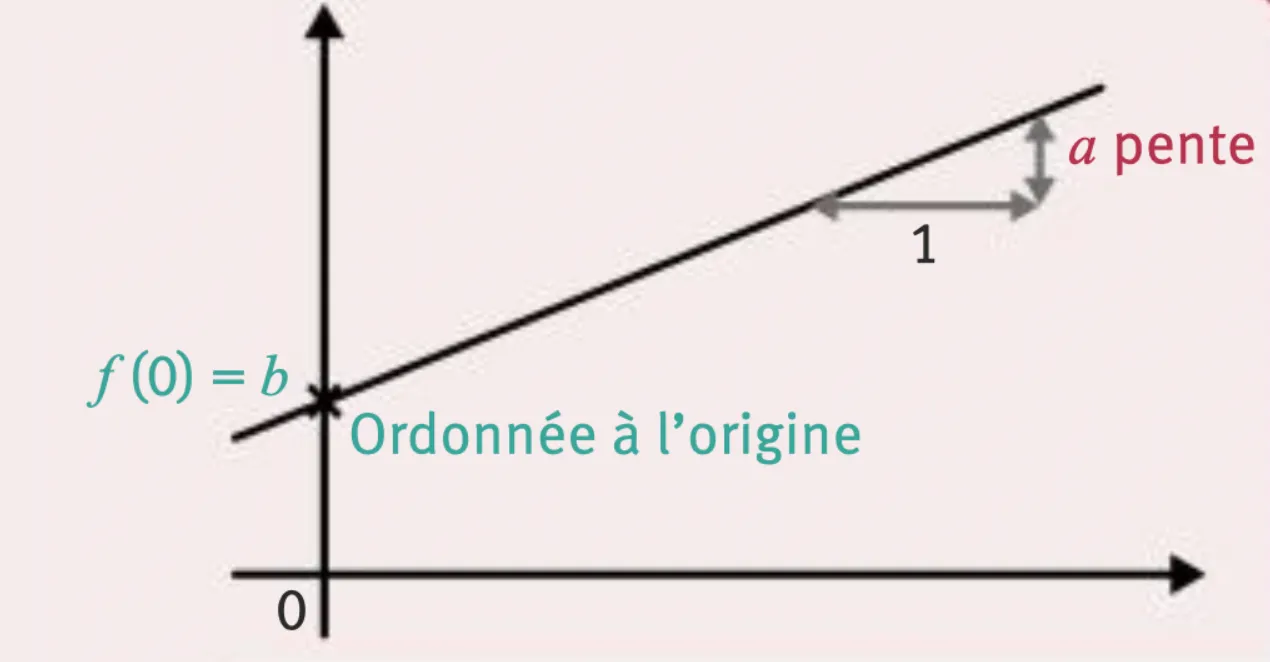
Le nombre a sʼappelle le « coefficient directeur », ou pente, de la droite.
Le nombre b sʼappelle « lʼordonnée à lʼorigine » de la droite.


Le zoom est accessible dans la version Premium.
Exercices n° p. 224, 225
- Une droite non verticale est toujours la courbe dʼune fonction affine.
- Pour un nombre b, la fonction f : x \mapsto b est affine (cʼest bien une fonction de type x \mapsto ax + b avec a = 0). Elle ne prend quʼune valeur : b. On dit que cette fonction est constante. Sa courbe est une droite horizontale.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Résolution graphique dʼune équation, dʼune inéquation
Méthode
Si a \neq c, les courbes des fonctions f : x \mapsto ax + b et g : x \mapsto cx + d sont des droites non parallèles.
Elles ont un point dʼintersection dont lʼabscisse est la solution de lʼéquation f (x) = g (x).
On peut aussi visualiser les solutions des équations f (x)~\text{\textless}~g(x), f (x) > g (x).
Elles ont un point dʼintersection dont lʼabscisse est la solution de lʼéquation f (x) = g (x).
On peut aussi visualiser les solutions des équations f (x)~\text{\textless}~g(x), f (x) > g (x).
Exercices n° p. 224, 225

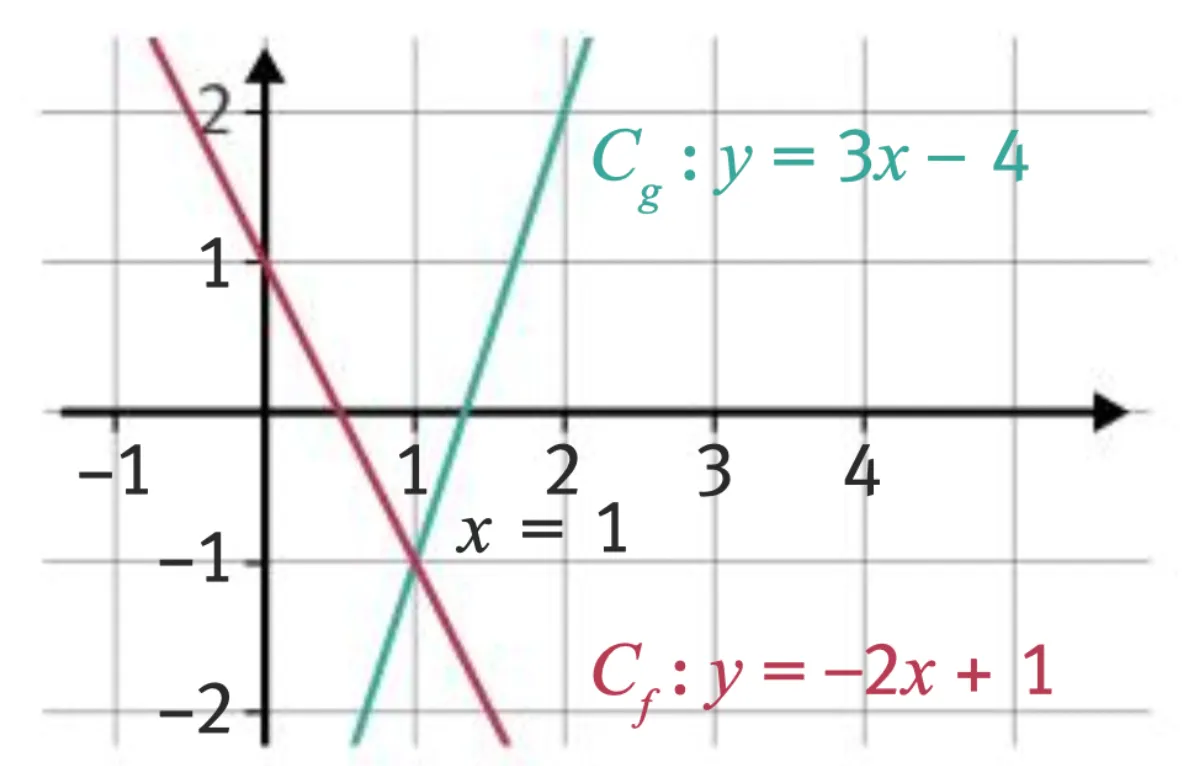
Le zoom est accessible dans la version Premium.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais

 Yolène
Yolène Émilie
Émilie Jean-Paul
Jean-Paul Fatima
Fatima Sarah
Sarah