Chapitre 4
Problèmes à résoudre
Évolution temporelle d'une transformation chimique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35Équation différentielle et concentration
✔ REA/MATH : Résoudre une équation différentielle
✔ APP : Extraire l'information utile
Établir la relation entre le temps de demi-réaction t_{1/2} et k la constante de vitesse, correspondant au coefficient de proportionnalité entre la vitesse volumique de disparition d'un réactif \text{X}(\text{aq}) et sa concentration, dont la cinétique suit une loi d'ordre 1.
Doc.1
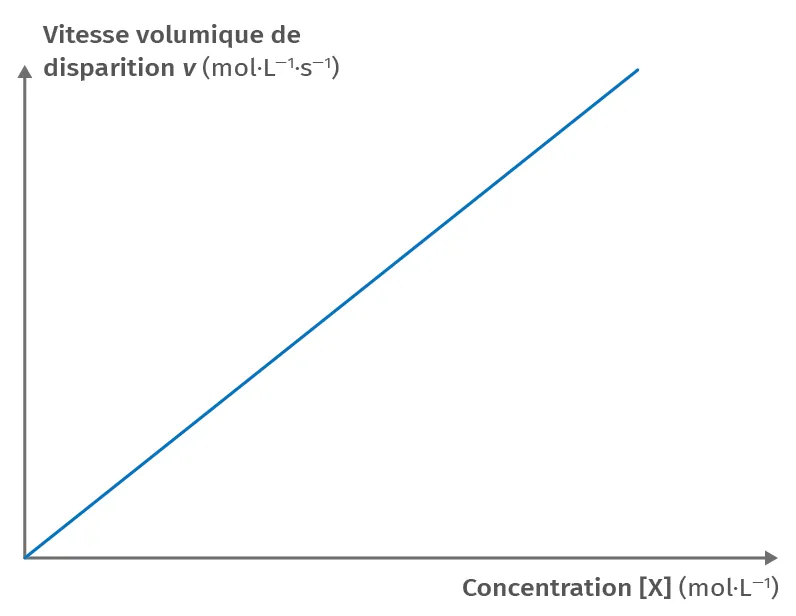
Courbe représentation de v = f([\text{X}])
Pour une réaction dont la cinétique suit une loi d'ordre 1 par rapport à la disparition du réactif \text{X}(\text{aq}), la vitesse volumique v de disparition de \text{X}(\text{aq}) s'écrit :
v = k \cdot [\text{X}]



Doc.2
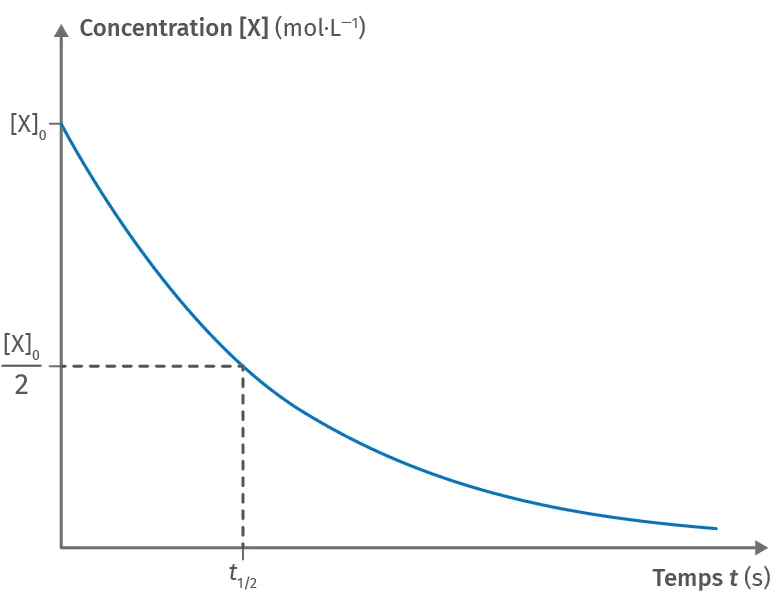
Courbe représentative de [\text{X}] = f(t)
À t = t_{1/2}, la concentration de l'espèce chimique \text{X}(\text{aq}) a diminué de moitié pour une réaction totale. On peut alors considérer que :
[\text{X}](t_{1/2}) = \dfrac{[\text{X}]_0}{2}



Doc.3
Résolution d'une équation différentielle
Une équation différentielle linéaire homogène d'ordre 1 est une équation de la forme :
Si a et b sont des coefficients constants, la solution de cette équation différentielle est de la forme :
La constante C d'intégration peut être déterminée à partir des conditions initiales pour x(t = 0 \ \text{s}) = x_0
a \cdot \dfrac{\text{d}x}{\text{d}t} + b \cdot x(t) = 0
Si a et b sont des coefficients constants, la solution de cette équation différentielle est de la forme :
x(t) = C \cdot \exp \bigg(-\dfrac{b}{a} \cdot t \bigg)
La constante C d'intégration peut être déterminée à partir des conditions initiales pour x(t = 0 \ \text{s}) = x_0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retour sur la problématique du chapitre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36Rouille
✔ RAI/MOD : Modéliser une transformation
✔ APP : Formuler des hypothèses
Lorsque du fer solide \text{Fe}(\text{s}) est en contact avec de l'eau \text{H}_2\text{O}(\text{l}) et du dioxygène \text{O}_2(\text{aq}), il s'oxyde lentement en hydroxyde de fer \text{Fe}(\text{OH})_2(\text{s}). Cet hydroxyde réagit instantanément avec l'eau \text{H}_2\text{O}(\text{l}) et le dioxygène \text{O}_2(\text{aq}) pour former un second hydroxyde selon l'équation de réaction :
Enfin, cette dernière espèce chimique se transforme spontanément en oxyde de fer par déshydratation :
✔ APP : Formuler des hypothèses
Lorsque du fer solide \text{Fe}(\text{s}) est en contact avec de l'eau \text{H}_2\text{O}(\text{l}) et du dioxygène \text{O}_2(\text{aq}), il s'oxyde lentement en hydroxyde de fer \text{Fe}(\text{OH})_2(\text{s}). Cet hydroxyde réagit instantanément avec l'eau \text{H}_2\text{O}(\text{l}) et le dioxygène \text{O}_2(\text{aq}) pour former un second hydroxyde selon l'équation de réaction :
4\ \text{Fe}(\text{OH})_2(\text{s}) \ + \ 2\ \text{H}_2\text{O}(\text{l})\ +\ \text{O}_2(\text{aq}) \rightarrow \ 4\ \text{Fe}(\text{OH})_3(\text{s})
Enfin, cette dernière espèce chimique se transforme spontanément en oxyde de fer par déshydratation :
2\ \text{Fe}(\text{OH})_3(\text{s}) \rightarrow \ \text{Fe}_2\text{O}_3(\text{s})\ +\ 3\ \text{H}_2\text{O}(\text{l})


1.
Écrire l'équation de la première réaction
évoquée dans l'énoncé.
Cette transformation est plus rapide dans une eau acidifiée, riche en ion \text{H}^+(\text{aq}).
2. Qualifier les ions \text{H}^+(\text{aq}) pour leur rôle dans la cinétique de la réaction.
Cette transformation est plus rapide dans une eau acidifiée, riche en ion \text{H}^+(\text{aq}).
2. Qualifier les ions \text{H}^+(\text{aq}) pour leur rôle dans la cinétique de la réaction.
Fermer
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
