Chapitre 13
Fiche de révision
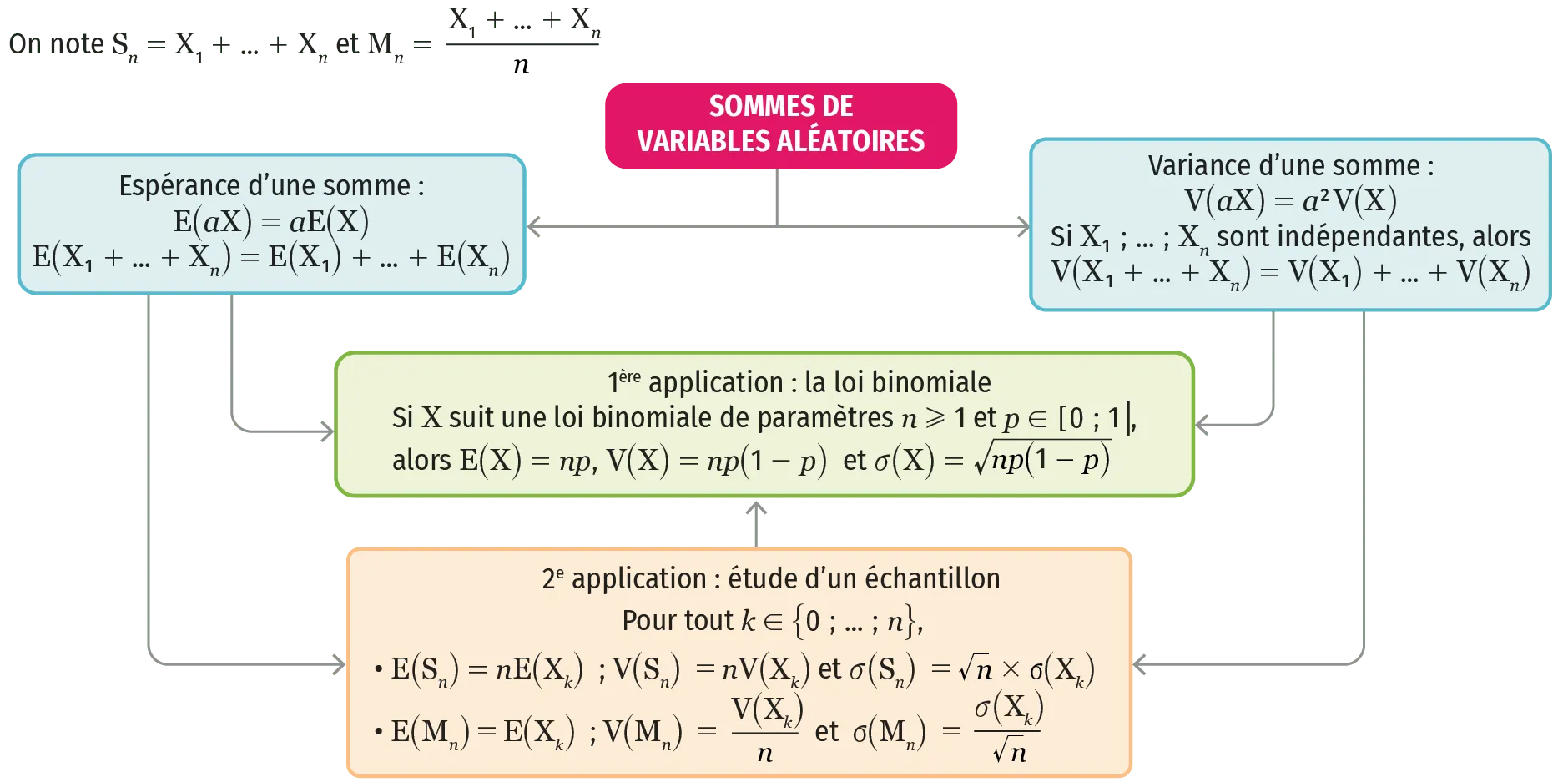
Sommes de variables aléatoires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'essentiel
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Si \textbf{X} et \textbf{Y} sont deux variables aléatoires définies sur un univers \Omega et si \boldsymbol{a} est un nombre réel, on a les égalités \mathbf{E}(\mathbf{X}+\mathbf{Y})=\mathbf{E}(\mathbf{X})+\mathbf{E}(\mathbf{Y}), \mathbf{E}(\boldsymbol{a} \mathbf{X})=\boldsymbol{a} \mathbf{E}(\mathbf{X}) \operatorname{et} \mathbf{E}(\boldsymbol{a} \mathbf{X}+\mathbf{Y})=\boldsymbol{a} \mathbf{E}(\mathbf{X})+\mathbf{E}(\mathbf{Y}). Cela permet de :
✔ déterminer l'espérance d'une variable aléatoire en la décomposant comme somme de variables aléatoires plus simples à étudier ;
✔ démontrer que si \text{X} suit la loi binomiale de paramètres n et p, alors \mathrm{E}(\mathrm{X})=n p.
2 Si \textbf{X} et \textbf{Y} sont deux variables aléatoires indépendantes définies sur un univers \Omega et si \boldsymbol{a} est un nombre réel, on a les égalités \mathbf{V}(\mathbf{X}+\mathbf{Y})=\mathbf{V}(\mathbf{X})+\mathbf{V}(\mathbf{Y}) \text { et } \mathbf{V}(\boldsymbol{a} \mathbf{X})=\boldsymbol{a}^{2} \mathbf{V}(\mathbf{X}). :
✔ déterminer la variance d'une variable aléatoire en la décomposant comme somme de variables aléatoires indépendantes plus simples à étudier ;
✔ démontrer que si \text{X} suit la loi binomiale de paramètres n et p, alors \mathrm{V}(\mathrm{X})=n p(1-p) et \sigma(\mathrm{X})=\sqrt{n p(1-p)}.
3 Étude de la somme \mathbf{S}_{n} de n variables aléatoires indépendantes \mathbf{X}_{1} ; \ldots ; \mathbf{X}_{n} suivant la même loi de
probabilité. La variable aléatoire \mathbf{S}_{n} s'écrit \mathbf{S}_{n}=\mathbf{X}_{1}+\ldots+\mathbf{X}_{n}. Cela permet de :
✔ étudier plus simplement les propriétés de la somme, notamment dans le cas de la répétition de
n expériences dans des conditions indépendantes ;
✔ calculer l'espérance de \mathrm{S}_{n} en utilisant, pour tout k \in\{1 \: ; \ldots \: ; n\}, \mathrm{E}\left(\mathrm{S}_{n}\right)=n \mathrm{E}\left(\mathrm{X}_{k}\right) ;
✔ calculer l'espérance de \mathrm{S}_{n} en utilisant \mathrm{V}\left(\mathrm{S}_{n}\right)=n \mathrm{V}\left(\mathrm{X}_{k}\right). On a ainsi \sigma\left(\mathrm{S}_{n}\right)=\sqrt{n} \sigma\left(\mathrm{X}_{k}\right).
4 Étude de la moyenne \mathbf{M}_{n} de n variables aléatoires indépendantes \mathbf{X}_{1} ; \ldots ; \mathbf{X}_{n} suivant la même loi de probabilité. La variable aléatoire \mathbf{M}_{n} s'écrit \mathbf{M}_{n}=\frac{\mathbf{X}_{1}+\ldots+\mathbf{X}_{n}}{\mathbf{n}}. Cela permet de :
✔ étudier plus simplement les propriétés de la moyenne, notamment dans le cas de la répétition de
n expériences dans des conditions indépendantes ;
✔ calculer l'espérance de \mathbf{M}_{n} en utilisant, pour tout k \in\{1 \: ; \ldots \: ; n\}, \mathrm{E}\left(\mathrm{M}_{n}\right)=\mathrm{E}\left(\mathrm{X}_{k}\right) ;
✔ calculer l'espérance de \mathbf{M}_{n} en utilisant V\left(M_{n}\right)=\frac{V\left(X_{k}\right)}{n}. On a ainsi \sigma\left(\mathrm{M}_{n}\right)=\frac{\sigma\left(\mathrm{X}_{k}\right)}{\sqrt{n}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Carte mentale

Fermer
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
