Chapitre 11
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je me teste
Je sais
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1L'unité de vitesse du système international est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2La vitesse du son dans l'air est d'environ :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3La vitesse de la lumière dans le vide est d'environ :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Pour exprimer les grandes distances de l'univers, on utilise :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5 Ordres de grandeur de quelques vitesses.
Associe à chacun de ces mobiles ou signaux sa vitesse de déplacement dans l'air.
| Lumière | |
| Son | |
| Voiture | |
| TGV | |
| Usain Bolt |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Complète la grille de mots-croisés. Pour écrire sur ce schéma, veuillez cliquer sur l'image et utiliser notre outil de dessin.
Vertical :
1. Milieu dans lequel le son a une vitesse d'environ 340 m/s.
2. Grandeur égale au rapport de la distance parcourue et de la durée du parcours. Elle s'exprime en m/s.
3. Se dit d'un milieu dans lequel le son peut se propager.
1. Milieu dans lequel le son a une vitesse d'environ 340 m/s.
2. Grandeur égale au rapport de la distance parcourue et de la durée du parcours. Elle s'exprime en m/s.
3. Se dit d'un milieu dans lequel le son peut se propager.
Horizontal :
4. Unité de longueur correspondant à la distance parcourue par la lumière en une année.
5. Milieu dans lequel la vitesse de la lumière est d'environ 300 000 km/s.
4. Unité de longueur correspondant à la distance parcourue par la lumière en une année.
5. Milieu dans lequel la vitesse de la lumière est d'environ 300 000 km/s.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je sais faire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7La lumière met environ quatre ans pour nous parvenir de l'étoile Proxima du Centaure. À quelle distance de la Terre est-elle située ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8La distance entre la Terre et l'étoile Rigel est estimée à 863 années-lumière. Combien de temps la lumière met-elle pour parcourir la distance entre Rigel et la Terre ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9La lumière met environ 1,28 s pour parcourir la distance Terre-Lune. À quelle distance de la Terre la Lune se situe-t-elle environ ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice corrigé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compétence : Pratiquer le calcul numérique et le calcul littéral
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10Télémétrie sonore.
Ben Underwood est un non-voyant qui a la capacité de détecter à distance la présence d'un obstacle sur son chemin. Son attention auditive est telle qu'il perçoit le léger décalage entre le moment où il produit un son (par exemple un claquement de la langue) et celui où l'écho lui revient. L'habitude lui permet de déduire de cette durée la distance à laquelle se trouve l'obstacle qui a généré l'écho. Supposons que Ben entende l'écho de son claquement de langue 47 ms après l'avoir émis.

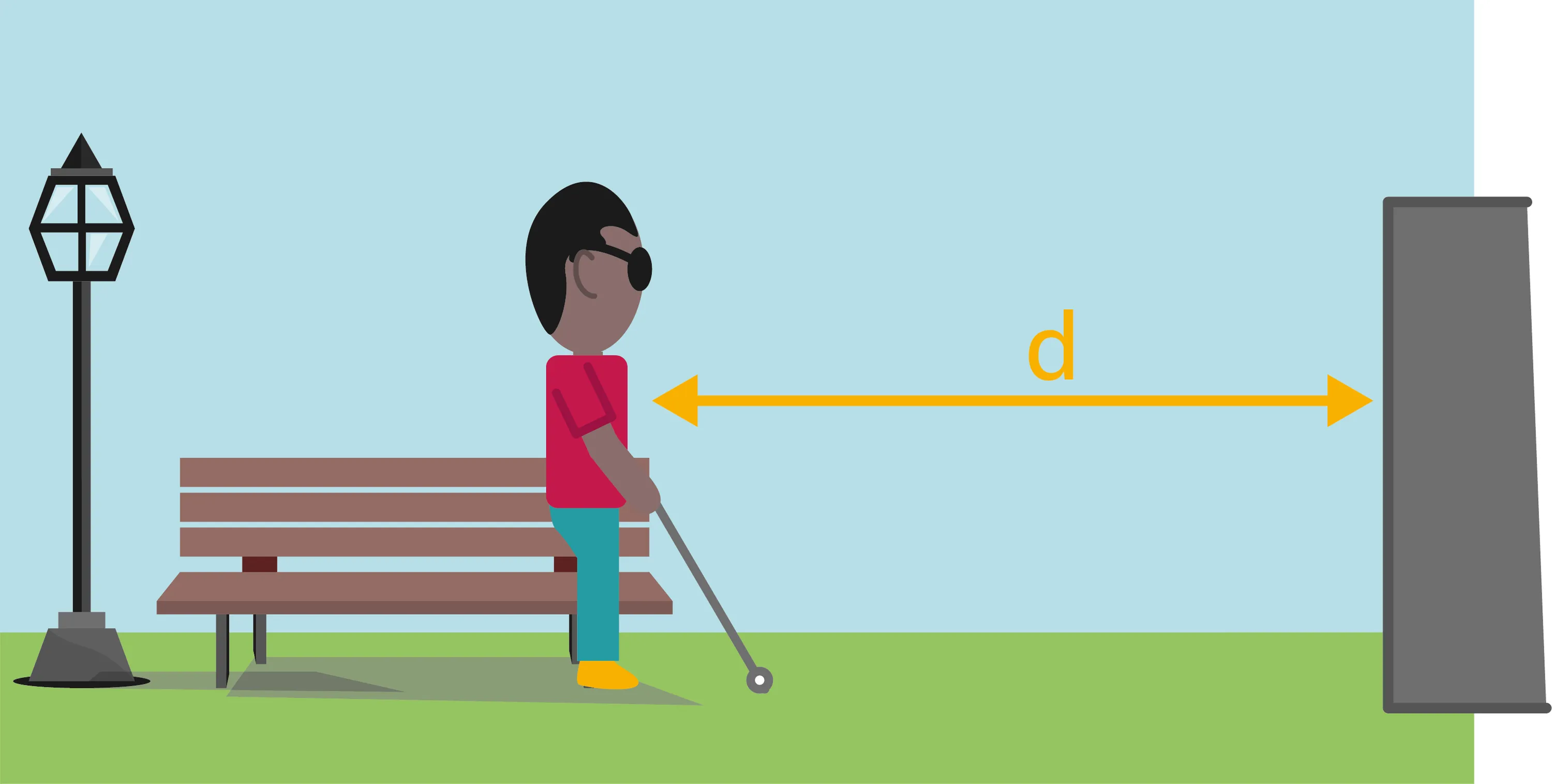
1. Convertis 47 ms en s.
2. Calcule en mètres la distance parcourue par ce son.
2. Calcule en mètres la distance parcourue par ce son.
3. Cette distance est-elle celle à laquelle l'obstacle se situe de Ben, sachant que le son fait un aller-retour entre lui et l'obstacle ?
4. Calcule en mètres la distance entre le non-voyant et l'obstacle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étapes de la méthode
- Pour convertir des millisecondes en secondes, on peut utiliser le tableau de conversion.
s ms
- Pour effectuer l'application numérique, on remplace la vitesse v (en m/s) et la durée du trajet t (en s) par leurs valeurs.
- Les sons parcourent la distance d entre Ben et l'objet puis de nouveau la distance d pour revenir de l'objet à Ben.
- Pour calculer la distance d, on divise la distance d' par le nombre de fois que les sons parcourent la distance d.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Corrigé
- 1 ms = 0,001 s donc 47 ms = 0,047 s.
- La vitesse du son dans l'air est de 340 m/s. En notant d' la distance demandée, on a la relation d' = v \times t. On peut donc calculer la distance d' parcourue par le son : d' = 3\:40 \times 0\text{,}047 = 16 m.
- Le son effectue un aller-retour. Il parcourt donc 2 fois la distane d à laquelle se trouve l'obstacle d'où d' = 2d.
- d' = 2d et donc d = \dfrac{d'}{2}.
D'où l'application numérique d = \dfrac{16}{2} = 8 m.
La distance entre Ben et l'obstacle est de 8 m.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice similaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11Télémétrie laser.
Le télémètre laser permet de mesurer des distances. Il mesure la durée nécessaire à la lumière pour faire l'aller-retour entre l'objet réflecteur et lui. Il calcule ensuite la distance qui les sépare. Soit une situation pour laquelle cette durée est de 0,1 μs.
Donnée : 1 μs = 0,000 001 en s.
Donnée : 1 μs = 0,000 001 en s.
1. Convertis 0,1 μs en s.
2. Calcule en mètres la distance qu'a parcourue cette lumière.
2. Calcule en mètres la distance qu'a parcourue cette lumière.
3. Cette distance est-elle celle à laquelle l'objet se situe du télémètre, sachant que la lumière fait un aller-retour entre lui et l'objet ?
4. Calcule la valeur en mètres de la distance entre le télémètre et l'objet.
4. Calcule la valeur en mètres de la distance entre le télémètre et l'objet.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je m'entraine
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12Grandeurs et unités.
1. Quelle relation existe-t-il entre la vitesse v, la distance d et la durée de parcours t ?
2. Quelles sont les unités respectives de v, d et t dans le Système international d'unités ?
2. Quelles sont les unités respectives de v, d et t dans le Système international d'unités ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13Unités de temps.
L'unité de durée dans le Système international d'unités est la seconde, mais on en utilise d'autres dans la vie quotidienne.
1. Combien y a-t-il de secondes dans une minute ?
2. Combien y a-t-il de minutes dans une heure ?
2. Combien y a-t-il de minutes dans une heure ?
3. Combien y a-t-il d'heures dans une journée ?
4. Combien y a-t-il de secondes dans une journée ?
4. Combien y a-t-il de secondes dans une journée ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14Conversions de longueurs.
Convertis les valeurs suivantes :
1. 1 a.l. = km.
2. 5,28 km = m.
3. 935 882 m = km.
2. 5,28 km =
3. 935 882 m =
4. 7,9 a.l. = km.
5. 0,3 a.l. = m.
6. 3 000 000 000 000 km = a.l.
5. 0,3 a.l. =
6. 3 000 000 000 000 km =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15L'année-lumière.
L'année-lumière est une unité utilisée pour exprimer les très grandes distances de l'Univers.
1. Quelle est la vitesse de la lumière dans le vide ?
2. Sachant qu'il y a 86 400 s dans une journée, calcule en kilomètres la distance à laquelle correspond une année-lumière.
1. Quelle est la vitesse de la lumière dans le vide ?
2. Sachant qu'il y a 86 400 s dans une journée, calcule en kilomètres la distance à laquelle correspond une année-lumière.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16Conversions de durée.
Convertis les valeurs suivantes :
1. 360 s = min.
2. 4,5 h = min.
3. 2 h = s.
4. 8 min 12 s = s.
5. 1 h 23 min = min.
6. 2 h 10 min = s.
1. 360 s =
2. 4,5 h =
3. 2 h =
4. 8 min 12 s =
5. 1 h 23 min =
6. 2 h 10 min =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17Vitesse du son.
Dans l'air, un son parcourt 20 400 m en une minute.
1. Rappelle la relation entre la vitesse, la distance parcourue et la durée du trajet.
2. Calcule la vitesse du son dans l'air en m/s.
1. Rappelle la relation entre la vitesse, la distance parcourue et la durée du trajet.
2. Calcule la vitesse du son dans l'air en m/s.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18Vitesse de la lumière.
Dans l'eau, la lumière se propage plus lentement que dans le vide : 225 000 km/s.
1. Rappelle la relation entre la vitesse, la distance parcourue et la durée du trajet.
2. Calcule la distance parcourue par la lumière dans l'eau en 20 ms.
1. Rappelle la relation entre la vitesse, la distance parcourue et la durée du trajet.
2. Calcule la distance parcourue par la lumière dans l'eau en 20 ms.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19Unités de vitesse.
Dans le tableau suivant, précise les unités de distance et de durée pour que le résultat du calcul v = \dfrac{d}{t} soit dans l'unité de vitesse indiquée.
| Vitesse | Distance | Unité de distance | Temps | Unité de temps |
| 50 m/s | 200 |
| 4 |
|
| 78 km/h | 202,8 |
| 2,6 |
|
| 678 km/s | 2 779,8 |
| 4,1 |
|
| 45 cm/s | 90 |
| 2 |
|
| 37 827 m/h | 245 875,5 |
| 6,5 |
|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20Utiliser les puissances de 10.
✔︎ Compétence : Présenter mon résultat avec l'unité adaptée
La Terre est située à environ 1,5 x 108 km du Soleil. Cette distance a été choisie pour définir l'unité astronomique U.A. 1 U. A. = 1,5 x 108 km.
1. L'étoile Rigel est située à environ 860 a.l. de la Terre. Calcule la distance entre la Terre et Rigel en U.A.
2. Pour quelle raison l'année-lumière est-elle l'unité la plus adaptée pour exprimer cette distance ?
La Terre est située à environ 1,5 x 108 km du Soleil. Cette distance a été choisie pour définir l'unité astronomique U.A. 1 U. A. = 1,5 x 108 km.
1. L'étoile Rigel est située à environ 860 a.l. de la Terre. Calcule la distance entre la Terre et Rigel en U.A.
2. Pour quelle raison l'année-lumière est-elle l'unité la plus adaptée pour exprimer cette distance ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une notion, trois exercices
Différenciation
Compétence : Conclure, valider ou non l'hypothèse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21-ADes feux d'artifice
Comme pour l'orage, pour savoir à quelle distance un feu d'artifice explose, on compte le nombre de secondes qui séparent la vision de l'explosion et son bruit puis on divise ce nombre par 3 : on obtient alors, en km, la distance qui nous sépare de l'explosion. Vérifions la validité de ce calcul avec un exemple. Une fusée explose à 4 km d'un observateur. La lumière se propage à 300 000 km/s, le son se propage à 340 m/s.
1. Rappelle la relation mathématique qui permet de calculer la vitesse de propagation v en fonction de la distance d parcourue pendant une durée t.
2. Déduis-en la relation mathématique qui permet de relier la durée t à la distance d et la vitesse de propagation v.
3. Identifie et recopie les valeurs des vitesses vlumière et vson, et de la distance d. Écris-les sous la forme vlumière … ; vson … ; d = ... .
4. Calcule la durée du trajet de la lumière de l'explosion jusqu'à l'observateur.
2. Déduis-en la relation mathématique qui permet de relier la durée t à la distance d et la vitesse de propagation v.
3. Identifie et recopie les valeurs des vitesses vlumière et vson, et de la distance d. Écris-les sous la forme vlumière … ; vson … ; d = ... .
4. Calcule la durée du trajet de la lumière de l'explosion jusqu'à l'observateur.
5. Calcule la durée du trajet du son de l'explosion jusqu'à l'observateur.
6. Calcule la différence de durée entre tson et tlumière. Ce résultat est-il très différent de tson ?
7. Calcule la distance que l'on obtiendrait avec cette durée par la méthode de la division par 3, puis indique si cette méthode te parait acceptable.
6. Calcule la différence de durée entre tson et tlumière. Ce résultat est-il très différent de tson ?
7. Calcule la distance que l'on obtiendrait avec cette durée par la méthode de la division par 3, puis indique si cette méthode te parait acceptable.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21-BLe sémaphore
Le sémaphore est un moyen de communication inventé à la fin du XVIIIe siècle par les frères Chappe. Il consiste en une suite de relais placés les uns après les autres. Les messages sont transmis par le biais de symboles formés par une structure au sommet d'une tour. En 1792, la première ligne de sémaphores permet de transmettre le premier symbole d'un message en 9 minutes (540 secondes) sur une distance de 193 km par l'intermédiaire de 15 postes-relais. La lumière se propage à 300 000 km/s, le son se propage à 340 m/s.


1. Rappelle la relation mathématique qui permet de calculer la durée du trajet t en connaissant la distance d et la vitesse de propagation v.
2. Calcule la durée tson que mettrait le son à parcourir cette distance.
3. Calcule la durée tlumière que mettrait la lumière à parcourir cette distance.
2. Calcule la durée tson que mettrait le son à parcourir cette distance.
3. Calcule la durée tlumière que mettrait la lumière à parcourir cette distance.
4. Compare la durée de propagation du symbole à celle du son.
5. Formule une hypothèse pour expliquer le fait que la durée de propagation du symbole est inférieure à celle du son.
5. Formule une hypothèse pour expliquer le fait que la durée de propagation du symbole est inférieure à celle du son.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21-CLa foudre et le tonnerre
Pour estimer en kilomètres la distance à laquelle la foudre tombe de notre position, on compte le nombre de secondes qui séparent la vision de l'éclair et le bruit du tonnerre puis on divise ce nombre par 3. On obtient alors en kilomètres la distance à laquelle est l'orage. Vérifions la validité de cette méthode. La foudre est tombée à 3 km d'un observateur qui a compté 9 s avant d'entendre le tonnerre. On rappelle que la lumière se propage à 300 000 km/s, tandis que le son se propage à 340 m/s.


1. Calcule la différence entre les durées mises par la lumière et le son du tonnerre pour parcourir 3 km.
2. En utilisant la méthode de la division par 3, quelle distance l'observateur va-t-il trouver pour l'orage ? La méthode de la division par 3 est-elle valide dans ce cas ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
J'approfondis
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22Attends-moi !
Enzo et Bilal font une balade en vélo. Enzo a pris un peu d'avance. Bilal crie pour qu'il l'attende. Le son de la voix de Bilal met 2 s pour atteindre Enzo.
1. Quelle est la valeur moyenne de la vitesse du son dans l'air ?
2. Calcule la distance qui sépare Enzo et Bilal.
1. Quelle est la valeur moyenne de la vitesse du son dans l'air ?
2. Calcule la distance qui sépare Enzo et Bilal.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23Le mur du son.
Lorsqu'un avion vole à une vitesse supérieure à la vitesse du son dans l'air, on dit qu' « il franchit le mur du son ». On entend alors un bang supersonique.
1. À quelle vitesse minimale en m/s l'avion doit-il voler pour franchir le mur du son dans l'air ?
2. Quelle distance en mètres l'avion parcourt-il en 1 h à cette vitesse ?
2. Quelle distance en mètres l'avion parcourt-il en 1 h à cette vitesse ?
3. Convertis cette distance en km.
4. Déduis-en la vitesse minimale en km/h d'un avion en vol supersonique.
4. Déduis-en la vitesse minimale en km/h d'un avion en vol supersonique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24Sirius..
L'étoile Sirius est l'étoile la plus brillante lorsqu'on observe le ciel. Elle est située à environ 86 000 000 000 000 km de la Terre.
1. À combien d'années-lumière Sirius est-elle située de la Terre ?
2. Quelle durée la lumière de Sirius met-elle pour nous parvenir ?
1. À combien d'années-lumière Sirius est-elle située de la Terre ?
2. Quelle durée la lumière de Sirius met-elle pour nous parvenir ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Jupiter.
Jupiter peut être confondue avec une étoile lorsqu'on observe le ciel nocturne à l'œil nu. Pourtant, il s'agit bien d'une planète qui nous renvoie la lumière du Soleil. La distance maximale entre la Terre et Jupiter est d'environ 965 000 000 km.
1. Quelle durée en minutes la lumière met-elle pour nous parvenir de Jupiter ?
2. Calcule la distance entre la Terre et Jupiter en années-lumière.
3. L'année-lumière te semble-t-elle être une unité bien adaptée pour exprimer la distance entre la Terre et Jupiter ?
1. Quelle durée en minutes la lumière met-elle pour nous parvenir de Jupiter ?
2. Calcule la distance entre la Terre et Jupiter en années-lumière.
3. L'année-lumière te semble-t-elle être une unité bien adaptée pour exprimer la distance entre la Terre et Jupiter ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26Mesure de la distance Terre-Lune.
Lors des missions Apollo et Lunokhod, des réflecteurs ont été déposés à la surface de la Lune. Ils permettent de déterminer la distance Terre-Lune en dirigeant un faisceau laser sur eux. L'expérience est réalisée, entre autres, à l'observatoire de la Côte d'Azur.
1. Rappelle la valeur de la vitesse de la lumière dans le vide.
2. La durée nécessaire à la lumière pour effectuer l'aller-retour Terre-Lune est en moyenne de 2,5 s. Calcule la distance parcourue par la lumière puis la distance Terre-Lune.
1. Rappelle la valeur de la vitesse de la lumière dans le vide.
2. La durée nécessaire à la lumière pour effectuer l'aller-retour Terre-Lune est en moyenne de 2,5 s. Calcule la distance parcourue par la lumière puis la distance Terre-Lune.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27Exoplanète.
Une exoplanète est une planète située en dehors de notre système solaire, en orbite autour d'une étoile autre que le Soleil.
La planète Kepler-438b est située à 470 a.l. de la Terre.
1. Combien d'années faudrait-il pour se rendre sur Kepler-438b depuis la Terre en voyageant à la vitesse de la lumière ?
2. Quelle est la distance en kilomètres séparant la Terre de Kepler-438 b ?
1. Combien d'années faudrait-il pour se rendre sur Kepler-438b depuis la Terre en voyageant à la vitesse de la lumière ?
2. Quelle est la distance en kilomètres séparant la Terre de Kepler-438 b ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Parsec.
Les astronomes ont une autre unité à leur disposition, pour exprimer les très grandes distances de l'Univers. Cette unité est le parsec. Son nom vient de la méthode de mesure historiquement utilisée pour déterminer les distances entre la Terre et les astres lointains étudiés.
1 parsec (pc) vaut environ 3,26 années-lumière.
1. L'étoile Proxima du Centaure est située à 4,22 a.l. de la Terre. Convertis cette distance en parsecs.
2. Rappelle la valeur d'une année-lumière en kilomètres.
3. Exprime un parsec en kilomètres.
1. L'étoile Proxima du Centaure est située à 4,22 a.l. de la Terre. Convertis cette distance en parsecs.
2. Rappelle la valeur d'une année-lumière en kilomètres.
3. Exprime un parsec en kilomètres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29Astronomique !
Lorsque les astronomes ont commencé à étudier le système solaire, ils ont utilisé une unité adaptée à l'expression des distances rencontrées : l'unité astronomique (notée U.A.). Une unité astronomique est égale à la distance Terre-Soleil.
Donnée : distance maximale entre la Terre et Jupiter d = 965 000 000 km
1. Sachant que la lumière met 8 min 12 s pour parcourir la distance Terre-Soleil, calcule la valeur d'une unité astronomique en mètres.
2. Convertis cette valeur en kilomètres.
3. Exprime la distance maximale entre la Terre et Jupiter en U.A.
Donnée : distance maximale entre la Terre et Jupiter d = 965 000 000 km
1. Sachant que la lumière met 8 min 12 s pour parcourir la distance Terre-Soleil, calcule la valeur d'une unité astronomique en mètres.
2. Convertis cette valeur en kilomètres.
3. Exprime la distance maximale entre la Terre et Jupiter en U.A.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30Sonar.
Joachim accompagne son père, pêcheur, sur son bateau qui est équipé d'un sonar. C'est un dispositif utilisé pour repérer les bancs de poissons. Le sonar émet un son dans l'eau qui se réfléchit sur le banc de poissons puis repart vers le dispositif. La mesure de la durée du trajet du son permet de calculer la distance entre le bateau et le banc de poissons. Ce jour-là sur le bateau du père de Joachim, la durée mesurée est de 5 ms.
Donnée : vitesse du son dans l'eau 1 500 m/s.
1. Convertis cette durée en s.
2. Calcule la distance parcourue par le son pour effectuer l'aller-retour entre le sonar et le banc de poissons
3. Calcule la distance entre le bateau et les poissons.
Donnée : vitesse du son dans l'eau 1 500 m/s.
1. Convertis cette durée en s.
2. Calcule la distance parcourue par le son pour effectuer l'aller-retour entre le sonar et le banc de poissons
3. Calcule la distance entre le bateau et les poissons.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31Feux d'artifice.
Le soir du 14 juillet, Kelly a décidé de regarder les feux d'artifice de chez elle. Malgré la colline qui sépare sa maison du stade d'où sont tirés les feux, elle peut en voir la plus grande partie.
1. Kelly constate que la détonation des feux d'artifice lui parvient 4 s après qu'elle a vu la lumière. On considère que les feux sont tirés à la verticale du stade. Calcule en km la distance entre le stade et la maison de Kelly.
2. À un moment, Kelly ne voit pas de lumière mais entend le crépitement des feux. Elle suppose que ce sont des feux qui tourbillonnent au niveau du sol. Pourquoi Kelly ne peut-elle plus voir les feux d'artifice à ce moment-là ?
1. Kelly constate que la détonation des feux d'artifice lui parvient 4 s après qu'elle a vu la lumière. On considère que les feux sont tirés à la verticale du stade. Calcule en km la distance entre le stade et la maison de Kelly.
2. À un moment, Kelly ne voit pas de lumière mais entend le crépitement des feux. Elle suppose que ce sont des feux qui tourbillonnent au niveau du sol. Pourquoi Kelly ne peut-elle plus voir les feux d'artifice à ce moment-là ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32Proxima b.
Proxima b est la planète la plus proche de la Terre en dehors de notre système solaire. Cette planète est remarquable car elle se trouve dans la zone habitable de l'étoile autour de laquelle elle gravite. Proxima b est située à 4,2 a.l. de la Terre. La vitesse maximale d'une navette spatiale est actuellement d'environ 28 000 km/h.
1. Calcule en km la distance entre la Terre et Proxima b, en utilisant les puissances de 10.
2. Combien d'années faudrait-il actuellement à une navette spatiale pour aller de la Terre à Proxima b si elle pouvait maintenir sa vitesse maximale tout au long du trajet ?
1. Calcule en km la distance entre la Terre et Proxima b, en utilisant les puissances de 10.
2. Combien d'années faudrait-il actuellement à une navette spatiale pour aller de la Terre à Proxima b si elle pouvait maintenir sa vitesse maximale tout au long du trajet ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33Fibre optique.
L'utilisation d'internet nécessite des flux de données de plus en plus importants. La fibre optique est en cours de déploiement dans de nombreuses villes. Une fibre optique est constituée de plusieurs couches. Au centre, on trouve un tube de verre très fin dans lequel se propage le signal lumineux.
Données : vitesse de la lumière dans le verre de la fibre optique = 200 000 km/s ; distance entre Paris et Lyon : environ 470 km.
1. Calcule la durée nécessaire à un signal pour être transmis par fibre optique de Paris à Lyon.
2. Un courriel met environ 10 secondes pour être transmis entre deux utilisateurs situés respectivement à Paris et à Lyon. a. Compare cette durée à celle de la transmission du signal calculée à la question précédente. b. La durée de transmission des informations est-elle limitée par celle du traitement des données ou par celle de la transmission du signal ?
Données : vitesse de la lumière dans le verre de la fibre optique = 200 000 km/s ; distance entre Paris et Lyon : environ 470 km.
1. Calcule la durée nécessaire à un signal pour être transmis par fibre optique de Paris à Lyon.
2. Un courriel met environ 10 secondes pour être transmis entre deux utilisateurs situés respectivement à Paris et à Lyon. a. Compare cette durée à celle de la transmission du signal calculée à la question précédente. b. La durée de transmission des informations est-elle limitée par celle du traitement des données ou par celle de la transmission du signal ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je résous un problème
Compétence : Lire et comprendre des documents scientifiques pour en extraire des informations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1 Écholocation des dauphins.
Les dauphins sont des mammifères de la famille des cétacés. Ils sont capables d'émettre et de capter des sons afin de sonder leur environnement : c'est l'écholocation. Cela leur permet de localiser leurs proies. Les dauphins n'émettent pas les sons en continu mais par salves, c'est-à-dire pendant un bref instant et plusieurs fois de suite à intervalles de temps réguliers. Le temps entre chaque émission et la durée de la salve dépendent de la situation (chasse ou localisation).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
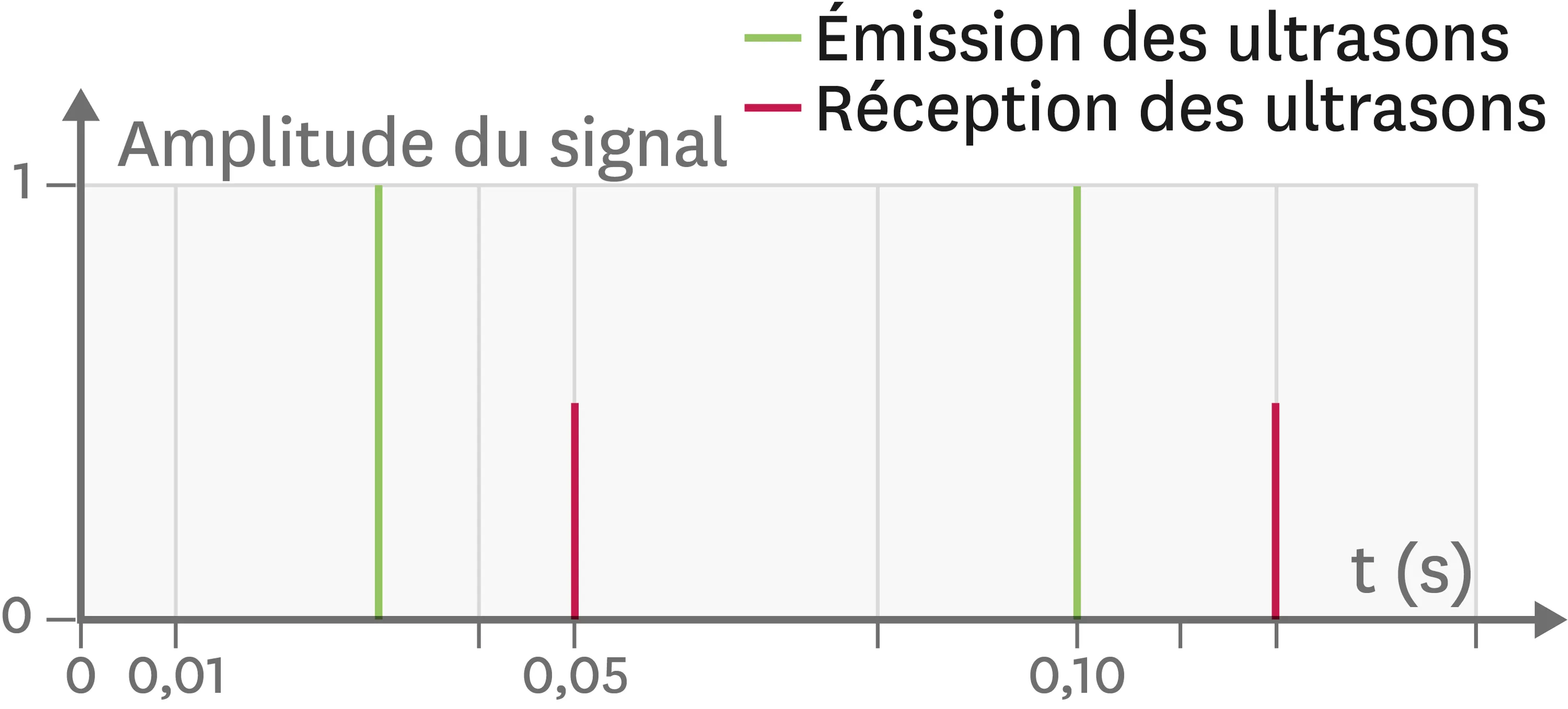
Doc. 2Émission et réception des sons par un dauphin.
L'émission de la salve est repérée en vert, la réception est repérée en rouge. On peut donc lire sur le graphique la durée du trajet des ultrasons.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les dauphins utilisent l'écholocation pour se repérer dans leur milieu aquatique. Détermine à quelle distance du fond se trouve un dauphin, sachant que le son se déplace à environ 1 500 m/s dans l'eau.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices supplémentaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34Conversions de longueurs.
Convertis les valeurs suivantes en utilisant les puissances 10 :
1. 1 a.l. = km.
2. 5,28 km = m.
3. 935 882 m = km.
4. 7,9 a.l. = km.
2. 5,28 km =
3. 935 882 m =
4. 7,9 a.l. =
5. 0,3 a.l. = m.
6. 3 000 000 000 000 km = a.l.
7. 4,3 a.l. = km.
8. 21 a.l. = km.
6. 3 000 000 000 000 km =
7. 4,3 a.l. =
8. 21 a.l. =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35Déterminer une vitesse.
Un TGV parcourt la distance entre Paris et Lyon, soit environ 460 km, en environ 2 h.
1. Calcule la vitesse moyenne du TGV sur ce trajet.
2. Combien de temps (en heures) faudrait-il à ce TGV pour parcourir les 640 km séparant Lyon de Barcelone ?
1. Calcule la vitesse moyenne du TGV sur ce trajet.
2. Combien de temps (en heures) faudrait-il à ce TGV pour parcourir les 640 km séparant Lyon de Barcelone ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36Des mots pour une phrase.
Utilise les mots dans l'ordre que tu souhaites pour construire des phrases correctes.
1. son / propager / matériel ;
2. vitesse / unité / système international ;
2. vitesse / unité / système international ;
3. unité / distances / univers ;
4. lumière / distances / informations.
4. lumière / distances / informations.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Parcours de compétences
Compétence : Émettre des hypothèses
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Un 14 juillet, à la tombée du jour, un pilote de chasse curieux passe au-dessus du site d'un feu d'artifice. Une bombe d'artifice éclate juste derrière son avion. Son supérieur lui reproche par radio de prendre des risques, mais le pilote estime qu'il n'était pas si proche, car bien qu'ayant vu l'éclat il n'a pas entendu la bombe.
Quelle hypothèse permet d'expliquer que le pilote n'a pas entendu le son de la détonation ?
Quelle hypothèse permet d'expliquer que le pilote n'a pas entendu le son de la détonation ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 1
Je sais ce qu'est une hypothèse.
Coup de pouce
Pourquoi le supérieur a-t-il fait des reproches au pilote ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 2
Je repère les éléments en lien avec le schéma.
Coup de pouce
Pour expliquer qu'il n'a pas entendu l'explosion, quelle hypothèse le pilote fait-il à propos du niveau sonore perçu et de la distance entre l'émetteur et le récepteur du son ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 3
Je propose une hypothèse en lien avec le problème.
Coup de pouce
Propose une hypothèse impliquant le fait que l'avion se déplace pour expliquer que le pilote n'ait pas entendu l'explosion tout en étant très proche d'elle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 4
Je formule clairement l'hypothèse que j'ai émise pour me permettre de la valider.
Coup de pouce
Utilise la comparaison de la vitesse d'un signal avec celle du récepteur de ce signal pour proposer une explication aux observations du pilote.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

