Chapitre 11
Fiche de révision
Description d'un mouvement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Schémas
Téléchargez ce bilan en format pdf .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Grandeurs physiques
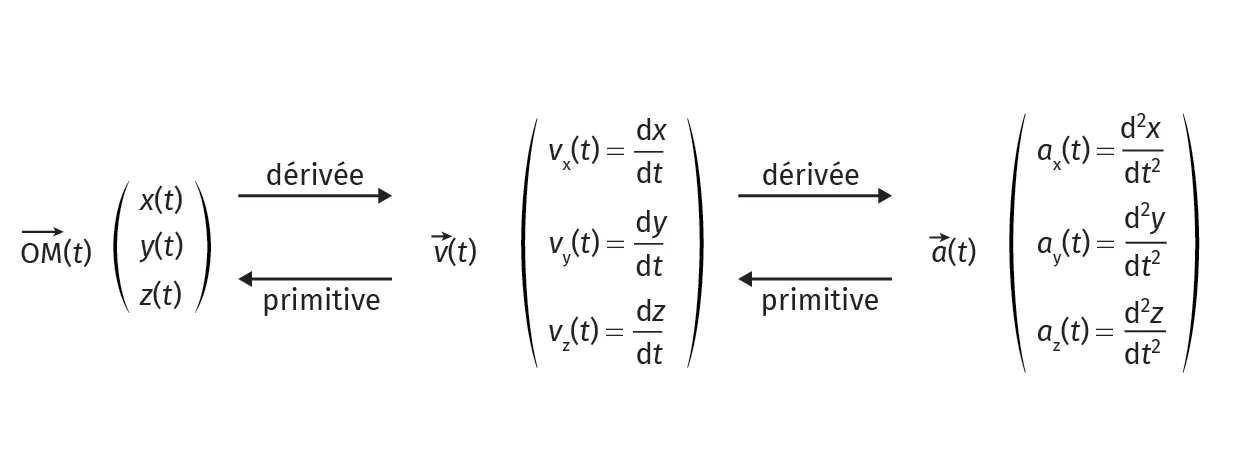
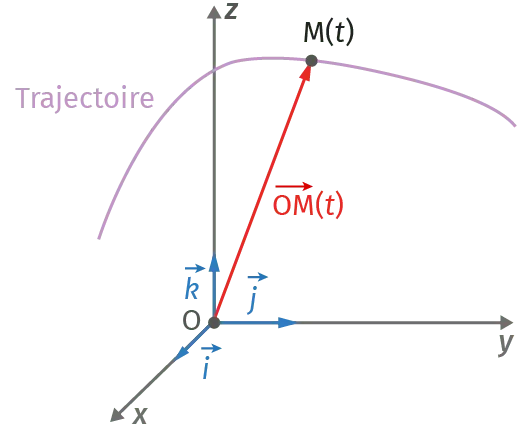
- En coordonnées cartésiennes, dans la base (O, \vec{i}, \vec{j}, \vec{k}) :
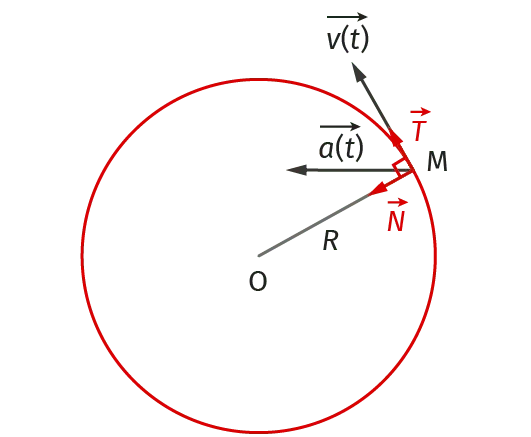
- Dans le repère de Frenet, centré sur \text{M} :
\vec{v} = v \cdot \overrightarrow{T} soit \vec{v} \dbinom{v}{0}_{(\text{M, } \overrightarrow{T},\ \overrightarrow{N})} le vecteur vitesse est toujours tangent à la trajectoire.
\vec{a} = \dfrac{\text{d}v}{\text{d}t} \cdot \overrightarrow{T} + \dfrac{v^2}{R} \cdot \overrightarrow{N} soit \vec{a} \begin{pmatrix} \dfrac{\text{d}v}{\text{d}t} \\ \dfrac{v^2}{R} \end{pmatrix}_{(\text{M, } \overrightarrow{T},\ \overrightarrow{N})} le vecteur accélération est toujours dirigé vers l'intérieur de la courbure de la trajectoire.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Mouvements particuliers à connaître
- Mouvement rectiligne uniforme selon l'axe (\text{O}x) :
- \vec{a}(t) = \vec{0}
- \vec{v}(t) = v \cdot \vec{i}
- \overrightarrow{\text{OM}}(t) = (v \cdot t + x_0) \cdot \vec{i}
- Mouvement rectiligne uniformément accéléré selon l'axe (\text{O}x) :
- \vec{a}(t) = a \cdot \vec{i}
- \vec{v}(t) = (a \cdot t + v_0) \cdot \vec{i}
- \overrightarrow{\text{OM}}(t) = \left(\dfrac{a}{2} \cdot t^2 + v_0 \cdot t + x_0\right) \cdot \vec{i}
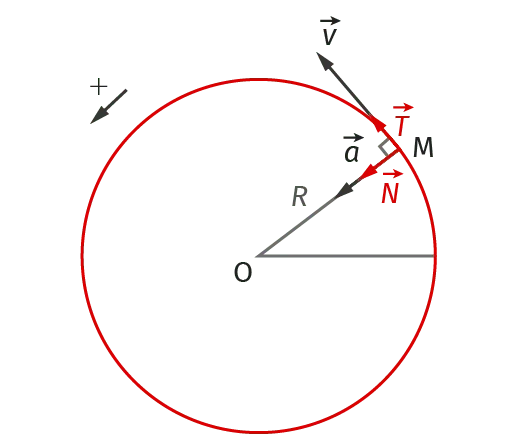
- Mouvement circulaire uniforme dans le repère de Frenet (\text{M}, \overrightarrow{T}, \overrightarrow{N}) :
- \vec{v} = v \cdot \overrightarrow{T} : le vecteur vitesse est toujours tangent à la trajectoire.
- \vec{a} = \dfrac{v^2}{R} \cdot \overrightarrow{N}

Fermer
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

