Chapitre 16
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39Des triangles rectangles
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
✔ Je décompose un problème en sous-problèmes pour le simplifier et le résoudre
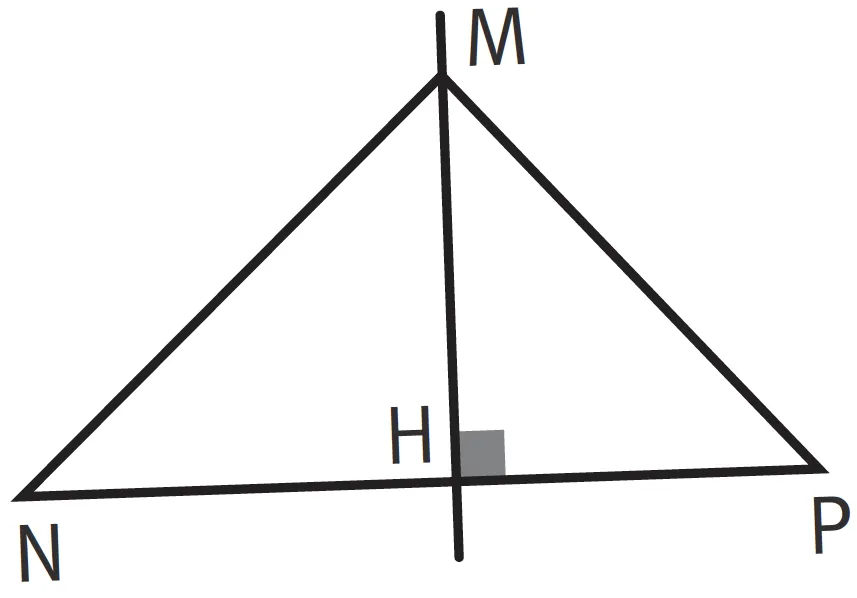Les triangles MHP et MNH sont rectangles en H, les points N, H et P sont alignés, MN = 1,5 cm ; NH = 0,9 cm et HP = 1,6 cm.
Calculez l'aire du triangle MNP.
✔ Je décompose un problème en sous-problèmes pour le simplifier et le résoudre
Calculez l'aire du triangle MNP.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Pour calculer l'aire du triangle, on détermine la longueur d'une hauteur et celle de la base correspondante, puis on utilise la formule de l'aire d'un triangle quelconque.
Corrigé 1
- \text{NP} = 0\text{,}9 + 1\text{,}6 = 2\text{,}5
[NP] mesure 2,5 cm. - Dans le triangle MNH rectangle en H, on applique le théorème de Pythagore :
\text{MN}^2 = \text{NH}^2 + \text{MH}^2
1\text{,}52 = 0\text{,}9^2 + \text{MH}^2
2\text{,}25 = 0\text{,}81 + \text{MH}^2
\text{MN}^2 = 2\text{,}25 - 0\text{,}81
\text{MN}^2 = 1\text{,}44
\text{MN} = \sqrt{1\text{,}44}
\text{MN} = 1\text{,}2
- A_{\text{MNP}} = \text{NP} \times \text{MH} \div 2 = 2,5 \times 1,2 \div 2 = 1\text{,}5
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Pour calculer l'aire d'un triangle, on démontre qu'il est rectangle à l'aide de la réciproque du théorème de Pythagore. On peut ensuite déterminer son aire avec la formule de l'aire d'un triangle rectangle.
D'après la réciproque du théorème de Pythagore, le triangle MNP est rectangle en M.
Corrigé 2
- Dans le triangle MHP rectangle en H, on applique le théorème de Pythagore :
\text{MP}^2 = \text{HP}^2 + \text{MH}^2
\text{MP}^2 =1\text{,}6^2 + 1\text{,}2^2
\text{MP}^2 = 2\text{,}56 + 1\text{,}44
\text{MP}^2 = 4
\text{MP} = \sqrt{4}
\text{MP} = 2
- Dans le triangle MNP, [NP] est le plus grand côté et {\text{NP}^2 = (\text{NH} + \text{HP})^2}
\text{NP}^2 = (0\text{,}9 + 1,6)^2
\text{MP}^2 = 2\text{,}5^2
\text{MP}^2 = 6\text{,}25
et \text{MP}^2 + \text{MN}^2 = 4 + 2\text{,}25 = 6\text{,}25
D'après la réciproque du théorème de Pythagore, le triangle MNP est rectangle en M.
- A_{\text{MNP}} = \text{MN} \times \text{MP} \div 2
= 1\text{,}5 \times 2 \div 2
= 1\text{,}5
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40Problème similaireLʼaire dʼun losange
✔ Je structure mon raisonnement
Le côté du losange IJKL mesure 5 cm et sa diagonale [IK] mesure 4,2 cm.
Calculez l'aire du losange.
Le côté du losange IJKL mesure 5 cm et sa diagonale [IK] mesure 4,2 cm.
Fermer
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
