Chapitre 13
Entrée en matière
Angles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des mathsLa trisection de l'angle
L'étude des angles est aussi ancienne que la géométrie elle-même.
Les scientifiques babyloniens, égyptiens et grecs les ont étudiés
durant des siècles.
Cependant, un problème bien particulier, connu dès l'Antiquité, a persisté jusque très tard dans l'histoire : la trisection de l'angle. Ce problème consiste à partager un angle quelconque en trois angles de même mesure en utilisant uniquement la règle et le compas.
Il a fallu attendre 1837, soit près de deux millénaires après la formulation du problème, pour que le mathématicien français Pierre-Laurent Wantzel démontre que cette construction est tout simplement impossible !
Cependant, un problème bien particulier, connu dès l'Antiquité, a persisté jusque très tard dans l'histoire : la trisection de l'angle. Ce problème consiste à partager un angle quelconque en trois angles de même mesure en utilisant uniquement la règle et le compas.
Il a fallu attendre 1837, soit près de deux millénaires après la formulation du problème, pour que le mathématicien français Pierre-Laurent Wantzel démontre que cette construction est tout simplement impossible !

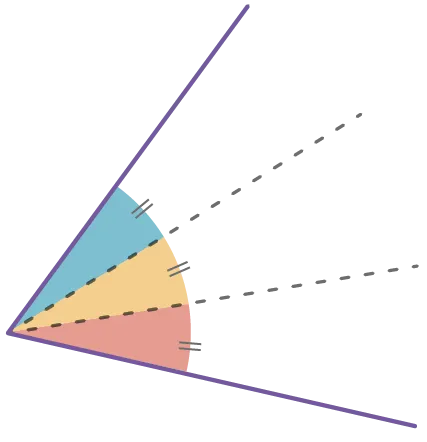
La trisection d'un angle : l'angle est divisé en trois angles égaux.
Uniquement à la règle et au compas, diviser un angle quelconque en deux angles
égaux, puis en quatre angles égaux.
Cliquez pour accéder à GeoGebra
Supplément numérique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les maths, à quoi ça sert ?
Le mot « angle » est très utilisé dans le langage courant : angle de tir au rugby, angle de
coupe en menuiserie, angle mort pour les conducteurs, grand angle en photographie,
etc.
En arts par exemple, on peut jouer avec l'angle de vue. Une des techniques pour cela est l'anamorphose : le dessin paraît déformé mais, lorsqu'on le regarde sous un certain angle, il apparaît correctement. Cela permet de cacher un objet, comme dans le célèbre tableau Les Ambassadeurs de Hans Holbein. Mais cela peut aussi permettre de le révéler au public visé : c'est le cas des publicités sur les stades de football qui sont illisibles pour les joueurs mais correctement visibles pour les téléspectateurs.
En arts par exemple, on peut jouer avec l'angle de vue. Une des techniques pour cela est l'anamorphose : le dessin paraît déformé mais, lorsqu'on le regarde sous un certain angle, il apparaît correctement. Cela permet de cacher un objet, comme dans le célèbre tableau Les Ambassadeurs de Hans Holbein. Mais cela peut aussi permettre de le révéler au public visé : c'est le cas des publicités sur les stades de football qui sont illisibles pour les joueurs mais correctement visibles pour les téléspectateurs.

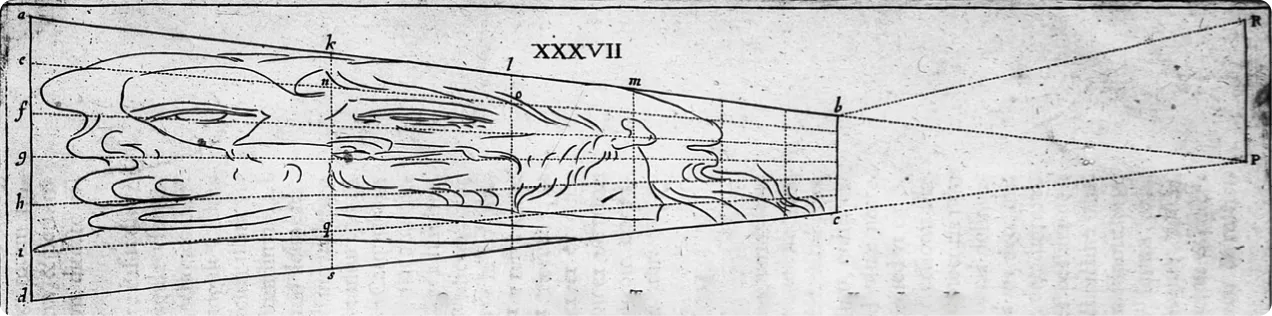
Dessin en anamorphose
Observer le dessin ci-dessus avec le bon angle de vue
pour voir le personnage non déformé.
Supplément numérique
Visualiser .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationTravailler avec des gabarits d'angle
Pour réaliser cette activité, utiliser la .
Ce travail est à réaliser en groupe afin de pouvoir utiliser plusieurs gabarits de même taille.
Lorsque l'on demande de mettre deux gabarits côte à côte, il faut que l'arc de cercle d'un gabarit prolonge l'arc de cercle de l'autre gabarit et que deux des côtés soient parfaitement accolés l'un à l'autre.
Ce travail est à réaliser en groupe afin de pouvoir utiliser plusieurs gabarits de même taille.
Lorsque l'on demande de mettre deux gabarits côte à côte, il faut que l'arc de cercle d'un gabarit prolonge l'arc de cercle de l'autre gabarit et que deux des côtés soient parfaitement accolés l'un à l'autre.

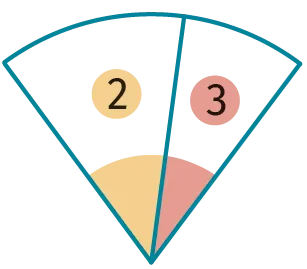
1. Comment s'appelle l'angle défini par le gabarit 1 ?
2. Lorsque l'on met côte à côte deux gabarits 1, on obtient un angle plat. Avec plusieurs
gabarits identiques, réaliser d'autres angles plats.
3. a. En utilisant plusieurs gabarits, réaliser un angle droit.
b. Est-il possible de faire un angle droit en utilisant le gabarit 4 ? Pourquoi ?
4. a. On souhaite former un cercle complet : combien faut-il de gabarits 1 pour ça ?
De gabarits 3 ? Et de gabarits 6 ?
b. Peut-on le faire avec des gabarits 5 ?
Cliquez pour accéder à GeoGebra
Cliquez pour accéder à GeoGebra
Bilan
Comment obtenir un angle plat à partir de l'angle droit ? Quel type d'angle obtient-on avec quatre angles droits ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationFabrication d'un rapporteur
Pour réaliser cette activité, utiliser la .
Le but de cette activité est de construire un rapporteur sur le grand demi-disque. Au cours de l'activité, tous les pliages doivent être faits sur le petit demi-disque, qu'on appelle gabarit.
1. Plier deux fois le gabarit en deux en superposant les coins. Bien marquer les plis, puis déplier.
2. On rappelle que l'angle plat a pour mesure 180^\circ. Quelles sont les mesures des angles formés par les plis ? Reporter ces angles sur le cercle intérieur du rapporteur et y indiquer leurs mesures.
3.
Plier le gabarit en amenant le coin gauche au centre du demi-cercle. Marquer le pli et
déplier. Noter \text {A} le point où le pli atteint le bord du demi-cercle. Plier le gabarit le long du
segment \text {[OA]} . On obtient un angle de 60^\circ. Comment obtenir 30^\circ ?
Le but de cette activité est de construire un rapporteur sur le grand demi-disque. Au cours de l'activité, tous les pliages doivent être faits sur le petit demi-disque, qu'on appelle gabarit.
1. Plier deux fois le gabarit en deux en superposant les coins. Bien marquer les plis, puis déplier.
2. On rappelle que l'angle plat a pour mesure 180^\circ. Quelles sont les mesures des angles formés par les plis ? Reporter ces angles sur le cercle intérieur du rapporteur et y indiquer leurs mesures.

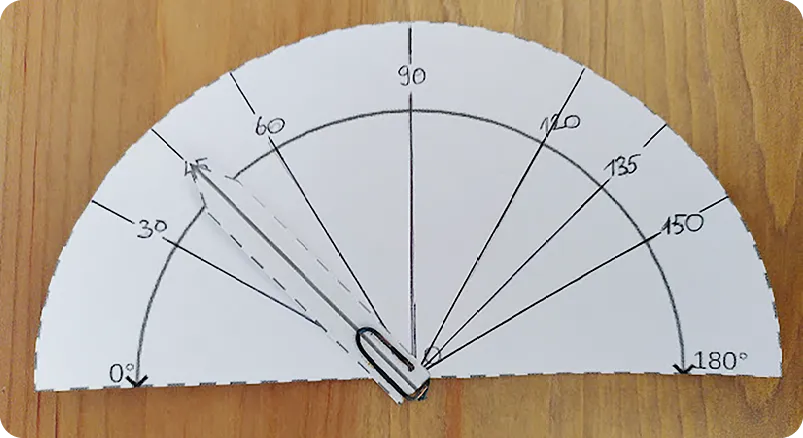
4. Placer les graduations 60^\circ, 120^\circ, 30^\circ et 150^\circ sur le rapporteur.
Bilan
En utilisant ce rapporteur, construire sur une feuille un premier angle qui mesure 30^\circ, un deuxième angle qui mesure 45^\circ et enfin un troisième angle qui mesure 75^\circ.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


