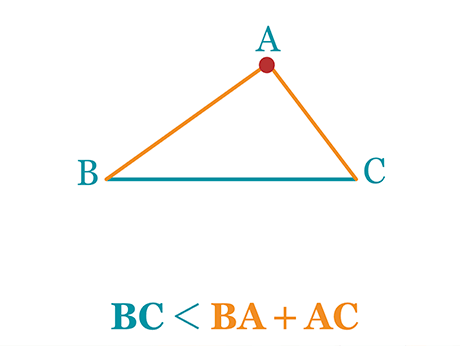Chapitre 16
Cours
Triangles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Généralités sur les triangles
Définition
Un triangle est un polygone à trois côtés qui possède donc trois angles.
Propriété : inégalité triangulaire
Dans un triangle \mathrm{ABC} non plat, on a les inégalités suivantes :
1. \mathrm{AB} < \mathrm{AC}+\mathrm{CB}
2. \mathrm{AC} < \mathrm{AB}+\mathrm{BC}
3. \mathrm{BC} < \mathrm{BA}+\mathrm{AC}
Version interactive
Propriété
Un triangle est constructible lorsque la longueur de son plus grand côté est strictement inférieure à la somme des longueurs des deux autres côtés.
Propriété
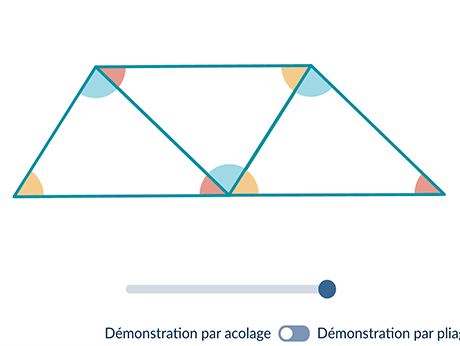
Dans un triangle, la somme des angles est égale à 180°. Les trois angles d'un triangle sont donc supplémentaires.
Exemple :

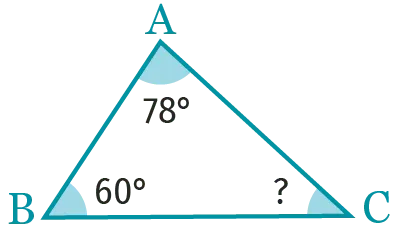
On a \widehat{\mathrm{ABC}}+\widehat{\mathrm{BCA}}+\widehat{\mathrm{CAB}}=180^{\circ}.
Puisque \widehat{\mathrm{BAC}}+\widehat{\mathrm{ABC}}=78^{\circ}+60^{\circ}=138^{\circ} alors \widehat{\mathrm{ACB}}=180^{\circ}-138^{\circ}=42^{\circ}.
Puisque \widehat{\mathrm{BAC}}+\widehat{\mathrm{ABC}}=78^{\circ}+60^{\circ}=138^{\circ} alors \widehat{\mathrm{ACB}}=180^{\circ}-138^{\circ}=42^{\circ}.


Définition
Le cercle circonscrit à un triangle est le cercle passant par les trois sommets du triangle.
Propriété
Le centre du cercle circonscrit à un triangle est le point de concours des trois médiatrices de ce triangle.

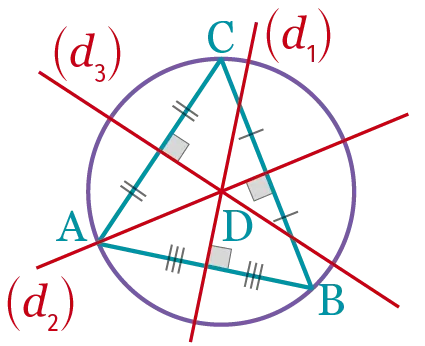
Version interactive
- Remarque : Le centre du cercle circonscrit peut se trouver à l'extérieur du triangle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Triangles rectangles
Définitions
Un triangle rectangle est un triangle possédant un angle droit.
Le côté opposé à l'angle droit s'appelle l'hypoténuse.
Propriété
Dans un triangle rectangle, l'hypoténuse est toujours le plus grand côté.
Propriété
La somme des deux angles aigus d'un triangle rectangle est égale à 90°.
Exemple :

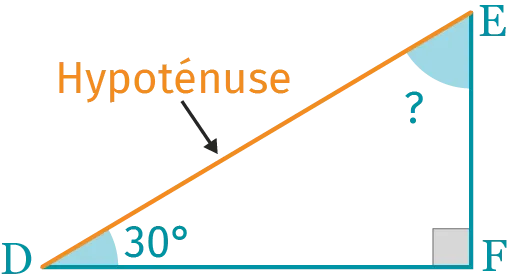
\mathrm{DEF} est un triangle rectangle en \mathrm{F}.
L'angle \widehat{\mathrm{DFE}} est un angle droit. L'hypoténuse est le segment [\mathrm{DE}]. On sait alors que : \widehat{\mathrm{FDE}}+\widehat{\mathrm{DEF}}=90^{\circ} c'est-à-dire 30^{\circ}+\widehat{\mathrm{DEF}}=90^{\circ}. Par conséquent, \widehat{\mathrm{DEF}}=90^{\circ}-30^{\circ}=60^{\circ}.
L'angle \widehat{\mathrm{DFE}} est un angle droit. L'hypoténuse est le segment [\mathrm{DE}]. On sait alors que : \widehat{\mathrm{FDE}}+\widehat{\mathrm{DEF}}=90^{\circ} c'est-à-dire 30^{\circ}+\widehat{\mathrm{DEF}}=90^{\circ}. Par conséquent, \widehat{\mathrm{DEF}}=90^{\circ}-30^{\circ}=60^{\circ}.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Triangles isocèles et équilatéraux
Définitions
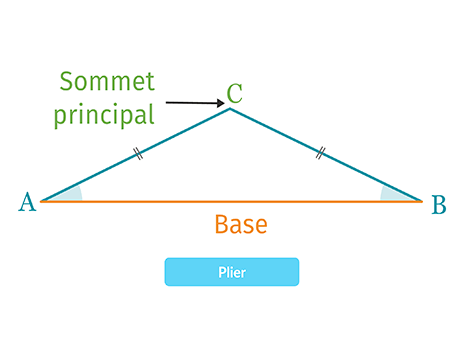
Un triangle isocèle est un triangle possédant deux côtés de même longueur. Le sommet commun aux deux côtés de même longueur s'appelle le sommet principal. Le côté opposé au sommet principal s'appelle la base.
Propriété
Dans un triangle isocèle, les angles à la base ont la même mesure.
Exemple :

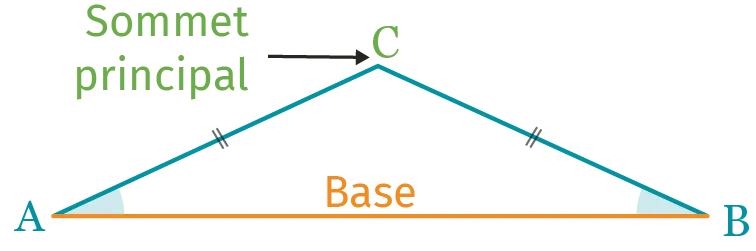
\mathrm{ABC} est isocèle en \mathrm{C} (le sommet principal), sa base est le côté [\mathrm{AB}].
Les angles \widehat{\mathrm{CAB}} et \widehat{\mathrm{ABC}} ont la même mesure.
Les angles \widehat{\mathrm{CAB}} et \widehat{\mathrm{ABC}} ont la même mesure.


- Remarque : Il est possible que l'angle situé au niveau du sommet principal d'un triangle isocèle soit un angle droit. Dans ce cas, on dit que c'est un triangle isocèle rectangle.
Définition
Un triangle équilatéral est un triangle possédant trois côtés de même longueur.
Propriété
Dans tout triangle équilatéral, chaque angle mesure 60°.

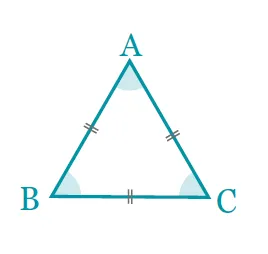
Démonstration :
Soit \mathrm{ABC} un triangle équilatéral. Démontrons que les angles ont la même mesure.
\mathrm{ABC} est isocèle en \mathrm{A} donc \widehat{\mathrm{ABC}}=\widehat{\mathrm{ACB}}. Il est aussi isocèle en \mathrm{B} donc \widehat{\mathrm{ACB}}=\widehat{\mathrm{CAB}}. Ainsi \widehat{\mathrm{ABC}}=\widehat{\mathrm{ACB}}=\widehat{\mathrm{CAB}}. Puisque la somme des angles est 180^{\circ} et que 180 \div 3=60, alors chacun des angles mesure 60^{\circ}.
Soit \mathrm{ABC} un triangle équilatéral. Démontrons que les angles ont la même mesure.
\mathrm{ABC} est isocèle en \mathrm{A} donc \widehat{\mathrm{ABC}}=\widehat{\mathrm{ACB}}. Il est aussi isocèle en \mathrm{B} donc \widehat{\mathrm{ACB}}=\widehat{\mathrm{CAB}}. Ainsi \widehat{\mathrm{ABC}}=\widehat{\mathrm{ACB}}=\widehat{\mathrm{CAB}}. Puisque la somme des angles est 180^{\circ} et que 180 \div 3=60, alors chacun des angles mesure 60^{\circ}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille