Préparer le brevet

64

D'après brevet, Métropole, juin 2014

Durée : 15 min

Un sac contient 20 jetons jaunes, verts, rouges ou bleus ayant chacun la même probabilité d'être tiré. On considère l'expérience : tirer au hasard un jeton, noter sa couleur et le remettre dans le sac.

1. Le professeur, qui connaît la composition du sac, a simulé un grand nombre de fois l'expérience avec un tableur. Il a représenté ci‑dessous la fréquence d'apparition des différentes couleurs après 1 000 tirages.



a. Quelle couleur est la plus présente ?

b. Le professeur a construit la feuille de calcul suivante.

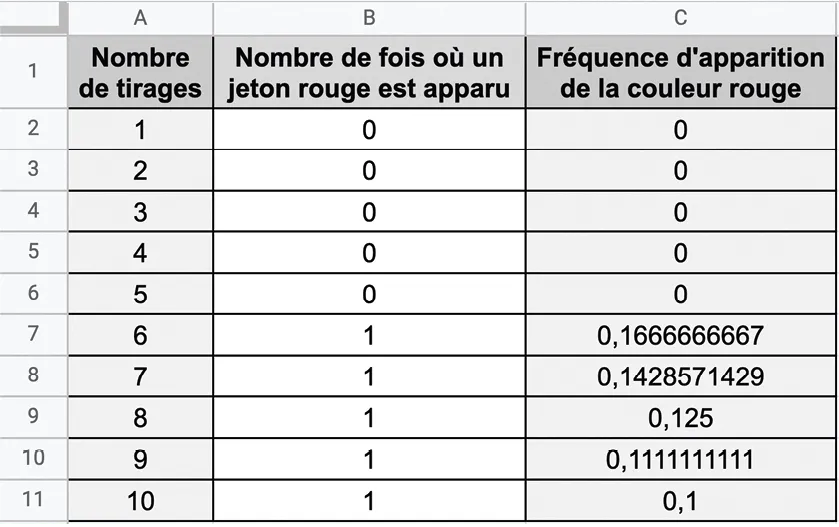
Quelle formule a‑t‑il saisie dans la cellule C2 avant de l'étirer vers le bas ?

2. On sait que la probabilité de tirer un jeton rouge est de \frac{1}{5}. Combien y a‑t‑il de jetons rouges dans ce sac ?

65

D'après brevet, Grèce, juin 2019

Durée : 15 min

Mathilde fait tourner deux roues de loterie A et B comportant chacune quatre secteurs numérotés comme sur le schéma ci‑dessous.

La probabilité d'obtenir chacun des secteurs d'une roue est la même. Les flèches rouges indiquent les deux secteurs obtenus. L'expérience de Mathilde est la suivante : elle fait tourner les deux roues pour obtenir un nombre à deux chiffres. Le chiffre obtenu avec la roue A est le chiffre des dizaines et celui avec la roue B est le chiffre des unités. Dans l'exemple ci‑contre, elle obtient le nombre 27 (roue A : 2 et roue B : 7).

1. Écrire tous les nombres possibles issus de cette expérience.

2. Prouver que la probabilité d'obtenir un nombre supérieur à 40 est 0{,}25.

3. Quelle est la probabilité que Mathilde obtienne un nombre divisible par 3 ?

66

D'après brevet, Amérique du Nord, 2019

Durée : 10 min

Expérience n°1 : Prendre au hasard un nombre entier compris entre 1 et 11 (inclus).
Expérience n°2 : Lancer un dé équilibré à six faces numérotées de 1 à 6 et annoncer le numéro qui apparaît sur la face du dessus.

Est‑il plus probable de prendre un nombre premier dans l'expérience 1 ou d'obtenir un nombre pair dans l'expérience 2 ?