Nos classiques
Sommaire
Mes pages
N° Page
Partie 1 : Nombres et calculs
Partie 2 : Organisation et gestion de données, fonctions
Partie 3 : Espace et géométrie
Partie 4 : Mesures et grandeurs
Annexes
Nos dossiers d'actualité
Dossier d'actualité
/ 303
Chapitre 12
Activités

Transformations dans le plan et leurs effets

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Activité 1
Une nouvelle transformation

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Objectif
Découvrir les rotations et leurs propriétés.
Cours 1 p. 232.

1
a) Quelles sont les trois transformations du plan connues ?
b) Quels sont leurs éléments caractéristiques ?
c) On considère la figure rose \text{F} suivante. L'une des quatre figures n'est pas l'image de \text{F} par l'une de ces trois transformations. Laquelle ?

5 figures géométriques identiques mais orientées de 5 façons différentes.
2
On considère maintenant la figure suivante.

Figure ABCD et figure A'B'C'D'.

a) Mesurer les longueurs \text{EA,} \text{EB,} \text{EA}^\prime et \text{EB}^\prime. Que remarquez-vous ?
b) Sans mesurer, conjecturer d'autres égalités avec les longueurs \text{EC} et \text{ED.}
c) Mesurer les angles \widehat{\mathrm{AEA}^{\prime}} et \widehat{\mathrm{BEB}^{\prime}}. Que remarquez‑vous ?
d) Sans mesurer, conjecturer d'autres égalités d'angles de sommet \text{E.}
On dit que le quadrilatère \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime} \mathrm{D}^{\prime} est l'image du quadrilatère \text{ABCD} par la rotation de centre \text{E} et d'angle 60° dans le sens horaire.

3
a) Mesurer les longueurs des côtés de ces deux quadrilatères. Que remarquez‑vous ?
b) Mesurer les angles des deux figures. Que remarquez‑vous ?
Bilan
Quels sont les effets d'une rotation sur les longueurs et les angles d'une figure ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Activité 2
Agrandir ou réduire

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Objectif
Déterminer les caractéristiques d'une homothétie.
Cours 2 p. 234.

On a construit avec GeoGebra la figure suivante. Les figures ne sont pas en vraies dimensions.
Triangle A'B'C' rectangle en A' et triangle ABC rectangle en A, puis un point D.

1
À l'aide des mesures des angles de la figure 1 que peut‑on dire des triangles \text{ABC} et \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime} ?
2
Que peut-on en déduire pour les longueurs des côtés homologues ?
3
Le logiciel donne les mesures suivantes.

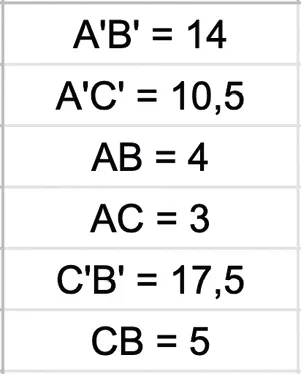
Placeholder pour Tableau schématique illustrant des mesures de longueurs : A'B'=14, A'C'=10,5, AB=4, AC=3, C'B'=17,5, CB=5.Tableau schématique illustrant des mesures de longueurs : A'B'=14, A'C'=10,5, AB=4, AC=3, C'B'=17,5, CB=5.

Quel est le coefficient d'agrandissement qui permet d'obtenir le triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime} à partir du triangle \text{ABC} ?
4
Le logiciel donne également les distances suivantes.

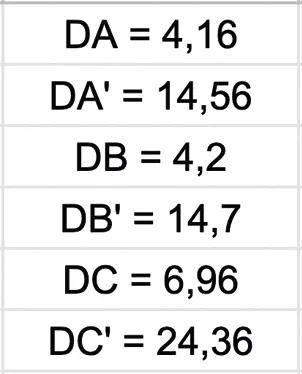
Placeholder pour Tableau de données numériques : valeurs DA, DA', DB, DB', DC, DC'Tableau de données numériques : valeurs DA, DA', DB, DB', DC, DC'

Comparer les distances de \text{D} aux sommets du triangle \text{ABC} avec celles de \text{D} aux sommets du triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime}. Que remarque‑t‑on ?

On dit que le triangle \mathrm{A}^{\prime} \mathrm{B}^{\prime} \mathrm{C}^{\prime} est l'image du triangle \text{ABC} par l'homothétie de centre \text{D} et de rapport 3{,}5.
5
On change uniquement le rapport de l'homothétie et on obtient la figure 2 ci‑dessous.

Triangle A'B'C' rectangle en A' et triangle ABC rectangle en A, puis un point D.

Les longueurs restent inchangées. Quel pourrait être le rapport de cette homothétie ?
6
Quelle est la différence avec l'homothétie de la figure 1 ? Proposer un moyen pour différencier ces deux cas.
Bilan
De quels éléments a‑t‑on besoin pour construire l'image d'une figure par une homothétie ?
Afficher la correction
Fermer
Page précédente
Page suivante

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.