Chapitre 6
TP / TICE 1
Étudier le lieu géométrique d'un point du plan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Question préliminaire
Que peut-on dire de l'abscisse et de l'ordonnée de \text{B}
lorsque le point se déplace sur la droite d ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Déterminer, à l'aide d'une des trois méthodes, l'ensemble
parcouru par le point \text{D} lorsque \text{B} parcourt la droite d .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
1. Préparer une feuille de calcul dans laquelle on
trouvera deux colonnes pour les coordonnées de
\text{B} et deux colonnes pour les coordonnées de \text{D} . La
colonne de l'ordonnée de \text{B} sera complétée uniquement
avec des 5.

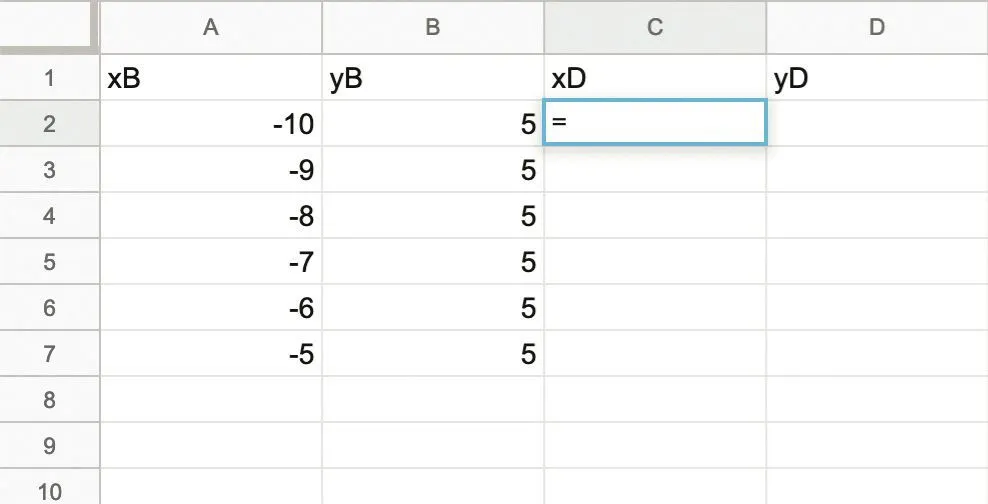
2. Exprimer les coordonnées du point \text{D} en fonction de celles du point \text{B} .


2. Exprimer les coordonnées du point \text{D} en fonction de celles du point \text{B} .
3. a. Compléter la colonne de l'abscisse de \text{B} avec
tous les entiers de -10 à 10.
b. Compléter alors les colonnes des coordonnées de \text{D} en utilisant les bonnes formules. Que remarque-t-on ?
4. a. Dans un graphique, construire le nuage de points correspondant aux deux colonnes des coordonnées de \text{D} .
b. Quel est le lieu géométrique du point \text{D} ?
b. Compléter alors les colonnes des coordonnées de \text{D} en utilisant les bonnes formules. Que remarque-t-on ?
4. a. Dans un graphique, construire le nuage de points correspondant aux deux colonnes des coordonnées de \text{D} .
b. Quel est le lieu géométrique du point \text{D} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Geogebra
1. Construire la figure.
Pour le point \text{D} , on utilisera la saisie suivante.




2. En activant la trace de \text{D} , déterminer son lieu géométrique lorsque \text{B} se déplace sur la droite d .
3. On rappelle que \overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}.
a. Déterminer la relation existant entre \overrightarrow{\text{AC}} et \overrightarrow{\text{BD}}.
b. En déduire que les coordonnées du vecteur \overrightarrow{\text{BD}} sont constantes.
c. Déterminer alors l'ordonnée du point \text{D} .
4. Comment expliquer la trace de \text{D} sur GeoGebra ?
3. On rappelle que \overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}.
a. Déterminer la relation existant entre \overrightarrow{\text{AC}} et \overrightarrow{\text{BD}}.
b. En déduire que les coordonnées du vecteur \overrightarrow{\text{BD}} sont constantes.
c. Déterminer alors l'ordonnée du point \text{D} .
4. Comment expliquer la trace de \text{D} sur GeoGebra ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 3Python
1. Quelles instructions permettent de connaître les
coordonnées de \text{D} en fonction de celles de \text{A} , \text{B}
et \text{C}.
2. Écrire un programme Python utilisant une boucle portant sur l'abscisse de \text{B} qui permet de calculer et d'afficher les coordonnées de \text{D} à chaque itération.
2. Écrire un programme Python utilisant une boucle portant sur l'abscisse de \text{B} qui permet de calculer et d'afficher les coordonnées de \text{D} à chaque itération.
3. Exécuter le programme.
4. Conjecturer le lieu géométrique de \text{D} lorsque \text{B} se déplace sur d .
4. Conjecturer le lieu géométrique de \text{D} lorsque \text{B} se déplace sur d .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Écrire un programme Python qui permette de
représenter graphiquement le lieu géométrique
de \text{D} lorsque \text{B} se déplace sur d .
On pourra par exemple utiliser la librairie \bf{turtle}.
On pourra par exemple utiliser la librairie \bf{turtle}.
Fermer
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
