Mathématiques 1re Spécialité
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Exercices flash
Chapitre 5
Entraînement
Exercices FLASH
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Étudier les variations de chacune des fonctions
suivantes.
1. f est la fonction définie sur \R par f(x) = -3x + 2 et dérivable sur \R .
2. g est la fonction définie sur \R^* par g ( x ) = \dfrac { - 2 } { x } et dérivable sur \R^*.
3. h est la fonction définie sur \R par h(x) = x^3 + x et dérivable sur \R.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
f est une fonction définie et dérivable sur son ensemble de définition. On donne ci-dessous le tableau de variations de f .
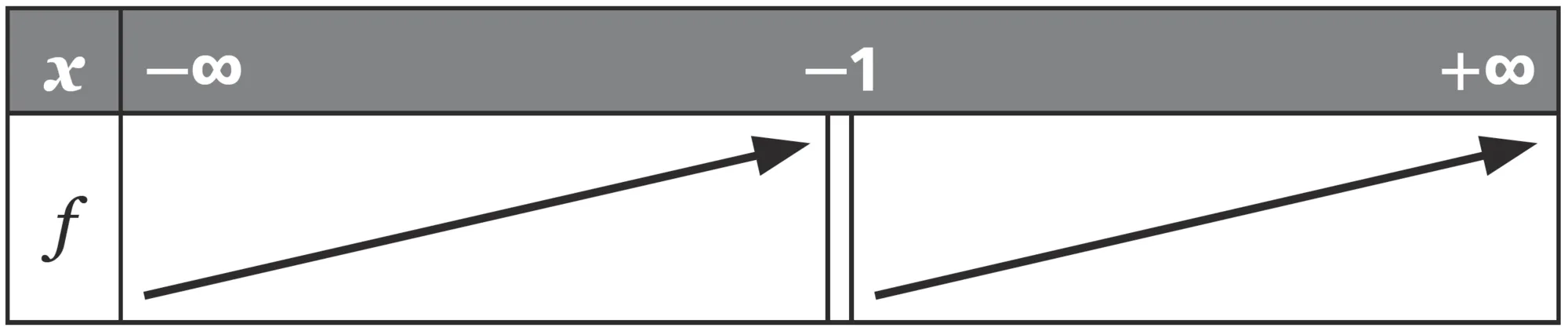
2. Comparer si possible :
a. f(-3) et f(-2) \: ;
b. f(-3) et f(2) .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
g est une fonction définie sur \R .
g ^ { \prime } est la fonction dérivée de g définie sur \R par g ^ { \prime } ( x ) = \dfrac { - 2 } { x ^ { 2 } + 9 }. 1. Comparer g(3) et g(-7).
2. Comparer -g(4) et -g(10).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
On donne ci-après le tableau de variations
d'une fonction h définie et dérivable sur \R .
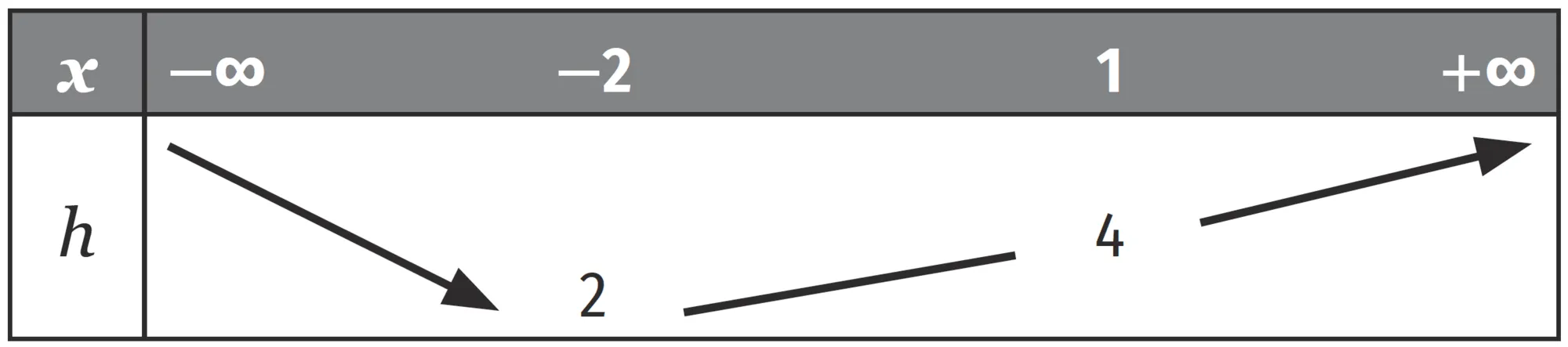
2. Quel est le signe de h sur \R \:?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
On donne ci-dessous la courbe représentative
d'une fonction k définie et dérivable sur [-4\: ; 4].
1. Quel est le signe de :
a. k ^ { \prime } ( 3 ) \:?
b. k ^ { \prime } ( 0 ) \:?
c. k ^ { \prime } ( -3 ) \:?
a. k ^ { \prime } ( 3 ) \:?
b. k ^ { \prime } ( 0 ) \:?
c. k ^ { \prime } ( -3 ) \:?
2. Comparer :
a. k ^ { \prime } ( 2\text{,}5 ) et k ^ { \prime } ( 3 ) \:;
b. k ^ { \prime } ( -1\text{,}5 ) et k ^ { \prime } ( 3-1\text{,}25 ) \:;
c. k ^ { \prime } ( -1\text{,}5 ) et k ^ { \prime } ( 3 ).
a. k ^ { \prime } ( 2\text{,}5 ) et k ^ { \prime } ( 3 ) \:;
b. k ^ { \prime } ( -1\text{,}5 ) et k ^ { \prime } ( 3-1\text{,}25 ) \:;
c. k ^ { \prime } ( -1\text{,}5 ) et k ^ { \prime } ( 3 ).
Fermer
p. 144
100%
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
