Chapitre 9
Synthèse
Exercices de synthèse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
99
[Représenter, Raisonner.]
Soit f la fonction définie sur \R par :
f(x)=2 \cos \left(\frac{3 x}{\pi}\right)-3 \sin ^{2}\left(\frac{4 x}{\pi}\right)+1.
1. Uniquement à l'aide de la calculatrice et sans justifier :
a. préciser si f(0) = -2 ;
b. préciser si f\left(\frac{\pi^{2}}{6}\right)=\frac{-5}{4} ;
c. préciser si f est paire ou impaire ;
d. préciser si f est périodique de période 2\pi ;
e. déterminer le nombre de solutions sur [-2\pi~; 2\pi] de l'équation f(x) = 0 ;
a. préciser si f(0) = -2 ;
b. préciser si f\left(\frac{\pi^{2}}{6}\right)=\frac{-5}{4} ;
c. préciser si f est paire ou impaire ;
d. préciser si f est périodique de période 2\pi ;
e. déterminer le nombre de solutions sur [-2\pi~; 2\pi] de l'équation f(x) = 0 ;
f. déterminer la limite éventuelle de f(x) en +\infty ;
g. préciser si f'(0)=0 ;
h. préciser si f'\left(\frac{\pi^{2}}{6}\right)=\frac{-12}{\pi}.
2. Préciser si sa dérivée f' est définie sur \R par f^{\prime}(x)=\frac{-6}{\pi} \sin \left(\frac{3 x}{\pi}\right)-\frac{12}{\pi} \sin \left(\frac{8 x}{\pi}\right).
g. préciser si f'(0)=0 ;
h. préciser si f'\left(\frac{\pi^{2}}{6}\right)=\frac{-12}{\pi}.
2. Préciser si sa dérivée f' est définie sur \R par f^{\prime}(x)=\frac{-6}{\pi} \sin \left(\frac{3 x}{\pi}\right)-\frac{12}{\pi} \sin \left(\frac{8 x}{\pi}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
100
[Calculer, Chercher.]
Soit f la fonction définie sur \R par f(x)=2 \cos (2 x)-1.
1. Résoudre dans \R l'équation f(x) = 0.
2. Déterminer la plus petite période \text{T} de f.
3. Montrer qu'il est possible de restreindre l'étude de f à \left[0~; \frac{\pi}{2}\right].
4. Démontrer que sur \left[0~; \frac{\pi}{2}\right], f^{\prime}(x) \leqslant 0.
2. Déterminer la plus petite période \text{T} de f.
3. Montrer qu'il est possible de restreindre l'étude de f à \left[0~; \frac{\pi}{2}\right].
4. Démontrer que sur \left[0~; \frac{\pi}{2}\right], f^{\prime}(x) \leqslant 0.
5. Construire le tableau de variations de f sur [-\pi~; \pi].
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
101
Devoir maison
[Chercher, Raisonner.]
Partie A
La courbe suivante représente sur [-\pi~; \pi] la fonction f définie par f(x)=a x+b \cos (x)+c.
Déterminer les réels a, b et c, sachant que la tangente à la courbe au point \text{A} d'abscisse \frac{-\pi}{2} est horizontale et que celle au point \text{B} de coordonnées (0~; 3) a pour coefficient directeur -2.
Partie B
Soit g la fonction définie sur \R par :
g(x)=-2 x+2 \cos (x)+1.
1. Montrer que la fonction g est strictement décroissante sur \R.
2. Montrer que sur \left[0~; \frac{\pi}{2}\right], l'équation g(x)=0 admet une unique solution \alpha et encadrer \alpha au dixième.
3. En déduire le signe de g(x) sur \R.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
102
[Représenter, Chercher.]
À tout réel x de \left] 0\,; \frac{\pi}{2}\right[, on fait correspondre le point \mathrm{M}(x) du cercle trigonométrique. La perpendiculaire à (\mathrm{OM}(x)) passant par \mathrm{M}(x) coupe alors respectivement les axes des abscisses et des ordonnées aux points \mathrm{A}(x) et \mathrm{B}(x). Dans la suite, g(x) désigne l'aire du triangle \mathrm{OA}(x) \mathrm{B}(x).
1. Faire une figure complète pour x=\frac{\pi}{6}.
2. Déterminer les coordonnées du point \mathrm{A}(x) en fonction de x.
3. En admettant que \mathrm{OB}(x)=\frac{1}{\sin (x)}, montrer que g(x)=\frac{1}{\sin (2 x)}.
4. Déterminer x pour que g(x) soit minimale et déterminer cette aire.
Aide
On pourra utiliser le produit scalaire.
3. En admettant que \mathrm{OB}(x)=\frac{1}{\sin (x)}, montrer que g(x)=\frac{1}{\sin (2 x)}.
4. Déterminer x pour que g(x) soit minimale et déterminer cette aire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
103
[Modéliser, Calculer.]
Un jardinier souhaite apposer à sa maison un abri pour ses outils. Il en a déjà dessiné un plan qui a la forme d'un trapèze isocèle comme l'illustre la figure ci‑après.

Il cherche l'angle \theta qui permettrait de maximiser la surface au sol à l'aide du calcul formel. 1. Montrer que l'aire de la figure peut s'exprimer par une fonction f définie sur \left] 0~; \frac{\pi}{2}\right[ par f(x)=4 \cos (x)(1+\sin (x)) où x est une mesure de l'angle \theta étudié.
2. Montrer que f est dérivable sur son intervalle de définition et que, pour tout x \in\left] 0~; \frac{\pi}{2}\right[, on a f^{\prime}(x)=-8 \sin ^{2}(x)-4 \sin (x)+4.
3. Un logiciel de calcul formel donne le résultat suivant :

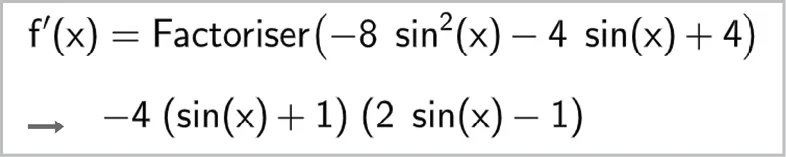
En déduire le tableau de variations de f sur \left] 0~; \frac{\pi}{2}\right[.
Cliquez pour accéder à une zone de dessin
4. Conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
104
Approfondissement
[Calculer, Raisonner.]
La fonction tangente est la fonction f définie pour tout réel x tel que \cos (x) \neq 0 par :
f(x)=\tan (x)=\frac{\sin (x)}{\cos (x)}.
1. Pour quelles valeurs de x de l'intervalle [-2 \pi~; 2 \pi] la fonction f n'est‑elle pas définie ?
Compléter le tableau de valeurs suivant.
2. Déterminer la limite de \tan (x) lorsque x tend vers \frac{\pi}{2} en lui étant inférieur.
3. Montrer que f est à la fois impaire et périodique de période \pi.
4. Justifier que l'on peut réduire l'étude de f à l'intervalle \left[0~; \frac{\pi}{2}\right[.
Compléter le tableau de valeurs suivant.
| \boldsymbol{\textcolor{#ffffff}{a}} | 0 | \frac{\pi}{6} | \frac{\pi}{4} | \frac{\pi}{3} | \frac{5\pi}{6} |
| \boldsymbol{\textcolor{#ffffff}{\tan a}} |
2. Déterminer la limite de \tan (x) lorsque x tend vers \frac{\pi}{2} en lui étant inférieur.
3. Montrer que f est à la fois impaire et périodique de période \pi.
4. Justifier que l'on peut réduire l'étude de f à l'intervalle \left[0~; \frac{\pi}{2}\right[.
5. Montrer que f est dérivable sur \left[0~; \frac{\pi}{2}\right[ et que sa fonction dérivée f' est définie, pour tout x \in\left[0~; \frac{\pi}{2}\right[, par f^{\prime}(x)=\frac{1}{\cos ^{2}(x)}.
6. Déterminer les variations de f sur \left[0~; \frac{\pi}{2}\right[.
7. Construire le tableau de variations de f sur [-\pi~; \pi] \cap \mathcal{D}_{f} où \mathcal{D}_{f} est l'ensemble de définition de f.
6. Déterminer les variations de f sur \left[0~; \frac{\pi}{2}\right[.
7. Construire le tableau de variations de f sur [-\pi~; \pi] \cap \mathcal{D}_{f} où \mathcal{D}_{f} est l'ensemble de définition de f.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
105
Maths expertes
[Chercher, Communiquer.]
Soient a et b deux entiers naturels non nuls.
Quelle est la plus petite période de la fonction f définie sur \R par f(x)=\cos (a x)+\sin (b x) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le Grand Oral
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Choisir une problématique
Exemple de sujet : Les équations différentielles
du deuxième ordre
Méthode
❯ Une fois que vous avez choisi () et cadré () votre sujet, vous devez le formuler sous la forme d'une question que vous allez essayer de résoudre.❯ La façon dont vous allez formuler votre sujet va indiquer l'angle sous lequel vous avez choisi de le traiter.
❯ Qu'est‑ce qu'une bonne problématique ?
- une question à laquelle on ne peut répondre par oui ou par non, la réponse n'est pas évidente ;
- une question qui n'est ni trop large ni trop précise : l'angle choisi doit vous permettre de traiter les principaux aspects du sujet ;
- une question qui fait éventuellement écho à des préoccupations actuelles.
❯ Votre problématique peut être amenée à évoluer au fil de vos recherches, c'est normal !
Exemples de problématiques sur ce sujet
❯ Comment résoudre une équation différentielle du deuxième ordre ?Cette problématique est trop vague, il sera difficile de répondre à cette question en 5 minutes.
❯ Comment résoudre l'équation différentielle \boldsymbol{y''= -2y} ?
Cette problématique est trop précise. À part présenter la solution, il n'y a pas beaucoup d'autres enjeux.
❯ Comment les fonctions trigonométriques permettentelles de construire les solutions d'une équation différentielle du deuxième ordre ?
Ceci pourrait constituer une problématique intéressante car elle permet d'aborder les dérivées des fonctions trigonométriques ainsi que la construction d'une solution. D'autres problématiques sont évidemment possibles.
Fermer
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

