Physique-Chimie 4e
Nouveau manuel de Sciences et Technologie 6e
Découvrez cet ouvrage collaboratif, conforme au nouveau programme !
Mes Pages
Thème 1 : Organisation et transformations de la matière
Ch. 1
La matière, dans l'espace et dans l'Univers
Ch. 2
Que trouve-t-on dans l'air ?
Ch. 3
Les transformations chimiques et la pollution
Ch. 4
Modélisation des transformations chimiques
Ch. 5
Introduction à la masse volumique
Thème 2 : Mouvement et interactions
Ch. 6
Repérage de mouvement et mesure de vitesse
Ch. 7
Les interactions
Thème 3 : L'énergie et ses conversions
Ch. 8
Conversion et transfert de l'énergie
Ch. 9
La tension et l'intensité
Ch. 10
Relations entre grandeurs dans les circuits électriques
Thème 4 : Des signaux pour observer et communiquer
Ch. 11
Vitesse de propagation des signaux
Chapitre 5
Accompagnement personnalisé
Manipuler des outils thématiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je sais faire si
- J'utilise les mathématiques comme un outil pour modéliser un phénomène physique.
- Les mathématiques me permettent d'écrire des lois.
- Les mathématiques me permettent de prévoir des comportements et, parfois, de découvrir de nouveaux phénomènes.
- Je les maitrise pour appréhender certaines théories scientifiques.
- Je les mets en application pour répondre à une question concernant un problème connu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Un exercice pour s'entrainer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Vérification de la nature d'un matériau
Pour vérifier la nature d'un échantillon de matière solide, il faut connaitre la masse volumique de la substance supposée de l'échantillon et aussi pouvoir mesurer sa masse et son volume. La mesure de la masse est assez simple car on trouve facilement des balances. Si la forme n'est pas une figure géométrique connue, le volume est alors plus compliqué à déterminer. On peut dans certaines circonstances (si l'objet n'est pas trop gros) utiliser le déplacement de l'eau.
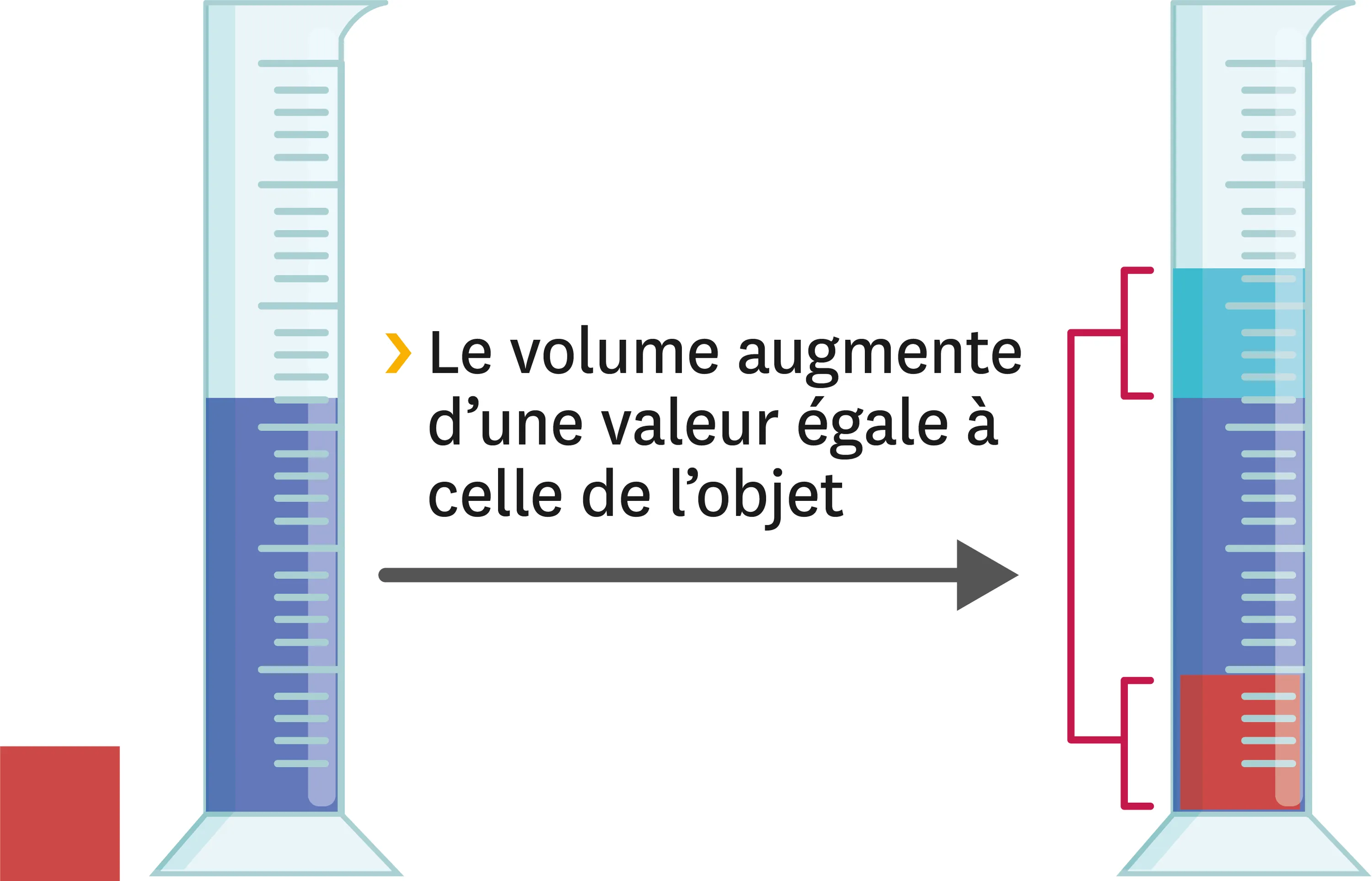
Considérons par exemple un pavé droit de zinc de 2 cm de large, 2 cm de haut et 2,5 cm de long. La masse volumique du zinc est de 7,1 g/cm3.
Considérons par exemple un pavé droit de zinc de 2 cm de large, 2 cm de haut et 2,5 cm de long. La masse volumique du zinc est de 7,1 g/cm3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Si tu n'as pas d'éprouvette assez grosse pour y faire entrer l'échantillon, tu peux utiliser la méthode du débordement. Attention : il faut bien récupérer toute l'eau qui déborde et bien mesurer son volume.
2. Si tu préfères le calcul, le volume d'un pavé droit est égal au produit de ses trois arrêtes (a × b × c). La masse m que devrait avoir l'échantillon est égale au produit du volume V par la masse volumique ρ du zinc. C'est-à-dire m = ρ × V pour le calcul, il faut faire attention aux unités !
3. Pour vérifier que la masse réelle correspond bien à la masse théorique d'un cube en zinc, utilise une balance précise.
2. Si tu préfères le calcul, le volume d'un pavé droit est égal au produit de ses trois arrêtes (a × b × c). La masse m que devrait avoir l'échantillon est égale au produit du volume V par la masse volumique ρ du zinc. C'est-à-dire m = ρ × V pour le calcul, il faut faire attention aux unités !
3. Pour vérifier que la masse réelle correspond bien à la masse théorique d'un cube en zinc, utilise une balance précise.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Question
1. Quelle doit-être la masse de notre cube s'il est réellement en zinc ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice similaire
1. Un cube de cuivre de 2 cm d'arrête a été coupé en deux selon sa diagonale. Calcule la masse en g des deux morceaux de cubes obtenus sachant que ρcuivre = 8,920 g/cm3.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
