Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Thème 1 - Organisation et transformations de la matière
Ch. 1
L'eau que nous buvons est-elle pure ?
Ch. 2
La matière : états, masse et volume
Ch. 3
Les changements d'état de la matière
Ch. 4
Les mélanges
Ch. 5
La matière à l'échelle microscopique
Ch. 6
Que trouve-t-on dans l'air ?
Ch. 7
Les transformations chimiques et la pollution
Ch. 8
Modélisation des transformations chimiques
Ch. 9
Les ions dans notre quotidien
Ch. 10
Quand les acides et les bases réagissent
Ch. 11
Introduction à la masse volumique
Ch. 12
La masse volumique
Ch. 13
La matière, dans l'espace et dans l'Univers
Ch. 14
De l'Univers aux atomes
Thème 2 - Mouvement et interactions
Ch. 15
Introduction à la vitesse et au mouvement
Ch. 16
Repérage de mouvement et mesure de vitesse
Ch. 17
Vitesse et mouvement
Ch. 18
Les interactions
Ch. 19
Les forces
Ch. 20
Le poids
Thème 3 - L'énergie et ses conversions
Ch. 21
Introduire la notion d'énergie
Ch. 22
Conversion et transfert de l'énergie
Ch. 23
La conservation de l'énergie
Ch. 24
Les circuits électriques
Ch. 25
La tension et l'intensité
Ch. 26
Relations entre grandeurs dans les circuits électriques
Ch. 27
Résistance et loi d'Ohm
Ch. 28
Puissance et énergie en électricité
Thème 4 - Des signaux pour observer et communiquer
Ch. 29
Le son
Ch. 30
La lumière
Ch. 31
Vitesse de propagation des signaux
Ch. 32
Des signaux au-delà de la perception humaine
Chapitre 1
Exercices
18 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je me teste
Je sais
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Quelle valeur correspond à la distance Terre-Lune ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Choisis le bon classement, du plus grand au plus petit.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Planète ou étoile ?
Glisse ces corps célestes dans la bonne colonne du tableau en fonction de leur catégorie :
| Planète | Étoile |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Complète la grille de mots-croisés.
Vertical :
1. Satellite naturel de la Terre.
2. Troisième planète du système solaire.
3. La nôtre s'appelle la Voie lactée.
4. Étoile la plus proche de la Terre.
1. Satellite naturel de la Terre.
2. Troisième planète du système solaire.
3. La nôtre s'appelle la Voie lactée.
4. Étoile la plus proche de la Terre.
Horizontal :
5. Ont été déposés sur la Lune lors de missions spatiales.
6. Il n'y a pas plus grand que lui.
7. Le Soleil en est un exemple.
5. Ont été déposés sur la Lune lors de missions spatiales.
6. Il n'y a pas plus grand que lui.
7. Le Soleil en est un exemple.
Cette fonctionnalité est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je sais faire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Pour calculer la distance Terre-Lune, connaissant la valeur de la durée d'un aller-retour effectué par la lumière entre la Terre et la Lune :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Une histoire de distances.
Parmi ces unités, cherche l'intrus :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Quelle est la bonne conversion ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Parmi ces propositions, quel est l'équivalent de 1,5 \times 10^8 km ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9Par seconde, la lumière parcourt :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice corrigé
Compétence : Présenter mon résultat avec l'unité adaptée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10Distance Soleil-Sirius.
Parmi toutes les étoiles visibles la nuit depuis la Terre, Sirius se situe à 8,2 × 1013 km du Soleil.
1. Convertis cette distance en unités astronomiques.
2. Convertis cette distance en années-lumière.
1 UA = 1,5 × 108 km et 1 a.l. = 9,5 × 1012 km
1. Convertis cette distance en unités astronomiques.
1 UA = 1,5 × 108 km et 1 a.l. = 9,5 × 1012 km
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étapes de la méthode
- Rappeler la relation de conversion entre les deux unités.
Par exemple : 1 \: \text{unité} 1 = a \times \text{unité} 2. - Reformuler éventuellement la relation de conversion pour que l'unité de départ soit égale à un nombre ou un quotient multiplié par l'unité d'arrivée.
Par exemple : 1 \: \text{unité} 2 = \dfrac{1}{a} \text{unité} 1. - Remplacer le symbole de l'unité de départ par une multiplication avec le deuxième membre de l'égalité précédente.
Par exemple : 1234 \: \text{unité} 2 = 1234 \times \dfrac{\text{unité} 1}{a}. - Effectuer l'opération puis écrire le résultat correspondant.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Corrigé
1. Je calcule la distance Soleil-étoile d en unités astronomiques.
Sachant que 1 UA = 1,5 x 108 km, j'en déduis que 1 km = \dfrac{1}{1\text{,}5 \times 10^{8}} UA.
Donc d = 8\text{,}2 \times 10^{13} km devient d =8\text{,}2 \times 10^{13} \times \dfrac{1}{1\text{,}5 \times10^8} UA
ce qui donne d = 5\text{,}5 \times 10^5 UA.
2. Je calcule la distance d Soleil-étoile en annés-lumière.
Puisque 1 a.l. = 9\text{,}5 \times 10^{12} km, j'en déduis que 1 km = \dfrac{1}{9\text{,}5 \times 10^{12}} a.l.
Donc d = 8\text{,}2 \times 10^{12} km devient d = 8\text{,}2 \times 10^{13} \times \dfrac{1}{9\text{,}5 \times 10^{12}} a.l.
ce qui donne d = 8\text{,}6 a.l.
Sachant que 1 UA = 1,5 x 108 km, j'en déduis que 1 km = \dfrac{1}{1\text{,}5 \times 10^{8}} UA.
Donc d = 8\text{,}2 \times 10^{13} km devient d =8\text{,}2 \times 10^{13} \times \dfrac{1}{1\text{,}5 \times10^8} UA
ce qui donne d = 5\text{,}5 \times 10^5 UA.
2. Je calcule la distance d Soleil-étoile en annés-lumière.
Puisque 1 a.l. = 9\text{,}5 \times 10^{12} km, j'en déduis que 1 km = \dfrac{1}{9\text{,}5 \times 10^{12}} a.l.
Donc d = 8\text{,}2 \times 10^{12} km devient d = 8\text{,}2 \times 10^{13} \times \dfrac{1}{9\text{,}5 \times 10^{12}} a.l.
ce qui donne d = 8\text{,}6 a.l.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice similaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11Distance Soleil-Canopus
Parmi toutes les étoiles visibles depuis la Terre la nuit, Canopus se situe à 1,15 \times 1016 km du Soleil.
1. Convertis cette distance en unités astronomiques.
2. Convertis cette distance en années-lumière.
1. Convertis cette distance en unités astronomiques.
2. Convertis cette distance en années-lumière.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je m'entraine
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12Quelques définitions.
Donne la définition des mots suivants.
1. Unité astronomique.
2. Année-lumière.
3. Galaxie.
2. Année-lumière.
3. Galaxie.
4. Planète géante.
5. Soleil.
6. Voie lactée.
5. Soleil.
6. Voie lactée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13Savoir utiliser une relation de conversion.
Une unité astronomique correspond à 150 000 000 de kilomètres.
Exprime les distances suivantes en unité astronomique (UA) en détaillant ton calcul.
1. 108,2 \times 10^6 km.
2. 382,9 \times 10^6 km.
3. 1 427,0 \times 10^6 km.
Exprime les distances suivantes en unité astronomique (UA) en détaillant ton calcul.
1. 108,2 \times 10^6 km.
2. 382,9 \times 10^6 km.
3. 1 427,0 \times 10^6 km.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14Le système solaire.
1. Qu'appelle-t-on le « système solaire » ?
2. Les planètes les plus petites sont des planètes telluriques. Quelle autre catégorie de planètes existe-t-il ?
3. Quelles sont les planètes les plus proches du Soleil ?
4. Quelles sont les planètes les plus éloignées du Soleil ?
2. Les planètes les plus petites sont des planètes telluriques. Quelle autre catégorie de planètes existe-t-il ?
3. Quelles sont les planètes les plus proches du Soleil ?
4. Quelles sont les planètes les plus éloignées du Soleil ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15Savoir utiliser des échelles.
1. Prends comme échelle 4 a.l. = 1 mm et représente les distances entre le Soleil et chacune de ces étoiles.
| Nom de l'étoile | Distance séparant le Soleil de la planète ou de l'étoile en a.l. |
| Altaïr | 16,5 |
| Canopus | 98 |
| Acrux | 120 |
| Spica | 220 |
| Mimosa | 490 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16Faire des conversions.
Complète les conversions suivantes et utilise la notation scientifique quand elle est utile :
1. 1 UA = km
2. 10 UA = km
3. 47,3 a.l. = km
4. 1,5 × 1012 km = UA
5. 1 a.l. = km
6. 20 a.l. = km
1. 1 UA =
2. 10 UA =
3. 47,3 a.l. =
4. 1,5 × 1012 km =
5. 1 a.l. =
6. 20 a.l. =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17Calcul de distance.
Compétence
Pratiquer le calcul numérique et le calcul littéral.
Le GPS utilise une constellation d'une vingtaine de satellites situés à une altitude de 20 184 km. Une telle répartition est essentielle pour qu'au moins six satellites repèrent de façon précise l'emplacement du récepteur GPS situé sur Terre.
Chaque satellite émet des signaux de façon régulière qui sont en quelque sorte sa carte d'identité.
1. Combien vaut environ la distance sol-satellite ?
2. Sachant que la lumière se propage à une vitesse d'environ 300 000 km/s, déduis-en la durée de propagation d'un signal émis entre le satellite et le récepteur GPS.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18Calculs de durées.
Depuis la Terre, tout ce qui concerne le Soleil est vu avec un certain décalage temporel. Quelle est la valeur de ce retard ?
1. Rappelle la valeur de la vitesse de propagation de la lumière dans le vide.
2. Sachant que la distance Terre-Soleil vaut approximativement 150 millions de km, calcule la durée de propagation puis exprime-la dans l'unité la plus adaptée.
3. Si une éclipse est annoncée pour 11 h 59, heure terrestre, à quelle heure le Soleil, la Terre et la Lune sont-ils réellement alignés ?
1. Rappelle la valeur de la vitesse de propagation de la lumière dans le vide.
2. Sachant que la distance Terre-Soleil vaut approximativement 150 millions de km, calcule la durée de propagation puis exprime-la dans l'unité la plus adaptée.
3. Si une éclipse est annoncée pour 11 h 59, heure terrestre, à quelle heure le Soleil, la Terre et la Lune sont-ils réellement alignés ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19Grandeur et unité.
1. Quelle relation mathématique existe-t-il entre les grandeurs suivantes : vitesse ; distance parcourue ; durée du parcours ?
2. Quelles sont les unités de ces trois grandeurs dans le système international ?
3. Cite une application utile de cette formule.
2. Quelles sont les unités de ces trois grandeurs dans le système international ?
3. Cite une application utile de cette formule.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20Des mots pour une phrase.
Utilise ces mots pour construire des phrases correctes.
1. Lune - Terre - satellite - unique - orbite - naturel.
2. Missions - Lune - distance - Terre - mesures - améliorer la précision.
3. Galaxie - Univers - système solaire - Voie lactée.
1. Lune - Terre - satellite - unique - orbite - naturel.
2. Missions - Lune - distance - Terre - mesures - améliorer la précision.
3. Galaxie - Univers - système solaire - Voie lactée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21Formation de l'Univers et du système solaire.
1. Les grandes structures de l'Univers sont-elles fixes ou en mouvement les unes par rapport aux autres ?
2. Comment s'appelle ce phénomène ?
2. Comment s'appelle ce phénomène ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22Différents types de planètes.
Écris une phrase contenant les mots ci-dessous.
1. Planète - Jupiter - Terre - planète géante.
2. Saturne - Terre - petite - grande.
3. Soleil - système solaire - planète - galaxie.
1. Planète - Jupiter - Terre - planète géante.
2. Saturne - Terre - petite - grande.
3. Soleil - système solaire - planète - galaxie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23Faire des schémas.
Compétence
Produire et transformer des tableaux ou des documents graphiques.
1. Avec des cercles et sans te soucier de l'échelle, représente les orbites des planètes autour du Soleil. Place les noms en légende.
2. Précise sur ce schéma où se trouvent les planètes telluriques et les géantes gazeuses.
3. Grâce à une double flèche partant du Soleil, précise à quelle distance correspond une unité astronomique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une notion, trois exercices Différenciation
Compétence : Concevoir une expérience pour tester une hypothèse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24-ADistances et durées dans le système solaire. Mesurer la distance Terre-Lune.
On peut mesurer la distance entre la Terre et la Lune à l'aide d'un laser tiré depuis la Terre : la lumière se réfléchit sur un réflecteur placé sur la Lune. Au moment de la mesure, les scientifiques ont trouvé que la distance entre la Terre et la Lune était de 3,90 \times 10^5 km. On va chercher à déterminer la durée qu'il faut à la lumière du laser pour parcourir cette distance.
1. Quelle relation mathématique permet de calculer une durée en connaissant une distance et une vitesse ?
2. Quelle est la valeur de la vitesse de la lumière dans le vide en km/s exprimée avec des puissances de 10 ?
3. Remplace dans la formule les symboles des grandeurs par leur valeur.
4. Effectue le calcul et exprime ton résultat en secondes.
1. Quelle relation mathématique permet de calculer une durée en connaissant une distance et une vitesse ?
2. Quelle est la valeur de la vitesse de la lumière dans le vide en km/s exprimée avec des puissances de 10 ?
3. Remplace dans la formule les symboles des grandeurs par leur valeur.
4. Effectue le calcul et exprime ton résultat en secondes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24-BDistances et durées dans le système solaire. Communiquer avec Mars.
Dans l'éventualité où l'homme arriverait à installer une station habitée sur Mars, un des problèmes qui se poserait serait celui de la communication avec la Terre. On utiliserait des signaux électromagnétiques qui se propageraient à la vitesse de la lumière. On cherche à savoir quelle durée prendraient ces signaux pour atteindre la Terre.
Donnée : distance Terre-Mars = 2,28 \times 108 km.
1. Quelle relation mathématique permet de calculer une durée en connaissant une distance et une vitesse ?
2. Applique cette formule et donne la durée mise par un signal pour parcourir la distance Terre-Mars.
Donnée : distance Terre-Mars = 2,28 \times 108 km.
1. Quelle relation mathématique permet de calculer une durée en connaissant une distance et une vitesse ?
2. Applique cette formule et donne la durée mise par un signal pour parcourir la distance Terre-Mars.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24-CDistances et durées dans le système solaire. La distance des planètes.
Jean s'intéresse à Neptune, la dernière planète du système solaire, qui sera visible un soir de la semaine. Combien de temps a mis la lumière pour parvenir jusqu'à la Terre et rendre Neptune visible ?
1. Calcule la durée mise par la lumière pour parcourir la distance Neptune-Terre. Exprime-la dans l'unité la plus adaptée.
1. Calcule la durée mise par la lumière pour parcourir la distance Neptune-Terre. Exprime-la dans l'unité la plus adaptée.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
J'approfondis
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Comprendre l'utilité de l'unité année-lumière.
Timothée apprend que la lumière reçue cette nuit sur Terre en provenance de l'étoile Deneb a été émise lors du règne du roi des Burgondes nommé Sigismond, fils de Gondebaud.
1. Effectue une recherche afin de connaitre les dates clés du règne de ce personnage.
2. Déduis-en les durées possibles du trajet de la lumière venant de Deneb.
1. Effectue une recherche afin de connaitre les dates clés du règne de ce personnage.
2. Déduis-en les durées possibles du trajet de la lumière venant de Deneb.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26Les diamètres des planètes.
1. Le tableau suivant donne le pourcentage des diamètres des planètes du système solaire, comparés au diamètre de la Terre. Complète-le.
| Planète | Diamètre | Pourcentage |
| Terre | 13 700 km | 100 % |
| Jupiter | 1,4 x 108 m | |
| Mercure | 4 800 km | |
| Mars | 50 % | |
| Saturne | 875 % | |
| Vénus | 12 700 000 m |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27Valeurs approchées.
Données :
2. Calcule la valeur exacte, puis propose une valeur approchée en secondes de la durée mise par la lumière pour effectuer un aller-retour Terre-Lune.
3. Calcule la valeur exacte, puis propose une valeur approchée en minutes de la durée mise par la lumière émise par le Soleil pour arriver sur la Terre.
4. Propose une valeur approchée en km de la distance Terre-Soleil.
- distance Terre-Lune : 384 000 km
- distance Terre-Soleil : 149 600 000 km
2. Calcule la valeur exacte, puis propose une valeur approchée en secondes de la durée mise par la lumière pour effectuer un aller-retour Terre-Lune.
3. Calcule la valeur exacte, puis propose une valeur approchée en minutes de la durée mise par la lumière émise par le Soleil pour arriver sur la Terre.
4. Propose une valeur approchée en km de la distance Terre-Soleil.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Positions relatives.
1. Où se situe la Terre dans le système solaire ?
2. Où se situe la Lune dans le système solaire ?
3. Où se situe le Soleil dans le système solaire ?
4. Où se situe le système solaire dans la Voie lactée ?
2. Où se situe la Lune dans le système solaire ?
3. Où se situe le Soleil dans le système solaire ?
4. Où se situe le système solaire dans la Voie lactée ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29Laquelle choisir ?
Données :
1. Positionne convenablement le Soleil et les trois planètes citées sur un schéma.
2. Donne la valeur en UA de la distance avec la Terre pour chacune des planètes, dans le cas où elles seraient toutes alignées.
3. En quelle unité faut-il exprimer ces distances pour pouvoir ensuite effectuer des calculs de durée ?
4. Calcule pour chaque planète la durée de propagation de la lumière à partir de la Terre.
5. Quelle est la bonne planète ?
- distance Soleil-Terre = 1 UA
- distance Soleil-Mercure = 0,38 UA
- distance Soleil-Jupiter = 5,20 UA
- distance Soleil-Uranus = 19,20 UA
1. Positionne convenablement le Soleil et les trois planètes citées sur un schéma.
2. Donne la valeur en UA de la distance avec la Terre pour chacune des planètes, dans le cas où elles seraient toutes alignées.
3. En quelle unité faut-il exprimer ces distances pour pouvoir ensuite effectuer des calculs de durée ?
4. Calcule pour chaque planète la durée de propagation de la lumière à partir de la Terre.
5. Quelle est la bonne planète ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30Documentaire.
Compétence
Comprendre et interpréter des tableaux ou des documents graphiques.
Le Soleil ne se situe pas au centre de la trajectoire de la Terre : il est décalé. Lisa se documente et trouve les données suivantes :
- point le plus proche du Soleil (périhélie) = 147,349 millions de km
- point le plus éloigné du Soleil (aphélie) = 152,446 millions de km
Le zoom est accessible dans la version Premium.
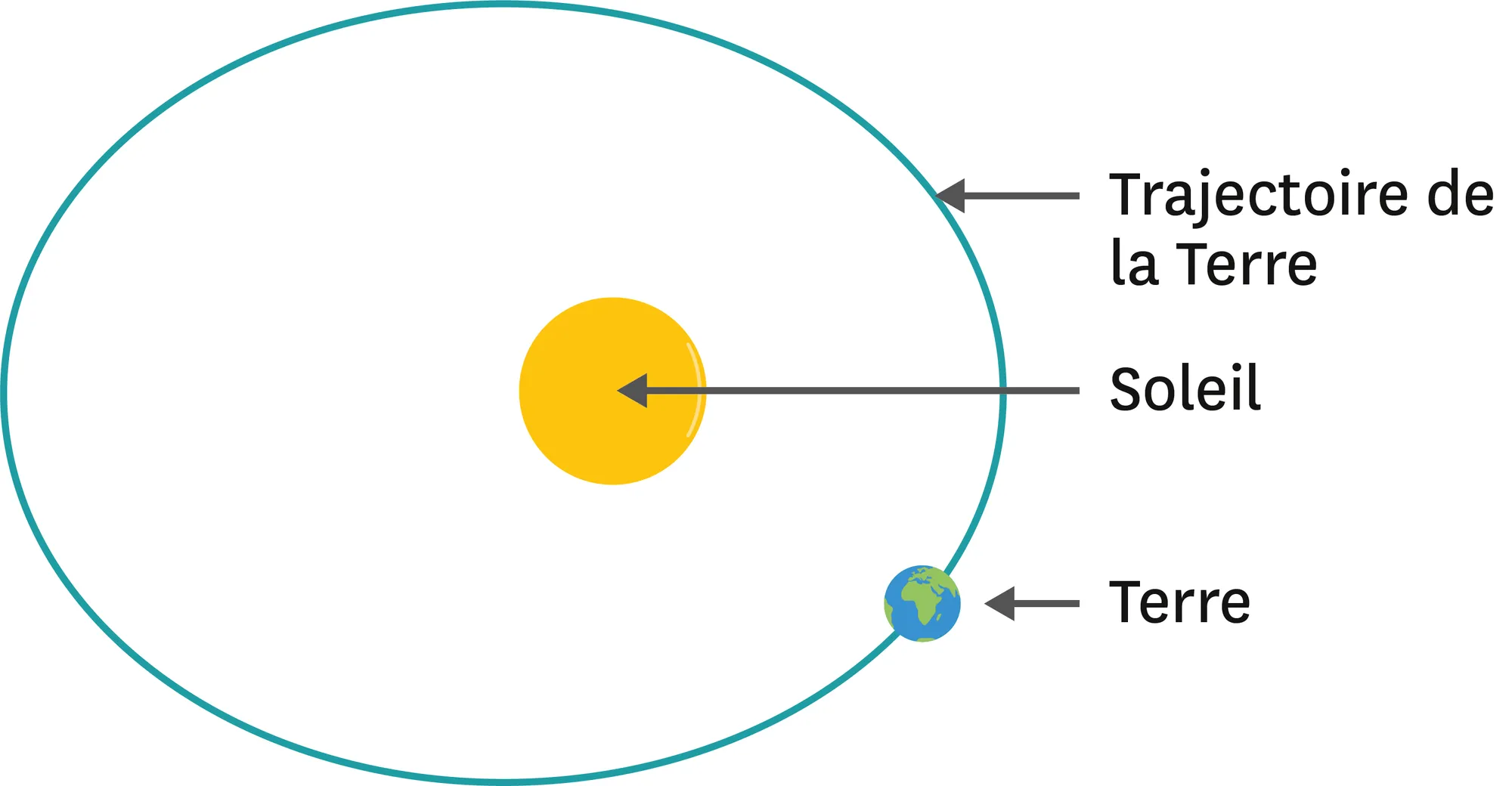
1. Quelle est la conséquence de ce décalage sur la durée de propagation de la lumière du Soleil à la Terre ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31Système solaire.
Compétence
Produire et transformer des tableaux ou des documents graphiques.
1. Reproduis cette représentation artistique en la simplifiant et inscris en légende le nom de chacun des corps célestes représentés.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32Vrai ou faux ?
Lily pense que la lumière diffusée par Neptune met 4 heures et 20 minutes pour arriver sur Terre.
Données :
Données :
- distance Terre-Neptune = 4 545 millions de km
- vitesse de la lumière = 300 000 km/s
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33Faire des conversions.
Vrai ou faux ? Si l'égalité est fausse, corrige-la :
1. 1 km = 1,5 \times 10^8 UA
2. 1,5 \times 10^{10} km = 100 UA
3. 4,5 \times 10^8 km = 3 UA
4. 0,1 UA = 15 000 000 km
5. 0,07 UA = 1,05 \times 10^{18} km
6. 20 UA = 3 108 km
1. 1 km = 1,5 \times 10^8 UA
2. 1,5 \times 10^{10} km = 100 UA
3. 4,5 \times 10^8 km = 3 UA
4. 0,1 UA = 15 000 000 km
5. 0,07 UA = 1,05 \times 10^{18} km
6. 20 UA = 3 108 km
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34Distance Terre-Lune.
La lumière parcourt la distance Terre-Lune en 2,56 secondes.
Données :
2. Propose une échelle adaptée permettant de représenter la Terre et la Lune sur une feuille de format A4.
3. Quelles distances, parmi celles qui suivent, pourraient également être représentées à l'échelle que tu as proposée ?
Données :
- hauteur Tour Eiffel : 300 m
- fleuve Mississipi : 3 780 km
- circonférence terrestre : 40 000 km
2. Propose une échelle adaptée permettant de représenter la Terre et la Lune sur une feuille de format A4.
3. Quelles distances, parmi celles qui suivent, pourraient également être représentées à l'échelle que tu as proposée ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35Calculs de pourcentages.
La durée de vie des hommes et des femmes ne cesse de croitre sur Terre. Cette augmentation de la durée de vie est essentiellement due aux avancées scientifiques. Que représentent 100 ans de vie terrestre par rapport aux durées caractérisant les astres ?
1. Recherche sur internet depuis combien de temps environ le gaz dioxygène est apparu sur Terre.
2. Calcule le pourcentage que représentent 100 ans par rapport à cette durée.
3. Recherche quelle est l'espérance de vie à la naissance en France.
4. Calcule le pourcentage que représentent 100 ans par rapport à cette durée.
5. Que peux-tu déduire de tes réponses aux questions 3 et 4 ?
1. Recherche sur internet depuis combien de temps environ le gaz dioxygène est apparu sur Terre.
2. Calcule le pourcentage que représentent 100 ans par rapport à cette durée.
3. Recherche quelle est l'espérance de vie à la naissance en France.
4. Calcule le pourcentage que représentent 100 ans par rapport à cette durée.
5. Que peux-tu déduire de tes réponses aux questions 3 et 4 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36Éloignement de la Lune.
La Lune s'éloigne en moyenne de 4 cm par an de la Terre.
1. Calcule l'augmentation de la durée du voyage aller-retour pour la lumière.
2. Cette augmentation est-elle mesurable avec un simple chronomètre de sport ? Explique ta réponse.
1. Calcule l'augmentation de la durée du voyage aller-retour pour la lumière.
2. Cette augmentation est-elle mesurable avec un simple chronomètre de sport ? Explique ta réponse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je résous un problème
Compétence : Lire et comprendre des documents scientifiques pour en extraire des informations.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Enzo et Romain veulent faire une frise chronologique originale. Ils vont placer l'année de départ des lumières provenant de différents corps célestes (Doc. 1) et arrivant cette nuit sur Terre sur une frise existante (Doc. 2). Vérifie que chaque corps céleste prévu trouvera bien une place sur la frise.
Comment procéder ? Donne tes réponses.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Tableau indiquant les distances relatives de différents corps célestes-Terre.
Pour les deux dernières cases du tableau, les distances sont estimées par rapport à la Voie lactée et non par rapport à la Terre. Toutefois, cette différence de point d'origine n'est pas perceptible pour la résolution de l'exercice.
| Nom du corps céleste | Distance en km |
| Sirius | 8,1 x 1013 |
| Canopus | 9,2 x 1014 |
| Spica | 2 x 1015 |
| Rigel | 8,5 x 1015 |
| Nuage de Magellan | 1,6 x 1018 |
| Galaxie d'Andromède | 2 x 1019 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Frise historique.
Le zoom est accessible dans la version Premium.
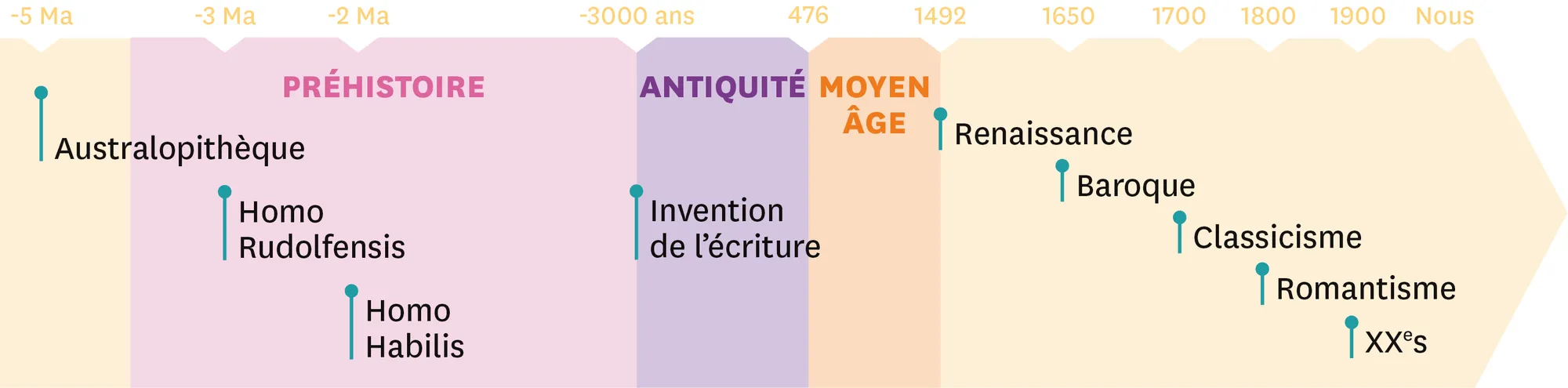
Les échelles de temps ne sont pas respectées, par souci de clarté de la frise.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices supplémentaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37Satellite naturel.
Réponds aux questions ci-dessous. Tu pourras faire des recherches pour compléter les informations que tu connais déjà.
1. Comment s'appelle le satellite naturel de la Terre ?
2. Quelle est la valeur approximative de la distance séparant ce satellite de la Terre ?
3. Quelle est la durée d'une révolution de ce satellite ?
1. Comment s'appelle le satellite naturel de la Terre ?
2. Quelle est la valeur approximative de la distance séparant ce satellite de la Terre ?
3. Quelle est la durée d'une révolution de ce satellite ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38Distance Terre-Soleil et conversions d'unités.
La distance Terre-Soleil vaut 150 millions de kilomètres environ.
Donnée : 1 a.l. = 63 242 UA
1. Écris cette distance en utilisant la notation scientifique (voir l'activité 3) sans changer l'unité.
2. Convertis cette distance en unité astronomique.
3. Convertis cette distance en année-lumière.
4. Quelle unité est la mieux adaptée pour exprimer cette distance ? Pourquoi ?
Donnée : 1 a.l. = 63 242 UA
1. Écris cette distance en utilisant la notation scientifique (voir l'activité 3) sans changer l'unité.
2. Convertis cette distance en unité astronomique.
3. Convertis cette distance en année-lumière.
4. Quelle unité est la mieux adaptée pour exprimer cette distance ? Pourquoi ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Parcours de compétences
Compétence : Effectuer des recherches documentaires.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À l'aide des ressources documentaires dont tu disposes, effectue des recherches sur le thème des éclipses solaires, afin de présenter un exposé de quelques minutes sur le sujet.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 1
Je connais différents outils de recherches.
Coup de pouce
En dehors des sites internet, quels documents peuvent te permettre de faire des recherches sur les éclipses ? Dans ton établissement, où peux-tu trouver ces documents ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 2
J'identifie les informations utiles proposées par un document.
Coup de pouce
Sur une feuille, note les informations trouvées qui te semblent importantes ainsi que leur source. Les informations importantes sont celles mises en valeur (en gras, italique, etc.).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 3
Je collecte les informations utiles en vérifiant la fiabilité de mes sources.
Coup de pouce
As-tu trouvé des informations similaires dans des documents différents ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 4
Je trie de façon pertinente les informations issues de ma recherche en vérifiant la fiabilité de mes sources.
Coup de pouce
Un site institutionnel est plus fiable qu'un site personnel. Si ton information vient d'un journal ou d'un livre, s'agit-il d'un ouvrage de vulgarisation scientifique connu pour son sérieux ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah