Automatisme 15
Recherche d'image et d'antécédents d'un nombre par une fonction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rituel
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retrouvez tous les rituels sur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Soit f la fonction définie par f(x)=x+2.
Calculer f(1).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Soit g la fonction définie par g(x)=x^2. Calculer
l'image de 0 par la fonction g.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Soit h la fonction définie par h(x)=3 x.
Calculer l'antécédent de 5 par la fonction h.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Soit \cal C_f la courbe représentative de la fonction f suivante.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Déterminer graphiquement l'image de 1 par la fonction f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Déterminer graphiquement l'antécédent de 6 par la fonction f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
J'apprends
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Soit f une fonction définie sur un intervalle \mathrm{I}, qui associe à chaque nombre x, appelé antécédent, un unique nombre f(x), appelé image.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
1
Par le calcul
Soit f la fonction définie sur l'intervalle [-2 ; 2] par f(x)=3 x+5.
- Pour calculer l'image de
\red 2 par la fonction f, on remplace x par \red 2 dans l'expression de f(x). f(\red{2})=3 \times \red{2}+5=\blue{11}.
Retrouvez une animation en démonstration
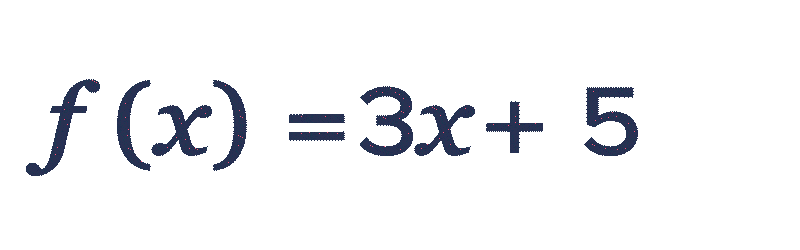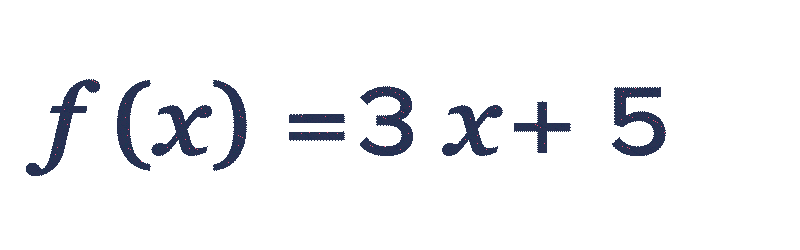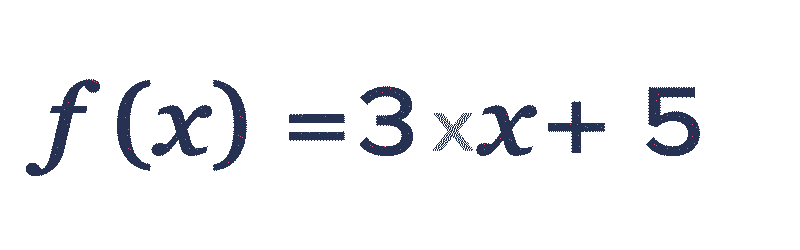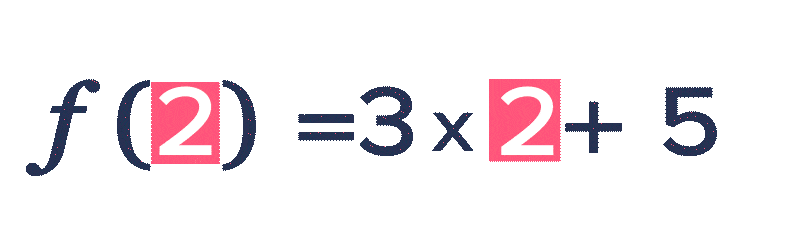
- Pour calculer les antécédents de \blue{8} par la fonction f, on résout l'équation f(x)=\blue{8} et on trouve x = \red{1}.
Retrouvez une animation en démonstration
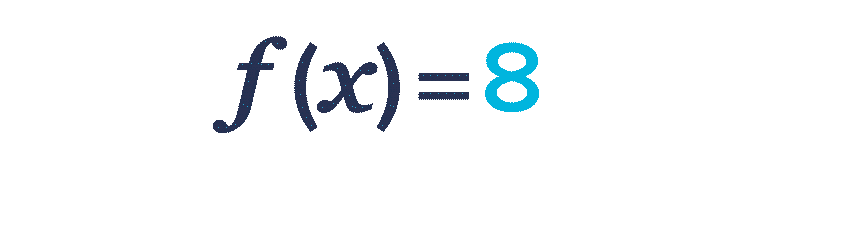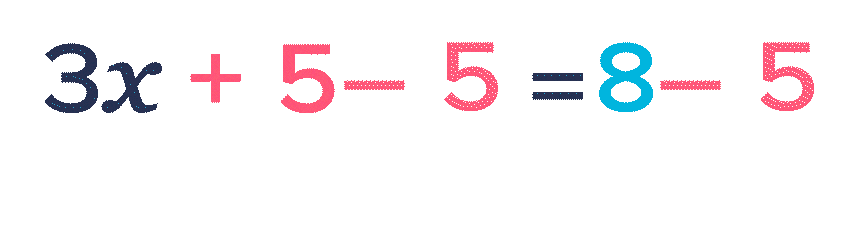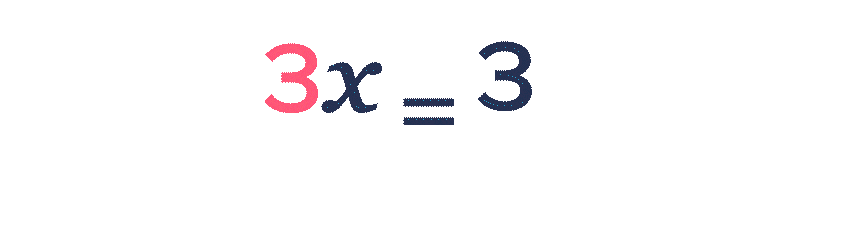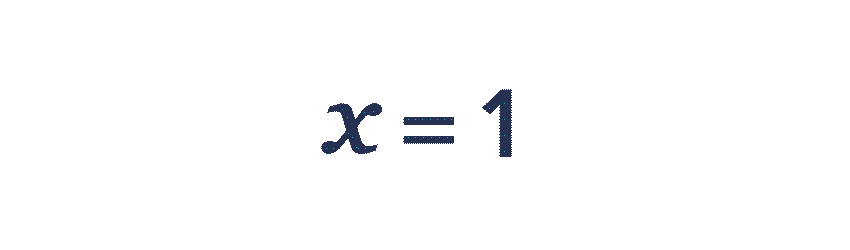
2
Graphiquement
Soit g la fonction dont la représentation graphique est la suivante.

- Pour déterminer l'image de 2 par la fonction g, on lit l'ordonnée du point de la courbe d'abscisse
2 et on trouve g(2)=\red{0,5}.
Retrouvez une animation en démonstration
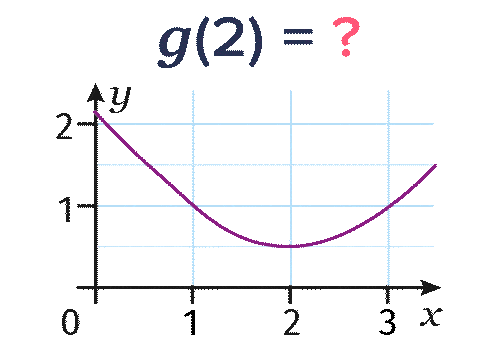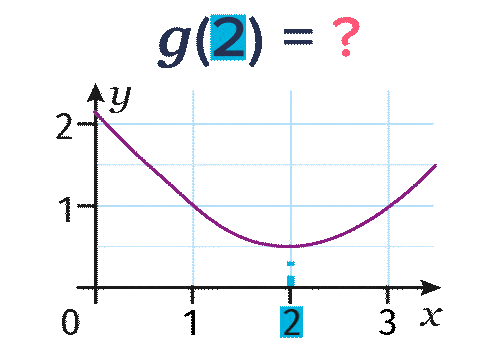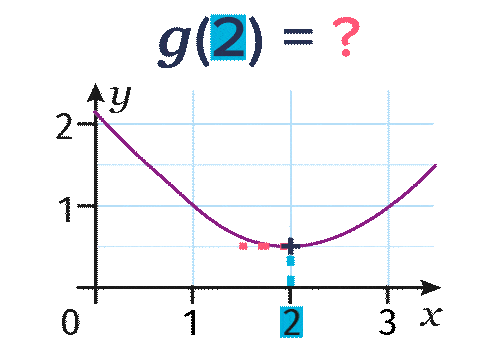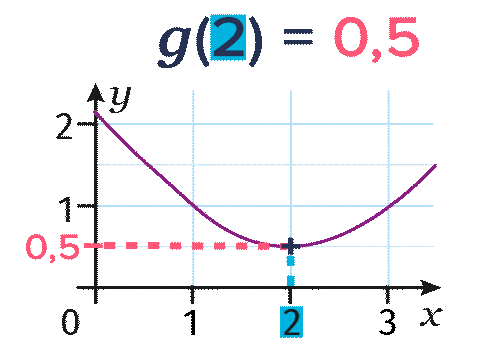
- Pour déterminer les antécédents de 1 par la fonction g, on lit l'abscisse des points de la courbe d'ordonnée 1 et on trouve g(\blue{1})=1 et g(\blue{3})=1.
Retrouvez une animation en démonstration
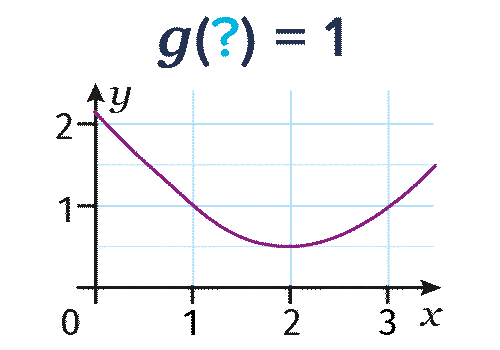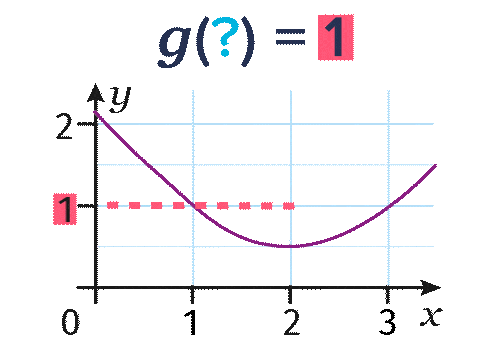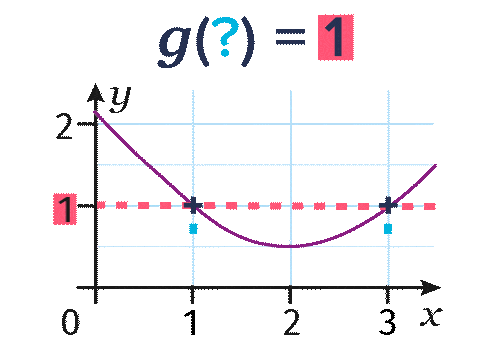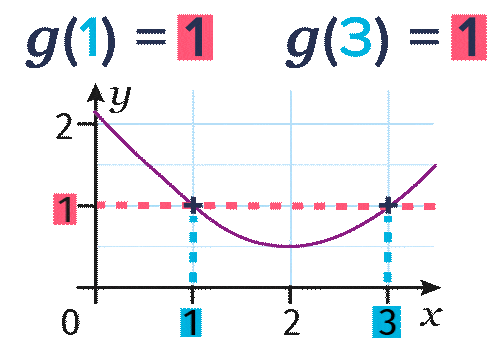
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je m'entraîne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Soit f la fonction définie sur [-1 ; 5] par f(x)=2 x+8.
1. Calculer l'image de 3 par la fonction f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
On considère les représentations graphiques \cal C_f et \cal C_g des fonctions f et g ci-dessous.

1.
Déterminer graphiquement l'image de 2 par la fonction f.
2.
Déterminer graphiquement l'image de 1 par la fonction g.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Soit f la fonction définie sur \R par f(x)=5 x+2.
1. Calculer un antécédent de 62 par la fonction f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
On considère les représentations graphiques \cal C_f et \cal C_g des fonctions f et g ci-dessous.

1. Déterminer graphiquement le (ou les) antécédent(s) de 1 par la fonction f.
2.
Déterminer graphiquement le (ou les) antécédent(s) de -1 par la fonction g.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille





