Méthode
Décryptage du programme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'enseignement explicite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que dit le programme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
« L'enseignement explicite des attendus, notamment en calcul et en résolution de problèmes, doit [...] permettre [aux élèves]
de réaliser les tâches proposées, d'abord en étant guidés par l'enseignant, puis en devenant progressivement autonomes, en
travaillant seuls ou en collaborant avec d'autres élèves. La mise en activité des élèves est donc recherchée à chaque occasion
qui s'y prête, en veillant à ce qu'elle ne conduise pas à réduire les attentes du programme en termes d'objectifs d'apprentissage.
Les progrès et les réussites des élèves donnent lieu à des encouragements et des félicitations de la part de l'enseignant : ce sont
des facteurs essentiels pour entretenir l'estime de soi, la motivation et la dynamique de progrès des élèves. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que propose cette méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La cible de la séance
Chaque séance débute par
la présentation de l'objectif
d'apprentissage, pour aider les
élèves à prendre conscience
de ce qu'ils vont apprendre.
Afin d'aider tous les élèves
à garder en tête cet objectif,
il est matérialisé par un
pictogramme en forme de
cible. Ce moment-clé est
systématiquement repris en
fin de séance.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le bilan en trois temps
À la fin de chaque séance, un
bilan collectif en deux ou trois
temps est organisé. Les élèves
sont amenés à s'interroger sur
leur réussite de l'activité, à
mettre en lumière les stratégies
mathématiques utilisées, et
à développer une réflexion
métacognitive, afin de les aider à
réfléchir à leurs apprentissages,
à faire des liens, et à analyser ce
qu'ils ont compris.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La qualité
de la verbalisation
Une grande attention est portée
à la précision de la verbalisation
de l'enseignant : les consignes
sont systématiquement rédigées
avec des formulations efficaces
pour les élèves. Par ailleurs,
des temps de verbalisation
de la pensée des élèves sont
aménagés, en favorisant
notamment les échanges à deux à chaque séance.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La mise en activité des élèves
La mise en activité des élèves
est pensée tout au long des
séquences via différentes
modalités : travail en groupes,
travail individuel et travail
collectif sont proposés à chaque
séance. Les temps collectifs sont
pensés pour rendre tous les
élèves actifs, en leur permettant
de s'engager individuellement
par la parole ou par le corps.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le journal d'apprentissage
Proposé à la fin de chaque séquence, le
journal d'apprentissage permet aux élèves
de prendre conscience de ce qu'ils ont
appris. Grâce à une consigne ouverte,
ils organisent et relient leurs connaissances,
et réfléchissent à leurs apprentissages.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La résolution de problèmes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que dit le programme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
« Pour être en capacité de résoudre des problèmes, il faut savoir prendre
des initiatives, imaginer des pistes de solution et s'y engager sans s'égarer.
Un moyen pour y parvenir consiste à procéder par analogie en rattachant
une situation particulière à une classe plus générale de problèmes. [...]
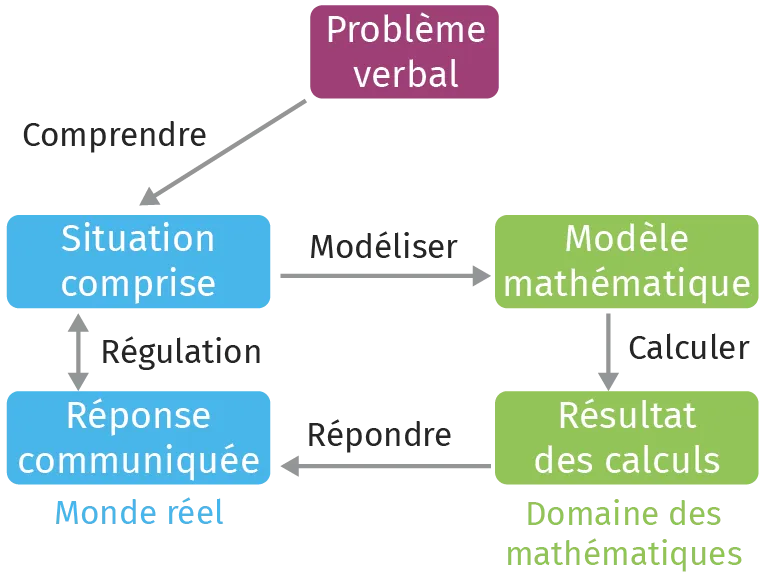
La résolution de problèmes arithmétiques fait l'objet d'un enseignement
explicite. Celui-ci s'appuie sur le modèle de résolution de problèmes en
quatre phases synthétisé par le schéma ci-contre. Il constitue notamment
un outil utile à l'enseignant pour identifier l'étape de la résolution sur
laquelle un élève est en difficulté.
Les élèves doivent traiter au moins dix problèmes par semaine, une partie d'entre eux pouvant être des problèmes élémentaires, à l'énoncé bref, proposés oralement, la réponse étant simplement notée sur l'ardoise. »
Les élèves doivent traiter au moins dix problèmes par semaine, une partie d'entre eux pouvant être des problèmes élémentaires, à l'énoncé bref, proposés oralement, la réponse étant simplement notée sur l'ardoise. »

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que propose cette méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La résolution de problèmes
au cœur des apprentissages
Un apprentissage explicite et systématique
de la résolution de problèmes est proposé
aux élèves lors de séances dédiées. Par
ailleurs, les élèves sont fréquemment mis en
situation de résolution de problèmes dans
différentes situations d'apprentissage et via
des rituels de début de séance. Les élèves
apprennent donc à résoudre des problèmes,
mais ils apprennent également en résolvant
des problèmes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problèmes de référence
et variations
Pour chaque type de problème mentionné dans le programme, les élèves
découvrent et résolvent un problème de
référence auquel ils pourront rattacher
les autres problèmes rencontrés. Après
avoir résolu le problème de référence, les
élèves sont confrontés à des variations
de ce problème, puis à des problèmes du
même type.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10 problèmes par semaine
Un rituel quotidien de
« problèmes du jour » permet,
en plus des séances dédiées,
d'atteindre aisément cet
objectif hebdomadaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Donner du sens
Pour chaque problème, les élèves sont amenés à
se questionner sur la cohérence de leur résultat à
travers une phase de régulation, au cours de laquelle
ils se demandent si le résultat est plausible.
À chaque période, des problèmes « en plein air » sont
proposés afin de permettre aux élèves de poursuivre
la construction de leurs compétences à partir de
situations issues du réel, ce qui renforce le lien entre
les séances de mathématiques et la vie quotidienne.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une banque
de problèmes numérique
Sur , une banque de
problèmes est accessible gratuitement.
Elle comporte de nombreux énoncés de
problèmes sous des formats originaux
(audio, vidéo, animations, etc.)




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Manipuler - Représenter - Abstraire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que dit le programme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
« Dans la continuité de l'enseignement dispensé à l'école maternelle, l'enseignement des mathématiques au cycle 2 repose
sur une approche menant progressivement du concret à l'abstrait, en passant par la représentation imagée. Les élèves
manipulent des objets tangibles (matériel de numération, surfaces de différentes formes représentant des fractions,
bandes de papier, ficelles, monnaie fictive, etc.) pour s'approprier de manière concrète le sens de notions mathématiques
(numération, fractions, nombres décimaux, etc.) et de procédures qui s'y appliquent (comparaison, ajout, retrait, groupement,
partage, etc.). Ils passent ensuite à la représentation schématisée de ces objets et de ces actions, avant d'accéder au langage
mathématique (écriture décimale ou fractionnaire, symboles opératoires ou géométriques, etc.). Ce passage progressif
du concret à l'abstrait suscite cependant plusieurs points de vigilance. Tout d'abord, si la manipulation est un passage
essentiel, la réussite d'une activité manipulatoire ne suffit cependant pas pour attester de la compréhension de la notion
mathématique qui la sous-tend. Pour que les phases de manipulation et de représentation permettent l'accès à l'abstraction,
il importe notamment que les procédures engagées soient verbalisées, à la fois par les élèves eux-mêmes, avec leurs propres
mots, et par l'enseignant, avec le vocabulaire adapté. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que propose cette méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Manipuler régulièrement
Des phases de manipulation
sont organisées au sein de
chaque séquence afin de
permettre à tous les élèves de
donner du sens aux concepts
mathématiques travaillés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Manipuler activement
Les élèves ne sont pas simplement
mis en contact avec du matériel.
Celui-ci leur sert pour la formulation
d'hypothèses et puis, si nécessaire,
pour la vérification du résultat :
c'est la condition de l'efficacité de la
manipulation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Manipuler en jouant
Les séquences contiennent très
régulièrement des phases de
jeu incluant de la manipulation.
Ces jeux sont faciles à mettre en
place et permettent de rendre les
élèves actifs rapidement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Du matériel standard
En dehors du matériel
détachable fourni dans le
fichier, cubes emboitables et
jetons sont les objets les plus
couramment utilisés lors des
séances.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Verbaliser à toutes les étapes
C'est en accompagnant chaque étape de l'activité par le langage
que l'on amène les élèves à la construction des concepts
mathématiques. Les élèves sont encouragés, à chaque séance,
à expliciter leurs actions, à anticiper leurs résultats et à formuler
des hypothèses en échangeant avec des camarades. Pour
l'enseignant, des exemples de verbalisations sont proposés à
chaque moment d'apprentissage. Les concepts mathématiques
en jeu sont clarifiés au début de chaque séance afin d'aider
l'enseignant à se repérer dans les notions travaillées et à
employer le vocabulaire pertinent.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Avancer avec tous les élèves
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que dit le programme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
« Afin de s'assurer d'une bonne maitrise des attendus à la fin de chaque année scolaire, il est indispensable d'aborder
les notions centrales, et notamment les plus délicates, suffisamment tôt dans l'année scolaire afin de permettre aux élèves,
en particulier aux plus fragiles, de disposer de suffisamment de temps pour acquérir ces notions. Cela implique d'aborder
dès le début d'année scolaire les notions du programme correspondant au niveau de la classe, sans proposer de séquences
qui seraient uniquement consacrées à la révision de notions relevant des années précédentes. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que propose cette méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Des séances
accessibles à tous
Les dispositifs de travail
proposés sont pensés pour
permettre à tous les élèves
de s'engager dans les
apprentissages. La diversité
des sollicitations des élèves,
avec notamment un fort
appui visuel (pictogrammes,
diaporamas, manipulations)
permet de soutenir l'attention
et la compréhension de tous.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Permettre aux élèves de choisir
À chaque fois que les élèves travaillent dans
leur fichier, au moins un exercice propose
d'utiliser du matériel, de travailler en
binôme ou de choisir entre deux versions
d'un exercice. Ces modalités permettent
aux élèves de s'engager davantage dans
les tâches demandées et d'être rassurés
dans la réalisation de leur travail.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une place pour chacun
Développer quasi quotidiennement
les échanges au sein de binômes
permet de favoriser les prises de
parole de chacun. Tous les élèves
sont incités à exposer leur point de
vue et doivent se sentir légitimes
à le faire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Des propositions alternatives
Des activités à destination des élèves éprouvant des
difficultés sont régulièrement proposées, tout comme
des pistes pour les élèves plus rapides : travail écrit
adapté, proposition alternative de mise en œuvre et
compléments et exercice bonus en bas de page du fichier.




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La fluence de calcul
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que dit le programme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
« Pour le calcul mental, il s'agit d'une part de définir un ensemble de procédures fondamentales que tous les élèves doivent
maitriser, mais aussi de proposer des indicateurs de maitrise. En effet, tout comme "savoir lire" ne signifie pas la même chose
en CP et en CE2 concernant le nombre de mots lus en une minute, "connaitre les tables d'addition" ne correspond pas aux
mêmes attendus en CP et en CE2 concernant le nombre de résultats que les élèves sont capables de restituer en une minute
[...]. Cette mesure de la fluence en calcul mental permet en outre à chaque élève de prendre conscience de ses progrès. Il
convient d'entrainer régulièrement les élèves à de tels tests afin d'en faire de véritables routines intégrées aux apprentissages,
n'engendrant plus de stress, et permettant de valoriser les progrès réalisés afin de renforcer la confiance en soi et la réussite
de chacun. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que propose cette méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Un entrainement
quotidien au calcul
Chaque séance débute par un
rituel de calcul de 10 minutes.
Celui-ci permet de travailler la
mémorisation des faits numériques, mais aussi de s'exercer aux procédures
apprises tout
au long de l'année.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Des tests réguliers de fluence
À partir de la 5e
semaine de
l'année, un test de fluence
proposé toutes les deux semaines
est
en lieu et place du rituel de calcul
Conformément au programme,
.
ces tests réguliers permettent à la
fois de faire progresser les élèves
et de les habituer à ce format en
temps limité. Il est important de
dédramatiser cet exercice
qu'il soit abordé




Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Des repères de progression
À l'issue de chaque séance de fluence,
l'élève pourra constater d'un coup
d'œil ses progrès dans son fichier.
Des repères pour atteindre les
objectifs chiffrés du programme sont
également fournis.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Des ressources numériques
supplémentaires
En supplément des pages en fin de
fichier, des fiches-réponses pour les
tests de fluence sont .
On y retrouve également des copies
des pages du fichier pour les élèves
ayant oublié le leur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'égalité fille - garçon
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que dit le programme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
« Les progrès et les réussites des élèves donnent lieu à des encouragements et des félicitations de la part de l'enseignant :
ce sont des facteurs essentiels pour entretenir l'estime de soi, la motivation et la dynamique de progrès des élèves. La mise
en activité, la qualité des échanges avec l'enseignant et avec les autres élèves, la confiance en ses capacités à réussir sont
autant de facteurs qui contribuent au plaisir de faire des mathématiques. Ce sentiment positif doit être éprouvé par tous les
élèves. Au-delà de ce qui a été mentionné pour le calcul mental, l'enseignant veille, par le choix des situations qu'il propose,
le regard qu'il porte sur chacun de ses élèves et les opportunités qu'il leur offre de s'exprimer, à favoriser l'égalité entre les
filles et les garçons. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que propose cette méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Des situations le plus souvent neutres
Le moyen le plus efficace de ne pas véhiculer
de stéréotype et de permettre aux élèves
de se concentrer uniquement sur la nature
mathématique d'un problème est de le rendre
neutre, par exemple en mettant en scène des
objets ou des animaux : c'est le choix que
nous avons privilégié.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Des situations dépourvues
de stéréotypes
Dans toutes les activités ainsi que
dans tous les énoncés mettant
en scène des enfants, nous avons
veillé à ne pas perpétuer les
nombreux stéréotypes de genre
présents dans la vie de tous les
jours, et parfois
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Un travail d'inter-reconnaissance
La plupart des séances invitent à travailler
en binôme, en échangeant les rôles s'ils
sont différents. Ceci contribue à mettre
tous les élèves sur un pied d'égalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce que l'enseignant peut mettre en place dans la classe
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Prendre conscience
des biais de genre
« Est-ce que j'interroge autant
les filles que les garçons ? À qui
est-ce que je demande de lire
les consignes ? Qui est invité
à présenter ses stratégies ? »
Autant de questions à se poser
pour ne pas assigner nos élèves
à un genre ou à un type de
tâche genrée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Donner une image mixte
de la culture scientifique
La culture scientifique actuelle
est très centrée autour des
hommes scientifiques illustres
et s'adresse plus généralement
aux garçons. Mettre en avant
de façon régulière des femmes
scientifiques est une façon de
contrebalancer ce phénomène.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Combattre le phénomène de
« menace du stéréotype »
De récentes recherches ont montré
qu'une catégorie victime d'un
stéréotype risque beaucoup plus
de réaliser ce stéréotype à cause de
la pression qu'il exerce. Plusieurs
expériences montrent aussi qu'il
« suffit » parfois d'une simple phrase
pour désamorcer le stéréotype des
femmes et des mathématiques et
améliorer leur réussite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

