Annexes
La typologie de problèmes de la méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Il existe plusieurs manières de distinguer les différents types de problèmes en mathématiques.
Dans cette méthode, nous avons choisi de proposer une typologie légèrement simplifiée pour être
accessible par tous les enseignants. C'est ce que nous présentons sur cette page. Les élèves n'ont
pas à connaitre cette typologie. Néamoins, ils doivent apprendre à attribuer à chaque problème une
méthode de résolution, en se référant éventuellement aux différentes affiches réalisées en classe.
En CP, nous étudions deux grandes familles de problèmes : les problèmes additifs et les problèmes multiplicatifs. Dans chacune de ces familles, on distingue les types suivants.
En CP, nous étudions deux grandes familles de problèmes : les problèmes additifs et les problèmes multiplicatifs. Dans chacune de ces familles, on distingue les types suivants.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les problèmes additifs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce sont des problèmes où l'opération sous-jacente est une addition ou une soustraction. Il s'agit de situations dans lesquelles
des quantités s'ajoutent ou se retranchent, une ou plusieurs fois.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Recherche d'un tout
Il s'agit des problèmes où on additionne deux quantités. On peut distinguer
les nuances suivantes, qui se schématisent de la même façon.

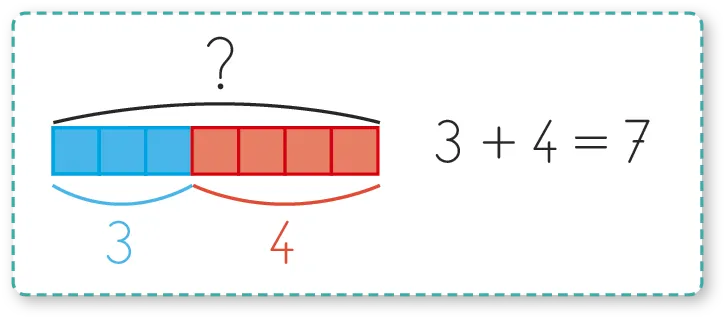


- Problèmes de type « partie-tout » :
Ici, les deux quantités sont toutes les deux présentes en même temps et on les rassemble.ExempleDans la corbeille à fruits, il y a 17 abricots et 9 pêches. Combien de fruits y a-t-il dans la corbeille ?
- Problèmes de type « transformation » :
Ici, c'est un élément temporel qui rassemble les quantités. On peut encore distinguer deux sous-nuances, la seconde étant une source très fréquente d'erreur pour les élèves, qui cherchent souvent à écrire une soustraction.Exemple- transformation « positive » : Il y a un mois, le lapin de Jade mesurait 12 cm. Aujourd'hui il mesure 4 cm de plus. Quelle taille mesure le lapin de Jade aujourd'hui ?
- transformation « négative » : Eva a mangé 16 cerises. Il reste encore 22 cerises. Combien y en avait-il avant qu'Eva n'en mange ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Recherche d'une partie
Il s'agit des problèmes où l'on recherche la partie d'un tout. Ils se résolvent nécessairement par une soustraction. Ici, encore plusieurs nuances existent.

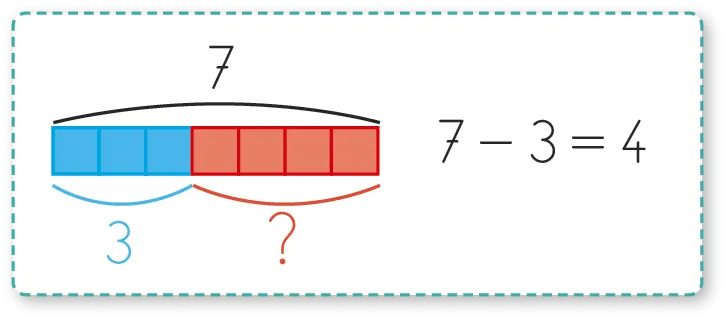


- Problèmes de type « partie-tout » :
ExempleSur l'arbre, il y a 15 oiseaux dont plusieurs moineaux et 7 hirondelles. Combien de moineaux sont sur cette branche ?
- Problèmes de type « transformation » :
Beaucoup de combinaisons sont possibles. En voici 4 différentes.Exemple- On ajoute 2 pommes dans un panier et il y a maintenant 6 fruits. Combien y avait-il de fruits avant que l'on ajoute les pommes ?
- Un coiffeur a reçu 9 clients ce matin. Dans la journée, il en a reçu 25 en tout. Il se demande combien il a eu de clients dans l'après-midi.
- Dans le métro, il y a 19 passagers. Au premier arrêt, 7 personnes descendent. Combien de personnes y a-t-il dans le métro maintenant ?
- Dans le verger, on a récupéré 3 kg de poires hier. Avec la récolte d'aujourd'hui, on a récupéré 8 kg en tout. Combien de kilogrammes de poires a-t-on récupérés aujourd'hui ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
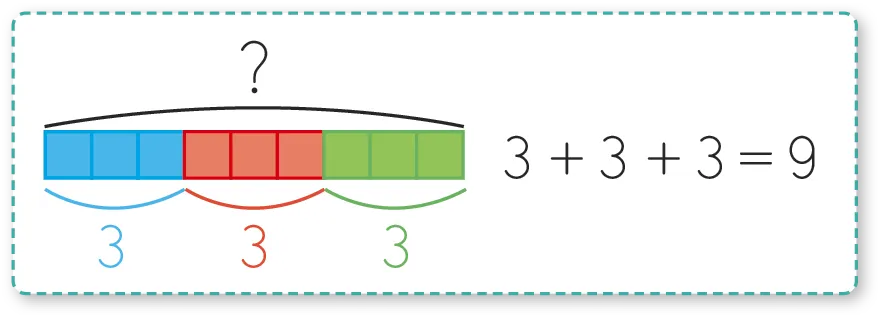
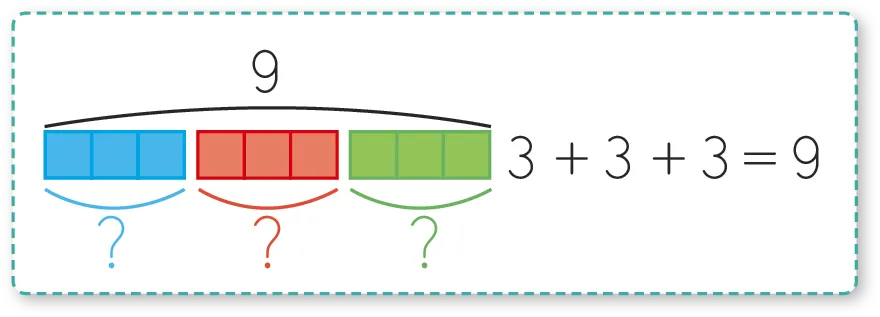
Les problèmes à deux étapes
Dans ces problèmes, il y a deux étapes avant d'arriver au résultat.
La résolution passe donc par deux additions, deux soustractions
ou une de chaque.




Exemple
Il y a 5 personnes dans un bus. Au premier arrêt, 6 voyageurs montent et au deuxième arrêt, 9 personnes de plus montent. Combien
y a-t-il de voyageurs dans le bus après le deuxième arrêt ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les problèmes multiplicatifs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ce sont des problèmes dans lesquels une quantité est répartie en différents groupes de même taille. Ils impliquent donc une
multiplication ou une division. Bien que ces opérations ne soient pas enseignées en CP, ce type de problème est introduit
au CP pour commencer à les construire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Recherche du produit
Il s'agit de trouver la quantité totale lorsqu'on a formé différents groupes
de même taille.



Exemple
Combien de tables y a-t-il dans une
classe organisée en 6 rangées de 4 tables ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Recherche de la valeur d'une part
Ici, on connait le nombre de paquets et le total, et on cherche combien il
y a dans chaque paquet.



Exemple
Un jeu de 28 cartes doit être distribué entre
7 joueurs. Combien de cartes chaque joueur va-t-il avoir ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Recherche du nombre de part
À l'inverse, ici on recherche combien de paquets on doit faire.



Exemple
Iyad a 21 crayons qu'il veut ranger dans
des boites de 7. De combien de boites a-t-il besoin ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

