Chapitre 5
Entrée en matière
Demi-droites graduées
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des mathsDemi-droites graduées et opérations
Une des premières apparitions modernes des demi-droites graduées date du mathématicien anglais John Wallis (1616-1703).
À cette époque, il s'en sert surtout pour faire des calculs. Avec ces axes gradués, il peut faire des additions, des soustractions et même des multiplications et divisions ! Pour expliquer l'opération 5 − 2 avec la figure ci-dessus, Wallis explique qu'il faut imaginer quelqu'un parcourir 5 pas vers la droite en partant de \text{A}, puis reculer de 2 pas vers la gauche. On voit alors que cela revient à avoir fait 3 pas vers la droite : 5 − 2 = 3.
Malgré son apparente simplicité, la notion de demi-droite graduée est fondamentale en mathématiques et s'est développée jusqu'au XIXe siècle.

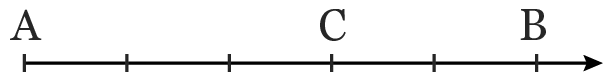
À cette époque, il s'en sert surtout pour faire des calculs. Avec ces axes gradués, il peut faire des additions, des soustractions et même des multiplications et divisions ! Pour expliquer l'opération 5 − 2 avec la figure ci-dessus, Wallis explique qu'il faut imaginer quelqu'un parcourir 5 pas vers la droite en partant de \text{A}, puis reculer de 2 pas vers la gauche. On voit alors que cela revient à avoir fait 3 pas vers la droite : 5 − 2 = 3.
Malgré son apparente simplicité, la notion de demi-droite graduée est fondamentale en mathématiques et s'est développée jusqu'au XIXe siècle.

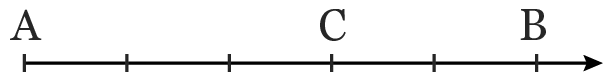
Comment calculer la multiplication de deux entiers sur une demi-droite graduée ?
Supplément numérique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les maths, à quoi ça sert ?
De nos jours, on utilise par exemple les demi-droites graduées sur des thermomètres pour
lire la température, ou bien dans les avions
qui disposent d'instruments gradués pour
vérifier l'inclinaison de l'avion, la vitesse,
l'altitude, etc. Les verres mesureurs possèdent
des graduations pour faciliter la mesure
d'ingrédients lorsque l'on fait la cuisine et, bien
évidemment, on utilise une règle graduée pour
mesurer des longueurs.

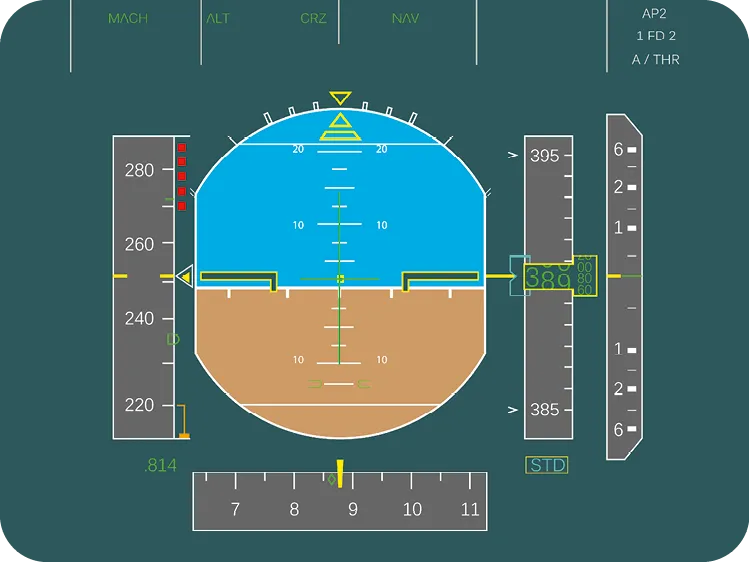
Instruments de bord d'un avion de ligne.


Instruments de bord d'un avion de ligne.
Quelle température peut-on lire sur le
thermomètre ci-dessous ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationUtilisation d'un guide-âne
Pour réaliser cette activité, utiliser .
Cette activité est à faire en groupe ou en classe entière.
Chaque élève dispose d'un guide-âne ainsi que de plusieurs bandelettes de papier.
1. On souhaite partager le segment dessiné sur une bandelette en dix segments égaux en utilisant le guide-âne.
a. Placer la première extrémité du segment sur la ligne 0 et la seconde extrémité sur la ligne 10 (Figure 1).
b. Poser une règle sur chacune des lignes du guide-âne en traçant un trait de graduation à l'intersection avec le segment (Figure 2).
c. Vérifier qu'on obtient bien dix graduations régulières.
2. Si le grand segment correspond à une unité, à quelle fraction d'unité correspond chaque petit segment?

 Figure 1
Figure 1

 Figure 2
Figure 2
3. Procéder de la même façon pour graduer un segment en quatre segments égaux, puis en
sept. Dans chaque cas, dire à combien d'unités correspond chaque petit segment obtenu.
On souhaite graduer une unité de 0,2 en 0,2. Comment doit-on utiliser le guide-âne ?
Chaque élève dispose d'un guide-âne ainsi que de plusieurs bandelettes de papier.
1. On souhaite partager le segment dessiné sur une bandelette en dix segments égaux en utilisant le guide-âne.
a. Placer la première extrémité du segment sur la ligne 0 et la seconde extrémité sur la ligne 10 (Figure 1).
b. Poser une règle sur chacune des lignes du guide-âne en traçant un trait de graduation à l'intersection avec le segment (Figure 2).
c. Vérifier qu'on obtient bien dix graduations régulières.
2. Si le grand segment correspond à une unité, à quelle fraction d'unité correspond chaque petit segment?




Bilan
On souhaite graduer une unité de 0,2 en 0,2. Comment doit-on utiliser le guide-âne ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ActivitéLire des fractions sur une demi-droite graduée
On considère la demi-droite graduée suivante d'origine \text{O}.


1. a. En combien de parts est partagée l'unité ?
b. La distance entre l'origine et chacun des points s'appelle l'abscisse et se note entre parenthèses. Ainsi, l'abscisse du point \text{A} est \frac{1}{7} et on note \text{A} \left ( \frac{1}{7} \right ) .
Déterminer l'abscisse des points \text{B}, \text{C} et \text{D}.
2. À l'aide du point \text{B} sur le schéma précédent, justifier que \frac{8}{7}=1+\frac{1}{7}. Comment s'appelle cette écriture ?
3. Donner des égalités similaires pour les abscisses de \text{C} et \text{D}.
Donner une méthode pour lire des fractions sur une droite graduée.


1. a. En combien de parts est partagée l'unité ?
Bilan
Donner une méthode pour lire des fractions sur une droite graduée.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille