Chapitre 5
Cours
Demi-droites graduées
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Repérage
Définition
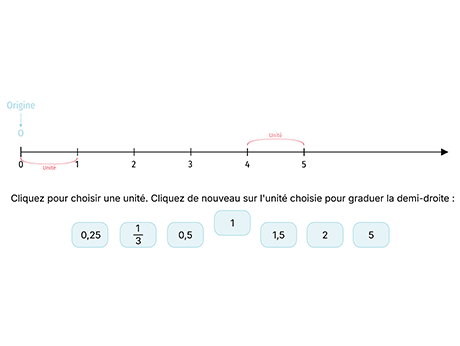
Une demi-droite graduée est une demi-droite pour laquelle on a choisi une unité de longueur que l'on a reportée régulièrement depuis l'origine, souvent notée \text{O}.
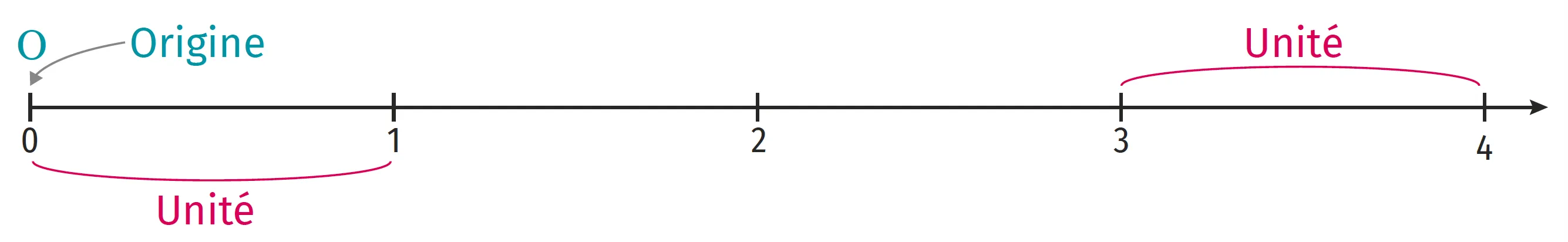
- On trace le plus souvent une demi-droite graduée à l'horizontale, avec l'origine à gauche.
- Le sens de la demi-droite est donné par la connaissance de deux graduations, généralement le 0 et le 1.
Propriété
Sur une demi-droite graduée, chaque point est repéré par un unique nombre appelé abscisse de ce point. Réciproquement, chaque nombre est l'abscisse d'un unique point de la demi-droite.
- L'origine de la demi-droite graduée a pour abscisse 0.
- On note l'abscisse d'un point entre parenthèses.
Exemples :
1. Sur la demi-droite graduée ci-dessous, l'unité est partagée en quatre parts égales.
L'abscisse de \text{A} est 0,25, l'abscisse de \text{B} est 0,5, l'abscisse de \text{C} est 2 et l'abscisse de \text{D} est 2,75. On note donc : \text{A} \left (0,25 \right), \text{B} \left ( 0,5 \right ) , \text{C} \left ( 2 \right ) et \text{D} \left ( 2,75 \right ).
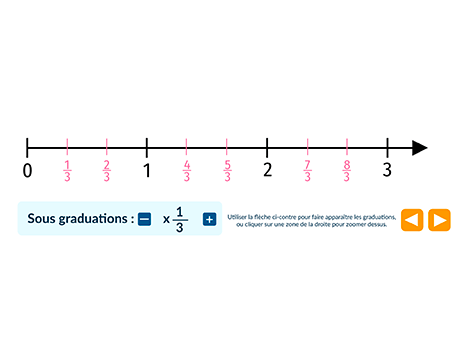
2. Sur la demi-droite graduée ci-dessous, l'unité est partagée en trois parts égales.
On lit que l'abscisse du point \text{E} est égale à \frac{6}{3}=2. L'abscisse du point \text{F} est égale à \frac{10}{3}.
On note alors \text{E} \left ( 2 \right ) et \text{F} \left ( \frac{10}{3} \right ).
1. Sur la demi-droite graduée ci-dessous, l'unité est partagée en quatre parts égales.
L'abscisse de \text{A} est 0,25, l'abscisse de \text{B} est 0,5, l'abscisse de \text{C} est 2 et l'abscisse de \text{D} est 2,75. On note donc : \text{A} \left (0,25 \right), \text{B} \left ( 0,5 \right ) , \text{C} \left ( 2 \right ) et \text{D} \left ( 2,75 \right ).
2. Sur la demi-droite graduée ci-dessous, l'unité est partagée en trois parts égales.
On note alors \text{E} \left ( 2 \right ) et \text{F} \left ( \frac{10}{3} \right ).
Sur une demi-droite graduée, l'ordre des points dans le sens de la flèche correspond à l'ordre croissant de leur abscisse. Ici, comme \text{E} est à gauche de \text{F}, on a 2 \lt \frac{10}{3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Applications
Définition
Encadrer un nombre revient à trouver deux autres nombres tels que l'un lui est inférieur et l'autre lui est supérieur.
Exemples :
1. On place le nombre 27 sur la demi-droite graduée ci-dessous.
On constate que le nombre 27 est entre les nombres 20 et 30. On écrit alors 20 \lt 27 \lt 30. Le nombre 27 est ainsi encadré à la dizaine près.
2. On place le nombre \frac{12}{7} sur la demi-droite graduée ci-dessous.
On constate que le nombre \frac{12}{7} est entre les nombres 1 et 2. On écrit alors 1 \lt \frac{12}{7} \lt 2. Le nombre \frac{12}{7} est ainsi encadré à l'unité près.
On constate que le nombre 27 est entre les nombres 20 et 30. On écrit alors 20 \lt 27 \lt 30. Le nombre 27 est ainsi encadré à la dizaine près.
2. On place le nombre \frac{12}{7} sur la demi-droite graduée ci-dessous.
On constate que le nombre \frac{12}{7} est entre les nombres 1 et 2. On écrit alors 1 \lt \frac{12}{7} \lt 2. Le nombre \frac{12}{7} est ainsi encadré à l'unité près.
Définition
Intercaler un nombre entre deux autres revient à trouver un nombre compris entre les deux nombres donnés.
Exemple :
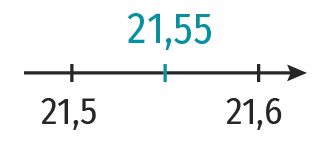
On souhaite intercaler un nombre entre 21,5 et 21,6. En utilisant la
demi-droite graduée ci-contre, on constate qu'il existe une infinité de
possibilités. On peut par exemple intercaler 21,55 entre 21,5 et 21,6.
Les nombres 21,51 et 21,502 sont d'autres possibilités.
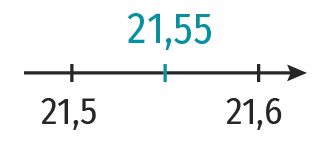
Définition
Arrondir un nombre, c'est donner le nombre le plus proche avec la précision demandée. On peut trouver cet arrondi en trouvant de quel nombre il est le plus proche sur une demi-droite graduée.
Exemple :
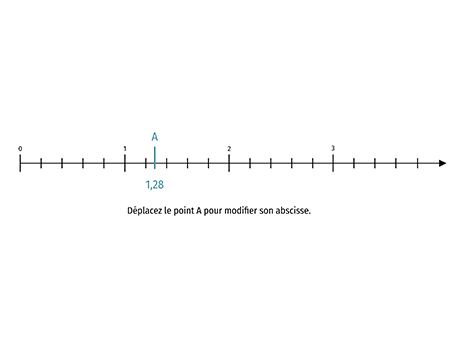
Le point \text{A} d'abscisse 14,569 est plus proche du point d'abscisse 15 que du point d'abscisse 14. On en déduit que l'arrondi à l'unité de 14,569 est 15. De même, l'arrondi au dixième de 14,569 est 14,6.
Le point \text{A} d'abscisse 14,569 est plus proche du point d'abscisse 15 que du point d'abscisse 14. On en déduit que l'arrondi à l'unité de 14,569 est 15. De même, l'arrondi au dixième de 14,569 est 14,6.
On note 14,569 \approx 14,6 pour dire « 14,569 est environ égal à 14,6 ».
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
