Chapitre 7
Entrée en matière
Divisions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des mathsLes méthodes de division au cours des âges
Durant le Moyen Âge, en Europe, on utilisait une technique
de division nommée « division par facteurs ».
La méthode est la suivante : pour diviser par 12, on fait
une première division par 6 puis une seconde division par 2.
Cela facilite les divisions, puisqu'on manipule moins de
grands nombres. Autre exemple : puisque 36 = 9 × 4,
900 ÷ 36 est égal à (900 ÷ 9) ÷ 4 = 100 ÷ 4 = 25.
Cette méthode demande de connaître parfaitement les tables de multiplication ! Plus tard se développe la « division en galère » qui est une méthode de division posée. Elle a été très utilisée en Europe jusqu'à être finalement remplacée par la « méthode de la potence », plus courte, qui est utilisée encore aujourd'hui.
Cette méthode demande de connaître parfaitement les tables de multiplication ! Plus tard se développe la « division en galère » qui est une méthode de division posée. Elle a été très utilisée en Europe jusqu'à être finalement remplacée par la « méthode de la potence », plus courte, qui est utilisée encore aujourd'hui.

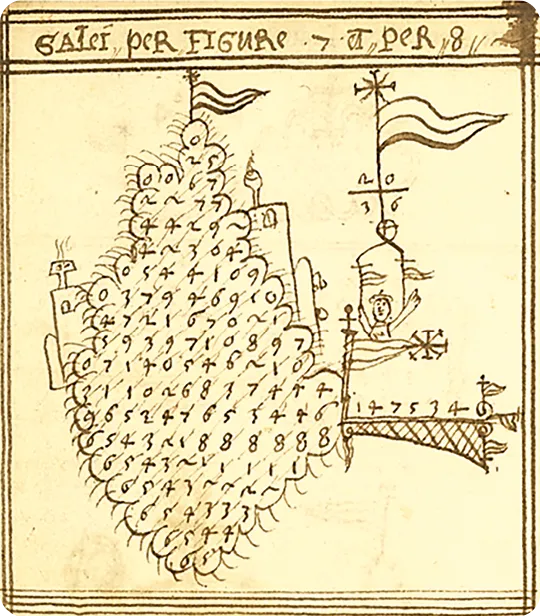
S. Lauretij, Travail arithmétique, XVIe siècle, université Columbia.
En utilisant la méthode de division par facteurs, calculer 300 ÷ 12.
Supplément numérique
Retrouvez cette histoire en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les maths, à quoi ça sert ?
En mathématique, l'opération « modulo » correspond au reste de la
division euclidienne de deux nombres entiers.
Par exemple, 42 modulo 5 égale 2 car 42 = 8 × 5 + 2.
Dans la vie courante, le modulo est utilisé de manière inconsciente lors de la manipulation des heures sur une pendule. En effet, cette dernière fonctionne modulo 12 : toutes les 12 heures, les aiguilles reprennent leur position initiale.
Par exemple, 18 = 1 × 12 + 6, donc 6 h et 18 h sont représentées de la même manière sur une pendule : la petite aiguille est sur le 6.
On peut également utiliser le modulo lorsqu'on parle des jours de la semaine. Dans ce cas, on utilise le modulo 7. Sans nous en rendre compte, nous utilisons les divisions euclidiennes dans ce contexte.
Par exemple, 42 modulo 5 égale 2 car 42 = 8 × 5 + 2.
Dans la vie courante, le modulo est utilisé de manière inconsciente lors de la manipulation des heures sur une pendule. En effet, cette dernière fonctionne modulo 12 : toutes les 12 heures, les aiguilles reprennent leur position initiale.
Par exemple, 18 = 1 × 12 + 6, donc 6 h et 18 h sont représentées de la même manière sur une pendule : la petite aiguille est sur le 6.
On peut également utiliser le modulo lorsqu'on parle des jours de la semaine. Dans ce cas, on utilise le modulo 7. Sans nous en rendre compte, nous utilisons les divisions euclidiennes dans ce contexte.


156 jours après un lundi, quel jour sommes-nous ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationComprendre les critères de divisibilité
Pour réaliser cette activité, utiliser la .
1. Combien y a-t-il de croix sur la carte ?
2. a. Est-il possible de regrouper ces croix par paquets de 2 sans qu'il ne reste de croix non
groupées ? Combien obtient-on de paquets ?
b. Écrire le nombre de croix en complétant l'égalité suivante :...=... × 2.
1. Combien y a-t-il de croix sur la carte ?
3. a. Est-il possible de regrouper ces croix par paquets de 5 sans qu'il ne reste de croix non
groupées ? Combien obtient-on de paquets complets ?
b. Écrire le nombre de croix en complétant l'égalité suivante :...=...~×~5~+....
4. Pourquoi peut-on affirmer que le nombre de croix n'est pas divisible par 10 ?
Bilan
Rappeler la méthode pour savoir si un nombre est divisible par 2, par 5 ou par 10.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Effectuer une division euclidienne
Hortense a commencé une vidéo où elle explique comment poser la division
euclidienne de 854 par 3.
1. Regarder attentivement la .
2. Poursuivre la méthode d'Hortense afin de terminer la division euclidienne.
3. Dans une division posée, où écrit-on le diviseur, le dividende, le quotient et le reste ?
Écrire la division euclidienne d'Hortense sous forme d'une égalité utilisant une multiplication. Préciser où se trouvent, dans cette égalité, le diviseur, le dividende, le quotient et le reste.
1. Regarder attentivement la .
2. Poursuivre la méthode d'Hortense afin de terminer la division euclidienne.
Bilan
Écrire la division euclidienne d'Hortense sous forme d'une égalité utilisant une multiplication. Préciser où se trouvent, dans cette égalité, le diviseur, le dividende, le quotient et le reste.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 2Comprendre le sens de la division décimale
On veut répartir équitablement 1,5~\mathrm{L} de jus d'orange dans
six verres.
On doit alors déterminer quel volume de jus d'orange il faut
verser dans chaque verre.
1.Convertir 1,5 litre en centilitre.
2. Écrire sous forme d'une égalité la division euclidienne
du volume obtenu en centilitre par 6. A quoi correspond
le quotient obtenu dans le contexte de l'exercice ?
3.
Convertir ce quotient en litre et écrire alors la division de 1,5 par 6 sous forme d'une égalité.
Que peut-on conclure par rapport au problème initial ?


Bilan
Comment faire pour répartir équitablement 2,45~\mathrm{L} de jus d'orange dans sept verres ? Que se passe-t-il si on souhaite répartir équitablement 1,9~\mathrm{L} dans six verres ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

