Chapitre 7
Cours
Divisions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Division euclidienne
Définitions
On se donne deux nombres entiers a et b ≠ 0. On dit que a est divisible par b lorsqu'il existe un nombre entier q tel que a = b × q. On appelle le nombre q le quotient de la division de a par b. On dit alors que a est un multiple de b et que b est un diviseur de a.
Exemple :
56 = 7 × 8 donc 56 est divisible par 7 ; 56 est un multiple de 7 et 7 est un diviseur de 56.
On peut aussi dire que 56 est divisible par 8 ; 56 est un multiple de 8 et 8 est un diviseur de 56.
On peut aussi dire que 56 est divisible par 8 ; 56 est un multiple de 8 et 8 est un diviseur de 56.
Propriétés : critères de divisibilité
Un nombre entier est divisible par :
- 2 si, et seulement si, son chiffre des unités est 0, 2, 4, 6 ou 8 ;
- 5 si, et seulement si, son chiffre des unités est 0 ou 5 ;
- 10 si, et seulement si, son chiffre des unités est 0.
Exemples :
1. 76 : le chiffre des unités de 76 est 6 donc 76 est divisible par 2, mais pas par 5 ni par 10.
2. 25 : le chiffre des unités de 25 est 5 donc 25 est divisible par 5, mais pas par 2 ni par 10.
3. 80 : le chiffre des unités de 80 est 0 donc 80 est divisible par 2, 5 et 10.
2. 25 : le chiffre des unités de 25 est 5 donc 25 est divisible par 5, mais pas par 2 ni par 10.
3. 80 : le chiffre des unités de 80 est 0 donc 80 est divisible par 2, 5 et 10.
Définitions
Effectuer la division euclidienne d'un nombre entier (le dividende) par un nombre entier différent de 0 (le diviseur), c'est déterminer les deux uniques nombres entiers, le quotient et le reste, tels que dividende = diviseur \times quotient + reste, où le reste doit être strictement inférieur au diviseur.
Exemple :

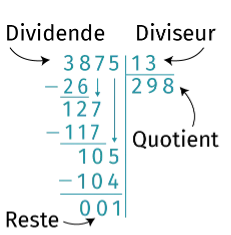
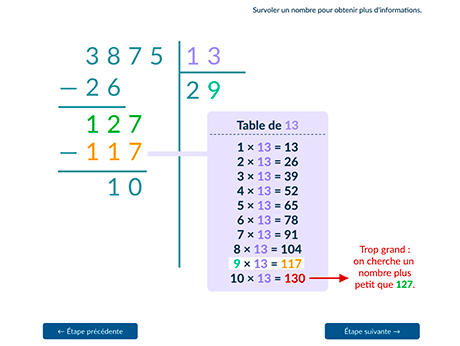
Grâce à la division posée suivante, on peut écrire la
division euclidienne 3\;875 = 13 × 298 + 1.
La division euclidienne de 3\;875 par 13 a pour quotient 298 et pour reste 1 (on a bien 1 < 13).
La division euclidienne de 3\;875 par 13 a pour quotient 298 et pour reste 1 (on a bien 1 < 13).

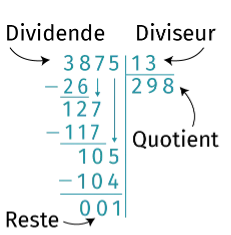
- Remarque :
On peut se servir de la division euclidienne pour trouver l'écriture de \frac{3\;875}{13} sous forme d'un nombre mixte.
\frac{3\;875}{13} = \frac{298 × 13 + 1}{13} = \frac{298 × 13}{13} + \frac{1}{13} = 298 + \frac{1}{13}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Division décimale
Définitions
Effectuer la division décimale d'un nombre décimal (le dividende) par un nombre entier différent de 0 (le diviseur), c'est effectuer l'algorithme qui détermine, lorsqu'il s'arrête, l'unique nombre (le quotient décimal) tel que : dividende = diviseur \times quotient décimal.
Lorsque l'algorithme ne s'arrête pas, la division décimale permet de déterminer une valeur approchée du quotient à n'importe quel rang.
Propriété
Lorsque l'algorithme de la division décimale de deux nombres entiers a par b s'arrête, la fraction \frac{a}{b} est un nombre décimal.
Exemples :
1. 4,5 = 3 \times 1,5 donc le quotient décimal de 4,5 par 3 est 1,5.

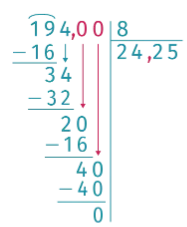
3. Quand on obtient un reste qu'on avait déjà obtenu, cela signifie que les opérations vont toujours être les mêmes et que les restes vont se répéter. La division ne se terminera jamais : il est donc inutile de continuer.


Cette division ne se termine jamais, le quotient de 166 par 3 a une infinité de chiffres après la virgule : ce n'est pas un nombre décimal. La fraction \frac{166}{3} n'est donc pas un nombre décimal.
On peut dire en revanche que 166 \div 3 \approx 55. Le nombre 55 est une valeur approchée à l'unité du quotient de 166 par 3.
1. 4,5 = 3 \times 1,5 donc le quotient décimal de 4,5 par 3 est 1,5.
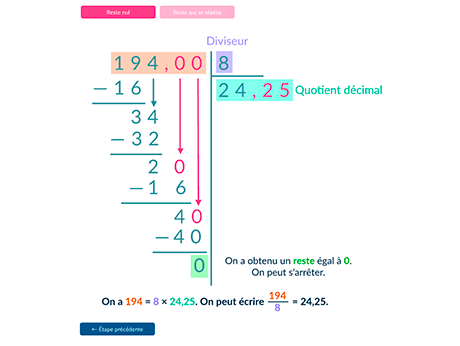
2. Il peut être nécessaire de rajouter des 0 dans la partie
décimale de l'écriture du dividende afin de pouvoir
terminer la division. Ici, l'algorithme de la division
décimale de 194 par 8 s'arrête.
194 = 8 \times 24,25 donc la fraction \frac{194}{8} est un nombre décimal : \frac{194}{8} = 24,25.
194 = 8 \times 24,25 donc la fraction \frac{194}{8} est un nombre décimal : \frac{194}{8} = 24,25.

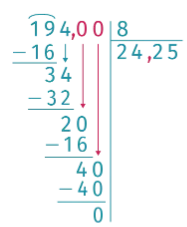
3. Quand on obtient un reste qu'on avait déjà obtenu, cela signifie que les opérations vont toujours être les mêmes et que les restes vont se répéter. La division ne se terminera jamais : il est donc inutile de continuer.


Cette division ne se termine jamais, le quotient de 166 par 3 a une infinité de chiffres après la virgule : ce n'est pas un nombre décimal. La fraction \frac{166}{3} n'est donc pas un nombre décimal.
On peut dire en revanche que 166 \div 3 \approx 55. Le nombre 55 est une valeur approchée à l'unité du quotient de 166 par 3.
- Remarque : Pour obtenir l'arrondi du quotient à un rang donné, il faut faire le calcul jusqu'au rang suivant.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille