Chapitre 12
Entrée en matière
Droites et segments
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des mathsLa géométrie d'Euclide
L'ouvrage de mathématiques le plus connu
est sans nul doute celui du mathématicien
grec Euclide. Intitulé Éléments et écrit environ
300 ans avant notre ère, c'est l'ouvrage
scientifique le plus édité de l'Histoire !
Dans cet ouvrage, Euclide pose les bases de la géométrie. Le point est le premier objet mathématique à être défini et, à partir de lui, sont définis la droite, puis les parallèles, puis le cercle, etc.
En plus de ces définitions, il propose cinq axiomes (ou postulats), c'est-à-dire des énoncés qu'il considère comme vrais et qu'il demande d'admettre. De cette petite base, il construit alors l'ensemble de la géométrie en démontrant toutes les propriétés de son ouvrage.
Dans cet ouvrage, Euclide pose les bases de la géométrie. Le point est le premier objet mathématique à être défini et, à partir de lui, sont définis la droite, puis les parallèles, puis le cercle, etc.
En plus de ces définitions, il propose cinq axiomes (ou postulats), c'est-à-dire des énoncés qu'il considère comme vrais et qu'il demande d'admettre. De cette petite base, il construit alors l'ensemble de la géométrie en démontrant toutes les propriétés de son ouvrage.


Ishaq ibn Hunayn, Éléments d'Euclide traduit en arabe, IXᵉ siècle, Bibliothèque Chester-Beatty.
Faire des recherches et retrouver les cinq postulats d'Euclide.
Supplément numérique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les maths, à quoi ça sert ?
Pour se repérer sur la Terre,
en particulier pour les
avions et les bateaux, une
méthode consiste à découper
le globe selon plusieurs droites
« verticales » qui vont du pôle Nord au pôle
Sud et d'autres droites « horizontales » qui
sont parallèles à l'équateur. Sur une carte
plane, ces droites se retrouvent parallèles
les unes aux autres.

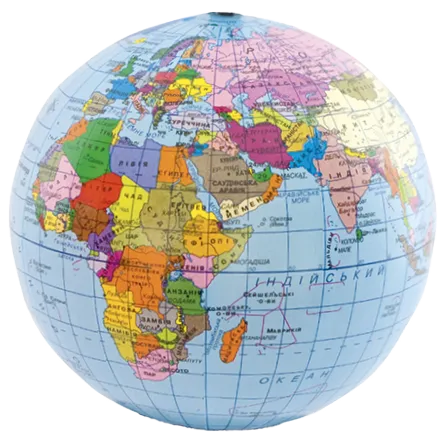

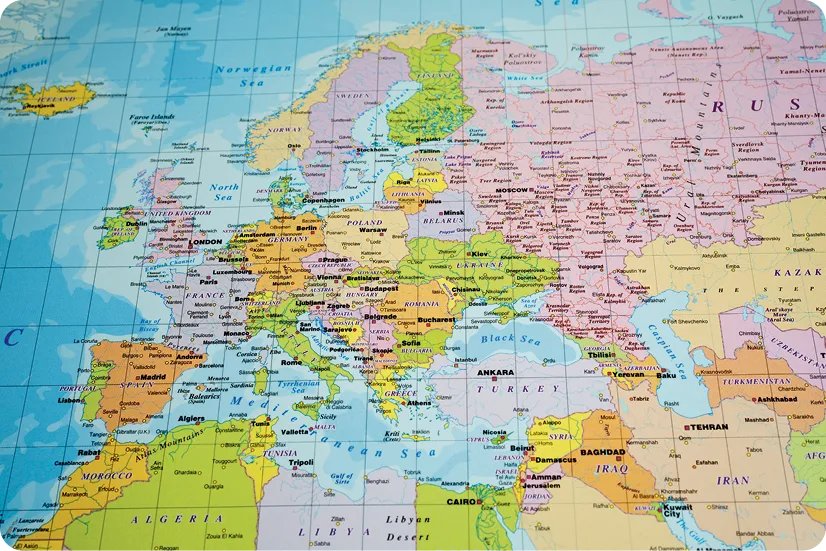




Les droites qui vont du pôle Nord au pôle Sud sont-elles vraiment parallèles ?
Supplément numérique
Visualisez ces .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Découvrir les symboles ∈ et ∉
Cliquez pour accéder à GeoGebra
1. Ouvrez le module Geogebra ou la figure.
2. À l'aide d'une règle, tracer précisément le trait qui part du point \text {A} et qui va jusqu'au point \text {B}.
Comment s'appelle ce trait : le segment \text {[AB]} ou la droite \text {(AB)} ?
3. On constate que le point \text {K} est sur le trait
tracé. On dit que \text {K} appartient à \text {[AB]} et on note
\mathrm{K} \in[\mathrm{AB}]. Justifier les propositions suivantes.
a. \mathrm{H} \in[\mathrm{AB}] b. \mathrm{G} \notin[\mathrm{AB}] c. \mathrm{I} \notin[\mathrm{AB}]
4.
On prolonge \text {[AB]} de part et d'autre des points \mathrm{A} et \mathrm{B} pour obtenir la droite \text {(AB)}. Compléter
les propositions suivantes avec ∈ ou ∉.
Comment s'appelle ce trait : le segment \text {[AB]} ou la droite \text {(AB)} ?
a. \mathrm{H} \in[\mathrm{AB}]
a. \text {I} \text {(AB)}
b. \text {L} \text {(AB)}
c. \text {H} \text {(AB)}
5. Tracer la droite \text {(CD)} et compléter les propositions suivantes avec ∈ ou ∉.
6. Pourquoi dit-on que \text {K} est le point d'intersection des droites \text {(AB)} et \text {(CD)} ?
Pour deux points distincts \text {A} et \text {B}, est-il possible de placer un point \text {C} tel que \mathbf{C} \in[\mathbf{A B}] et \mathbf{C} \notin(\mathbf{A B}) ? Et de placer un point \text {D} tel que \mathbf{D} \in(\mathbf{A B}) et \mathbf{D} \notin[\mathbf{A B}] ? Justifier.
a. \text {E} \text {[CD]}
b. \text {F} \text {(CD)}
c. \text {J} \text {(CD)}
d. \text {M} \text {[CD]}
b. \text {F} \text {(CD)}
c. \text {J} \text {(CD)}
d. \text {M} \text {[CD]}
e. \text {E} \text {(CD)}
f. \text {F} \text {[CD]}
g. \text {J} \text {[CD]}
h. \text {M} \text {(CD)}
f. \text {F} \text {[CD]}
g. \text {J} \text {[CD]}
h. \text {M} \text {(CD)}
Bilan
Pour deux points distincts \text {A} et \text {B}, est-il possible de placer un point \text {C} tel que \mathbf{C} \in[\mathbf{A B}] et \mathbf{C} \notin(\mathbf{A B}) ? Et de placer un point \text {D} tel que \mathbf{D} \in(\mathbf{A B}) et \mathbf{D} \notin[\mathbf{A B}] ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationÉtablir un lien entre longueur et appartenance
Prévoir trois cure-dents par binôme et un morceau de carton.
1. Reproduire plusieurs fois les étapes suivantes.
2. Existe-t-il des cas pour lesquels \mathrm{AB}+\mathrm{BC}=\mathrm{AC} ?
1. Reproduire plusieurs fois les étapes suivantes.
- Planter les trois cure-dents dans le carton.
- Chaque emplacement de cure-dents représente respectivement les points \text {A}, \text {B} et \text {C}.
- Mesurer la longueur \text {AB} et la longueur \text {BC}.
- Calculer \mathrm{AB}+\mathrm{BC}.
- Mesurer la longueur \text {AC}.
- Comparer \mathrm{AB}+\mathrm{BC} et \text {AC}.


Bilan
Pour trois points \mathrm{A}, \mathrm{B} et \mathrm{C}, que peut-on dire de la longueur \mathrm{AC} en comparaison avec la somme \mathrm{AB + BC} ? Quel est le plus court chemin de \mathrm{A} jusqu'à \mathrm{C} ?
Version interactive
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


