Chapitre 12
Cours
Droites et segments
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Premiers éléments de géométrie
Définition
Un point est le plus petit élément du plan : il n'a ni longueur ni largeur. Il est représenté par une croix.
En général, on note les points à l'aide de lettres majuscules : \mathrm{A}, \mathrm{B}, \mathrm{C}, etc.
Propriété
Par deux points distincts, il passe une unique droite.

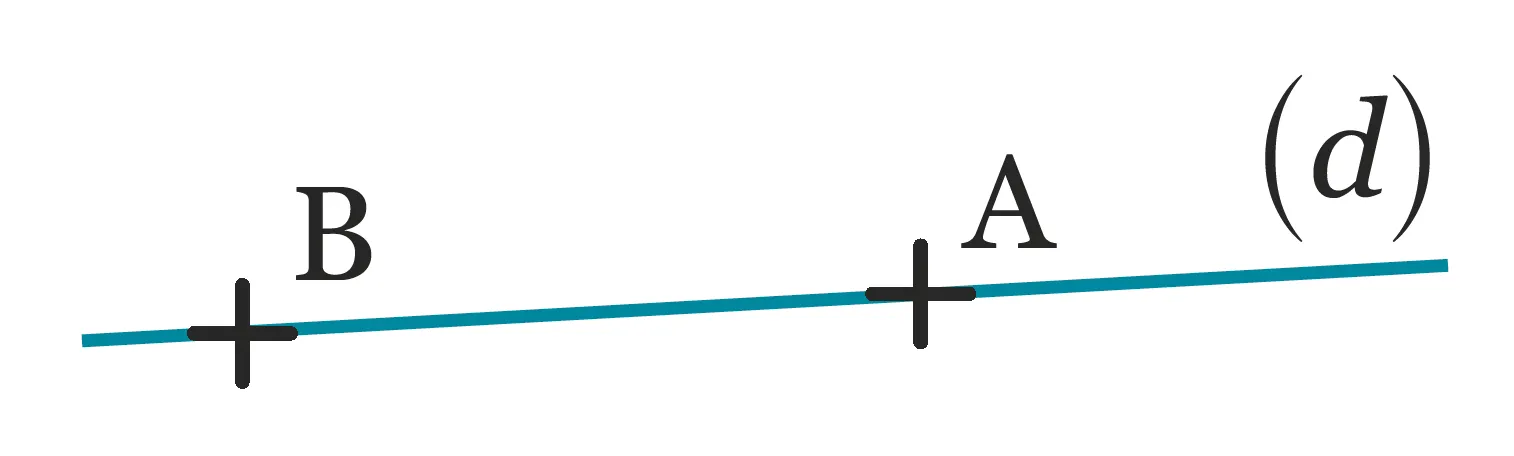
Notation : La droite qui passe par les points \mathrm{A} et \mathrm{B} est nommée en utilisant le nom de ces deux points entre parenthèses. On écrit : la droite \mathrm{(AB)} ou la droite \mathrm{(BA)}.
- Remarques : (d) est un autre nom de la droite \mathrm{(AB)} ci-dessus.
- Une droite est composée d'une infinité de points.
- On peut prolonger la droite \mathrm{(AB)} aussi loin que l'on veut au-delà de \mathrm{A} et de \mathrm{B}.
Définition
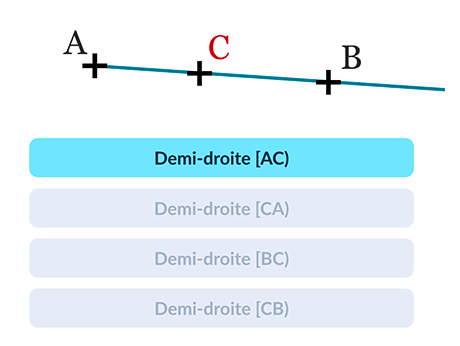
Lorsque l'on place un point \mathrm{C} sur une droite \mathrm{(AB)}, on définit deux demi-droites d'origine \mathrm{C}. Les points \mathrm{A}, \mathrm{B} et \mathrm{C} sont dits alignés.
Notation : On note \mathrm{[CB)} la demi-droite représentée en rouge
d'origine \mathrm{C} passant par le point \mathrm{B}. On note \mathrm{[CA)} la demi-droite représentée en bleu d'origine \mathrm{C} passant par \mathrm{A}.


Version interactive
Définition
Lorsqu'un point \mathrm{A} appartient à la droite (d), on note \mathrm{A} ∈ (d).
Dans le cas contraire, on dit que \mathrm{A} n'appartient pas à la droite (d) et on note \mathrm{A} ∉ (d).
Exemple :

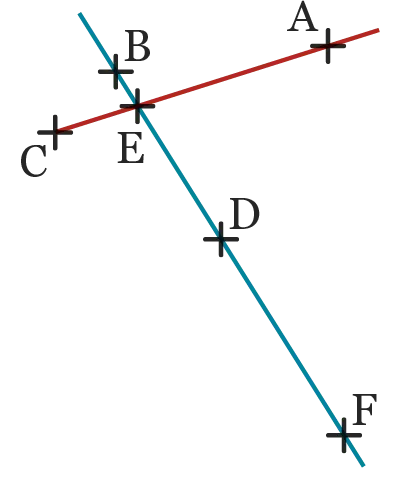
Sur la figure suivante, il y a six points : \mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E} et \mathrm{F}.
La droite \mathrm{(BD)} a d'autres noms : \mathrm{(EF)} ou encore \mathrm{(DE)}.
\mathrm{E} est le point d'intersection de la droite \mathrm{(CA)} et de la droite \mathrm{(BF)}. Les droites \mathrm{(CA)} et (\mathrm{BF)} sont sécantes en \mathrm{E}.
Le point \mathrm{D} appartient à la droite \mathrm{(BF)}. On note \mathrm{D∈(BF)}.
Le point \mathrm{B} n'appartient pas à la demi-droite \mathrm{[EF)}. On note \mathrm{B∉ [EF)}.
Le point \mathrm{A} n'appartient pas à la droite \mathrm{(CD)}. On note \mathrm{A ∉ (CD)}.
Autrement dit, les points \mathrm{A}, \mathrm{C} et \mathrm{D} ne sont pas alignés.
La droite \mathrm{(BD)} a d'autres noms : \mathrm{(EF)} ou encore \mathrm{(DE)}.
\mathrm{E} est le point d'intersection de la droite \mathrm{(CA)} et de la droite \mathrm{(BF)}. Les droites \mathrm{(CA)} et (\mathrm{BF)} sont sécantes en \mathrm{E}.
Le point \mathrm{D} appartient à la droite \mathrm{(BF)}. On note \mathrm{D∈(BF)}.
Le point \mathrm{B} n'appartient pas à la demi-droite \mathrm{[EF)}. On note \mathrm{B∉ [EF)}.
Le point \mathrm{A} n'appartient pas à la droite \mathrm{(CD)}. On note \mathrm{A ∉ (CD)}.
Autrement dit, les points \mathrm{A}, \mathrm{C} et \mathrm{D} ne sont pas alignés.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Segment et longueur
Définition
Un segment est une partie de droite délimitée par deux points, appelés extrémités du segment.

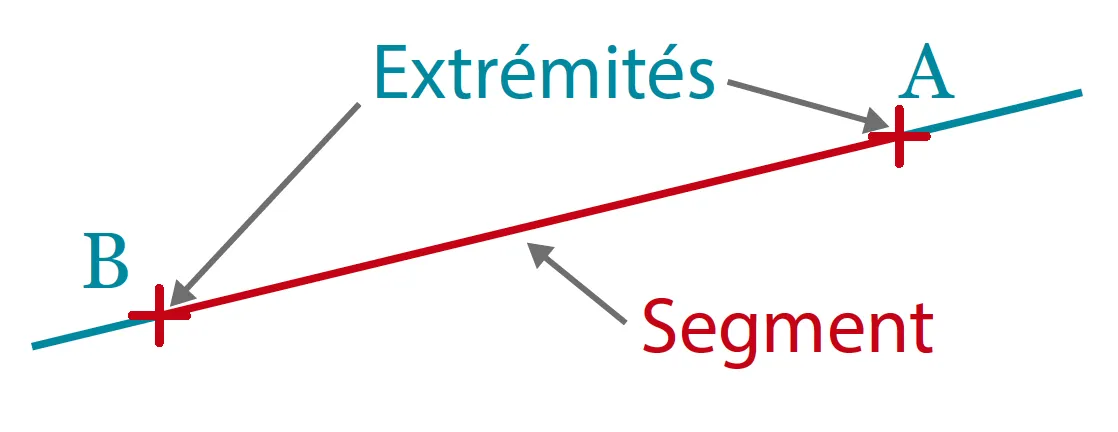
Notation : Le segment de droite d'extrémités \mathrm{A} et \mathrm{B} est nommé en utilisant le nom de ces points entre crochets. On écrit : le segment \mathrm{[AB]}. Il ne faut donc pas confondre le segment \mathrm{[AB]} avec la droite \mathrm{(AB)} et la demi-droite \mathrm{[AB)}.
Propriété
Le segment \mathrm{[AB]} est le plus court chemin pour aller du point \mathrm{A} au point \mathrm{B}.
Définition
La distance entre deux points \mathrm{A} et \mathrm{B} est la longueur du segment \mathrm{[AB]}. Cette longueur est notée \mathrm{AB}.
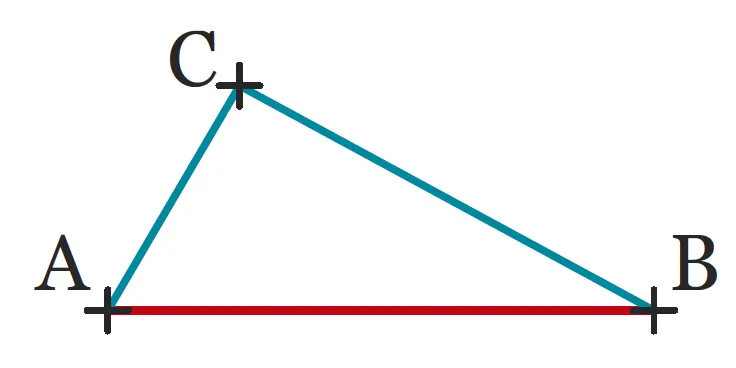
Propriété (inégalité triangulaire)
Pour tous points \mathrm{A}, \mathrm{B} et \mathrm{C}, \mathrm{A C+B C \geqslant A B}.
De plus, \mathrm{AC+CB = AB} si, et seulement si, \mathrm{C∈ [AB]}.

Définition
Le milieu d'un segment est le point qui appartient à ce
segment et qui est à égale distance des extrémités de ce
segment.


Exemple :
Sur la figure ci-dessus, le point \mathrm{J} est équidistant (à égale distance) de \mathrm{S} et de \mathrm{T} et il appartient au segment \mathrm{[ST]} : \mathrm{J} est donc le milieu de \mathrm{[ST]}.
Sur la figure ci-dessus, le point \mathrm{J} est équidistant (à égale distance) de \mathrm{S} et de \mathrm{T} et il appartient au segment \mathrm{[ST]} : \mathrm{J} est donc le milieu de \mathrm{[ST]}.
- Remarque : Une droite est illimitée : elle n'a ni longueur ni milieu.
Définition
Le périmètre d'un polygone est la somme des longueurs de ses côtés.
Exemple :
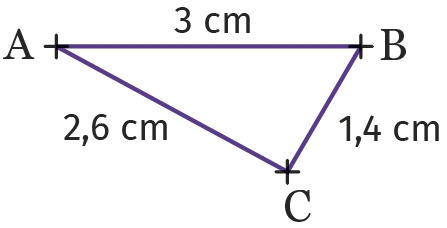
Le périmètre du triangle \mathrm{ABC} est
Le périmètre du triangle \mathrm{ABC} est
\mathrm{AB}+\mathrm{BC}+\mathrm{AC}=3 \mathrm{~cm}+2,6 \mathrm{~cm}+1,4 \mathrm{~cm}=7 \mathrm{~cm}.

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille