Chapitre 15
Entrée en matière
Symétrie axiale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des mathsLe problème de Héron d'Alexandrie
Les Grecs sont parmi les premiers à avoir étudié
les propriétés de la symétrie. Au Ier siècle, par
exemple, le mathématicien Héron d'Alexandrie
propose un problème dont la solution utilise la
symétrie axiale. Ce problème est le suivant : sur
la figure suivante, quel est le plus court chemin
reliant \text {A} à \text {B} en passant une fois par la droite (d) ?
Autrement dit, où doit-on placer le point \text {C} sur la droite (d) pour que \mathrm{AC}+\mathrm{CB} soit
minimale ? Pour résoudre ce problème, Héron construit B^{\prime}, le symétrique de \text {B} par
rapport à (d) et remarque que
\mathrm{AC}+\mathrm{CB}=\mathrm{AC}+\mathrm{CB^{\prime}}. Le plus court chemin entre \text {A} et est la ligne droite, ce qui permet de savoir où placer le point \text {C}.
\mathrm{AC}+\mathrm{CB}=\mathrm{AC}+\mathrm{CB^{\prime}}. Le plus court chemin entre \text {A} et est la ligne droite, ce qui permet de savoir où placer le point \text {C}.

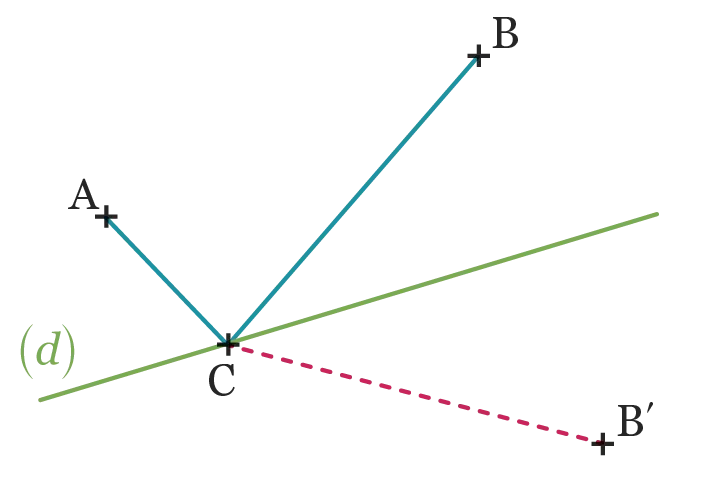
Reproduire la situation et construire la solution au problème.
Supplément numérique
Retrouvez cette histoire en .
Cliquez pour accéder à GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les maths, à quoi ça sert ?
Sur les véhicules d'urgence (ambulance, camion
de pompier, voiture de police, etc.), on peut
constater que les mots à l'avant de la voiture
sont écrits à l'envers. Pourquoi ? La symétrie
axiale permet de répondre à cette question. En
voiture, lorsque l'on aperçoit une ambulance
dans son rétroviseur, le mot apparaît alors
à l'endroit. C'est l'effet miroir de la symétrie
axiale.


Comment écrire le mot AMBULANCE sur le capot d'une voiture pour
qu'il soit correctement lisible en regardant dans un rétroviseur ?
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Déterminer une propriété caractéristique de la médiatrice
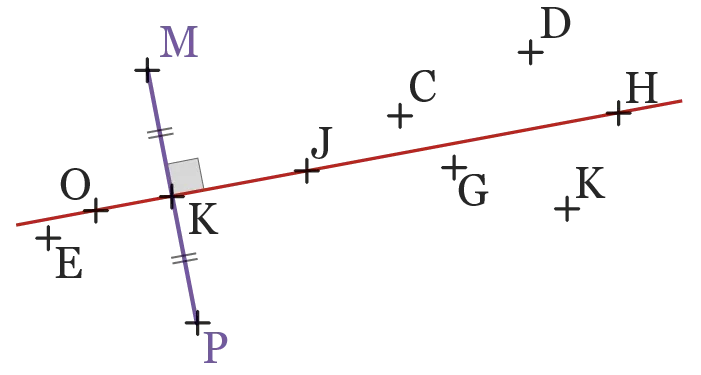
On a tracé en rouge la médiatrice du segment [\mathrm{MP}].

1.
Observer la figure et, en mesurant à l'aide
d'une règle, donner :
a. les points plus proches de \text {M} que de \text {P} ;
b. les points à égale distance de \text {M} et de \text {P} ;
c. les points plus proches de \text {P} que de \text {M}.
2. Je souhaite placer un nouveau point situé à égale
distance de \text {M} et \text {P} : où dois-je le placer?
a. les points plus proches de \text {M} que de \text {P} ;
Bilan
Que peut-on conclure à propos des points situés sur la médiatrice d'un segment ? Et qu'en est-il de ceux qui n'y sont pas situés ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationDéterminer l'axe de symétrie d'un segment
1.
Sur un petit morceau de papier blanc, tracer un segment \text {[AB]} de longueur 8 \mathrm{~cm}.
2. Plier la feuille de telle sorte que \text {A} et \text {B} soient superposés. Marquer le pli.
3. Déplier la feuille et tracer la droite (d) qui est le long de cette pliure. Noter \text{I} son point d'intersection avec le segment \text {[AB]}.
2. Plier la feuille de telle sorte que \text {A} et \text {B} soient superposés. Marquer le pli.
3. Déplier la feuille et tracer la droite (d) qui est le long de cette pliure. Noter \text{I} son point d'intersection avec le segment \text {[AB]}.
4. a. Que peut-on dire de \text{I} par rapport à \text {[AB]} ?
b. Que peut-on dire de la droite (d) et du segment \text {[AB]} ?
Bilan
Pourquoi peut-on dire que les points \mathrm{A} et \mathrm{B} sont symétriques par rapport à (d) ? On appelle cette droite la médiatrice du segment [\mathrm{AB}]. Quelles sont ses caractéristiques ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité de manipulationDécouvrir les propriétés de la symétrie
Pour réaliser cette activité, utiliser la .
Comment les distances et les angles se comportent-ils lorsque l'on applique une symétrie axiale à une figure ?
1. Sur une feuille au format A5, réaliser le pliage indiqué sur la figure 1 de la fiche.
2. Que représente l'axe en rouge de l'étape 1 pour l'avion ?
3. Déplier l'avion pour le remettre au niveau de l'étape 5, puis nommer les points comme sur la figure 2.
2. Que représente l'axe en rouge de l'étape 1 pour l'avion ?
4. Mesurer les distances \text {OA}, \text {OB}, \text {OC} et \text {OD}. Y a-t-il des distances égales ?
5. Mesurer les angles \widehat{\mathrm{AOB}} et \widehat{\mathrm{COD}}. Que peut-on remarquer ?
Bilan
Comment les distances et les angles se comportent-ils lorsque l'on applique une symétrie axiale à une figure ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

