Chapitre 15
Cours
Symétrie axiale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Médiatrice d'un segment
Définition
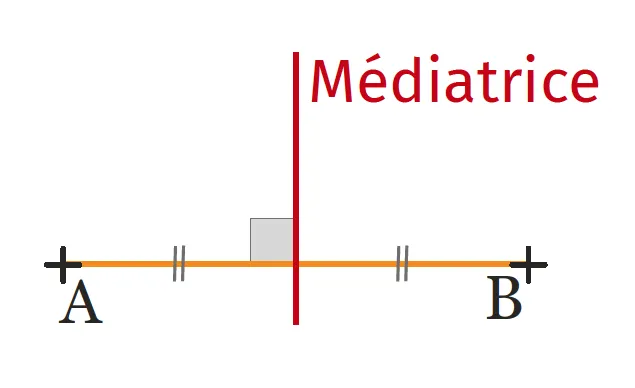
La médiatrice d'un segment est la droite qui est perpendiculaire à
ce segment et qui passe par son milieu.

Propriétés
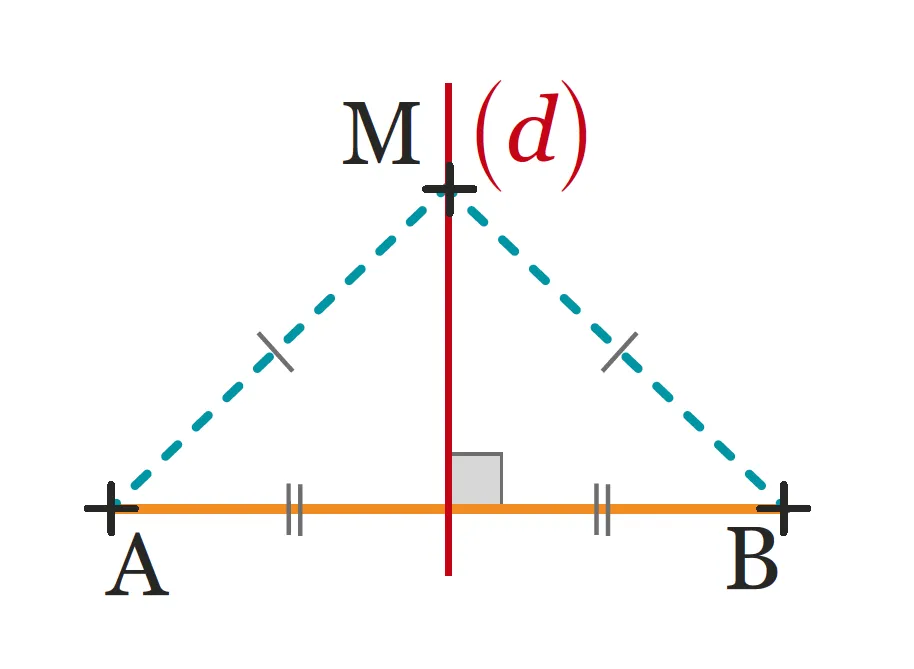
1. Si un point \text {M} appartient à la médiatrice (d) d'un segment [\mathrm{AB}],
alors il est équidistant (à égale distance) de ses extrémités.
Autrement dit, si \text {M} \in(d) alors \mathrm{MA} = \mathrm{MB}.
2. Si un point n'appartient pas à la médiatrice d'un segment, alors il est plus proche de l'une des extrémités que de l'autre.
Autrement dit, si \text {M} \in(d) alors \mathrm{MA} = \mathrm{MB}.
2. Si un point n'appartient pas à la médiatrice d'un segment, alors il est plus proche de l'une des extrémités que de l'autre.

Exemple :

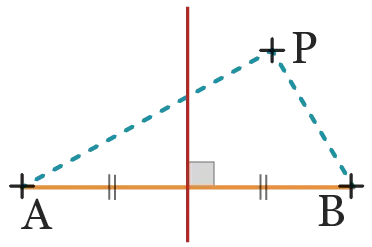
Le point \text {P} n'appartient pas à la médiatrice de [\mathrm{AB}] : il est
plus proche de \text {B} que de \text {A}.


Version interactive
Propriété
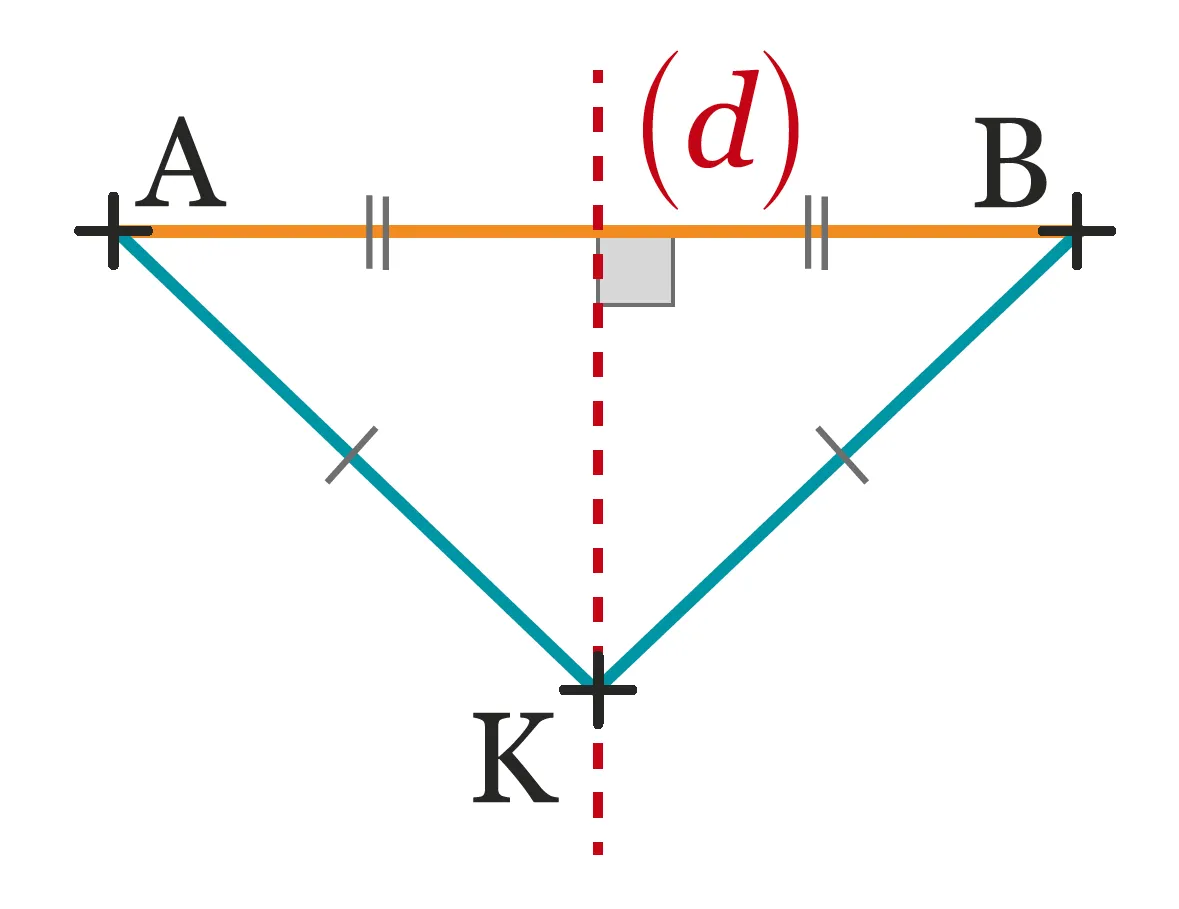
Si un point \text {K} est situé à égale distance de deux points \text {A} et \text {B}, alors
il appartient à la médiatrice (d) du segment [\mathrm{AB}].
Autrement dit, si \mathrm{KA} = \mathrm{KB} alors \mathrm{K} \in(d).
Autrement dit, si \mathrm{KA} = \mathrm{KB} alors \mathrm{K} \in(d).

Propriété caractéristique de la médiatrice
La médiatrice d'un segment est l'ensemble des points équidistants des extrémités de ce segment.
Exemple :

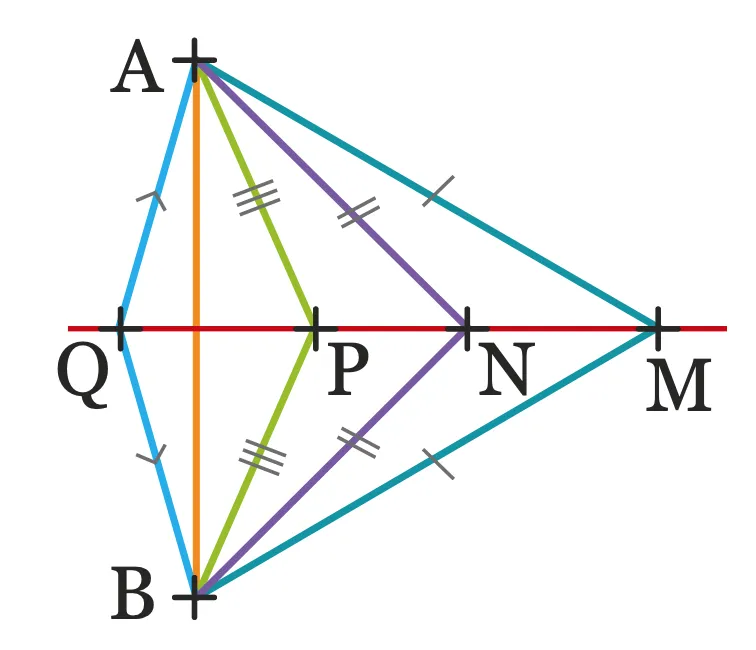
D'après le codage, \text {M}, \text {N}, \text {P} et \text {Q} sont à égale distance de
\text {A} et de \text {B} donc ils appartiennent tous à la médiatrice de
\text {[AB]}, tracés ici en rouge.


- Remarque :
Il est possible de construire la médiatrice d'un segment uniquement à l'aide d'un compas et d'une règle non graduée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Symétrie axiale
Définitions
Deux points \text {A} et \text {B} sont symétriques par rapport à une droite (d) lorsque (d) est la médiatrice du segment [\mathrm{AB}]. Cette symétrie qui transforme \text {A} en \text {B} est appelée symétrie axiale d'axe (d).
Exemple :
La droite (d) passe par le milieu \text {M} de [\mathrm{AB}] et est perpendiculaire à (\text{AB}) : la droite (d) est donc la médiatrice du segment [\mathrm{AB}].
On en déduit que le symétrique du point \text{A} par rapport à la droite (d) est le point \text{B}.
Par ailleurs, la droite (d) passe par le milieu \text {P} de [\mathrm{AC}] mais n'est pas perpendiculaire à [\mathrm{AB}] : la droite (d) n'est donc pas la médiatrice de [\mathrm{AC}].
La droite (d) passe par le milieu \text {M} de [\mathrm{AB}] et est perpendiculaire à (\text{AB}) : la droite (d) est donc la médiatrice du segment [\mathrm{AB}].
On en déduit que le symétrique du point \text{A} par rapport à la droite (d) est le point \text{B}.
Par ailleurs, la droite (d) passe par le milieu \text {P} de [\mathrm{AC}] mais n'est pas perpendiculaire à [\mathrm{AB}] : la droite (d) n'est donc pas la médiatrice de [\mathrm{AC}].
- Remarque : Si un point appartient à la droite (d), alors il est son propre symétrique par rapport à (d).
Propriété
La médiatrice d'un segment est l'axe de symétrie de ce segment.
Propriétés
Soit \text {A}, \text {B} et \text {C} trois points ayant respectivement pour symétriques par rapport à une droite (d) les points \text {A'}, \text {B'} et \text {C'}.
1. Le symétrique du segment [\mathrm{AB}] est le segment [\mathrm{A'B'}] et \mathrm{AB} = \mathrm{A'B'}.
2. Le symétrique de l'angle \widehat{\mathrm{ABC}} est l'angle \widehat{\mathrm{A'B'C'}} et \widehat{\mathrm{ABC}} = \widehat{\mathrm{A'B'C'}}.
3. Si \text {A}, \text {B} et \text {C} sont alignés alors \text {A'}, \text {B'} et \text {C'} sont aussi alignés dans le même ordre.
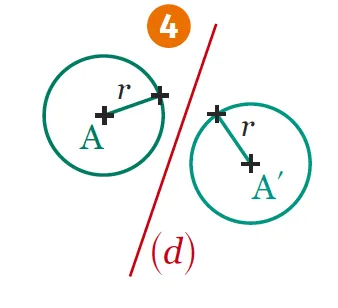
4. Le symétrique d'un cercle de centre \text {A} est le cercle de centre \text {A'} et de même rayon.

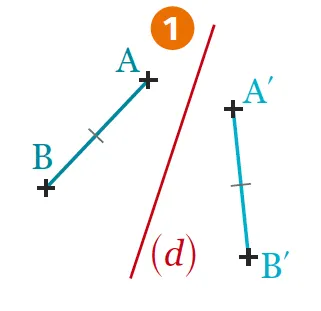
1

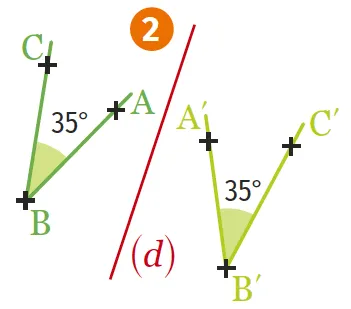
2

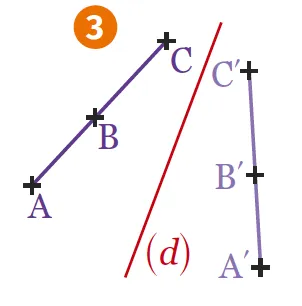
3

4
Propriété
La bissectrice d'un angle est l'axe de symétrie de cet angle.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

