Chapitre 17
Cours
Aires et volumes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Les aires
Définition
L'aire d'une figure plane est la mesure de sa surface dans une unité d'aire choisie.
Définition
- Le mètre carré est l'unité d'aire qui correspond à l'aire d'un carré de côté 1~\mathrm{m}.
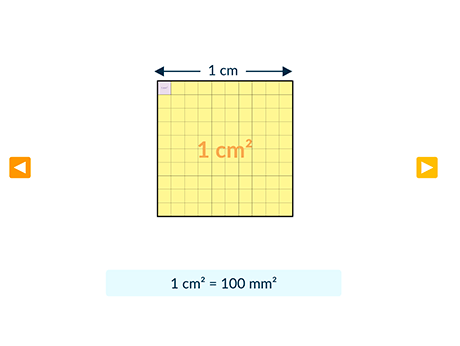
Son symbole est : \mathrm{m}^2. - Le centimètre carré est l'unité d'aire qui correspond à l'aire d'un carré de côté 1~\mathrm{cm}.
Son symbole est : \mathrm{cm}^2. - Le kilomètre carré est l'unité d'aire qui correspond à l'aire d'un carré de côté 1~\mathrm{km}.
Son symbole est : \mathrm{km}^2. - Le millimètre carré est l'unité d'aire qui correspond à l'aire d'un carré de côté 1~\mathrm{mm}.
Son symbole est : \mathrm{mm}^2.
Conséquence : Un carré de côté 1~\mathrm{m} a une aire de 1~\mathrm{m}^2.
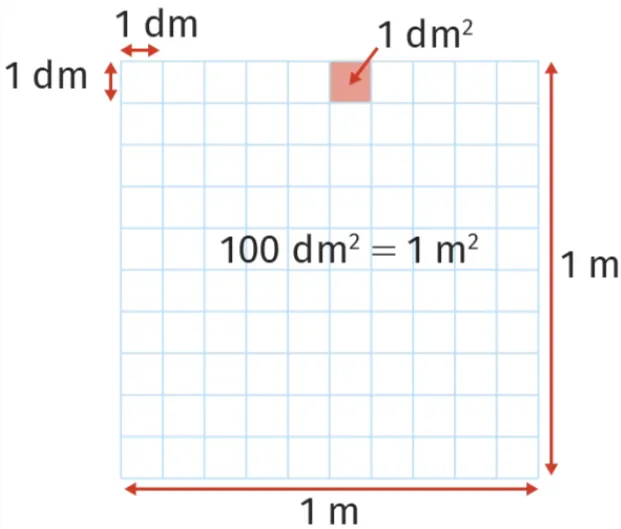
Or, on sait que 1~\mathrm{m} = 10~\mathrm{dm}. L'aire d'un carré de côté
10~\mathrm{dm} est : 10~\mathrm{dm} \times 10~\mathrm{dm} =100~\mathrm{dm}^2.
On peut donc dire que 1~\mathrm{m}^2 = 100~\mathrm{dm}^2.
Exemple :
On souhaite convertir 3,7~\mathrm{cm}^2 en \mathrm{dm}^2.
On sait que 1~\mathrm{cm} = 0,1~\mathrm{dm}, donc
On souhaite convertir 3,7~\mathrm{cm}^2 en \mathrm{dm}^2.
On sait que 1~\mathrm{cm} = 0,1~\mathrm{dm}, donc
1~\mathrm{cm}^2=1~\mathrm{cm} \times 1~\mathrm{cm} = 0,1~\mathrm{dm} \times 0,1~\mathrm{dm} = 0,01~\mathrm{dm}^2.
Par conséquent, 3,7~\mathrm{cm}^2 = 3,7 \times 0,01~\mathrm{dm}^2 = 0,037~\mathrm{dm}^2.

Version interactive
Propriété
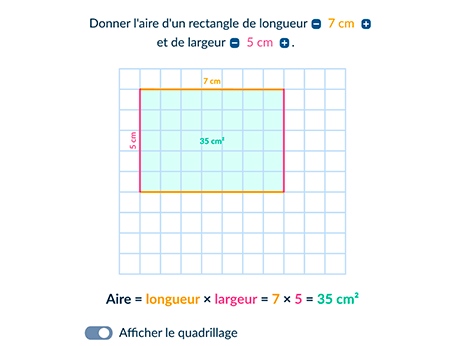
L'aire d'un rectangle de longueur \mathrm{L} et de largeur \mathrm{\ell} exprimées dans la même unité de longueur est : Longueur \times largeur = \mathrm{L} \times \ell.
- Remarque : Un carré est un rectangle particulier. Son aire se calcule donc de la même manière
que celle d'un rectangle: \mathcal{A} = côté \times côté = c \times c.
Exemples :
1. \mathrm{ABCD} est un rectangle de longueur 4~\mathrm{cm} et de largeur 3,5~\mathrm{cm}.
4 \times 3,5=14, donc l'aire du rectangle \mathrm{ABCD} est 14~\mathrm{cm}^2.
2. L'aire d'un carré de côté 5~\mathrm{cm} est 5~\mathrm{cm} \times 5~\mathrm{cm} = 25~\mathrm{cm}^2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Les volumes
Les solides usuels sont représentés ci-dessous. En classe de 6e, les calculs de volumes se
limitent aux assemblages de cubes.

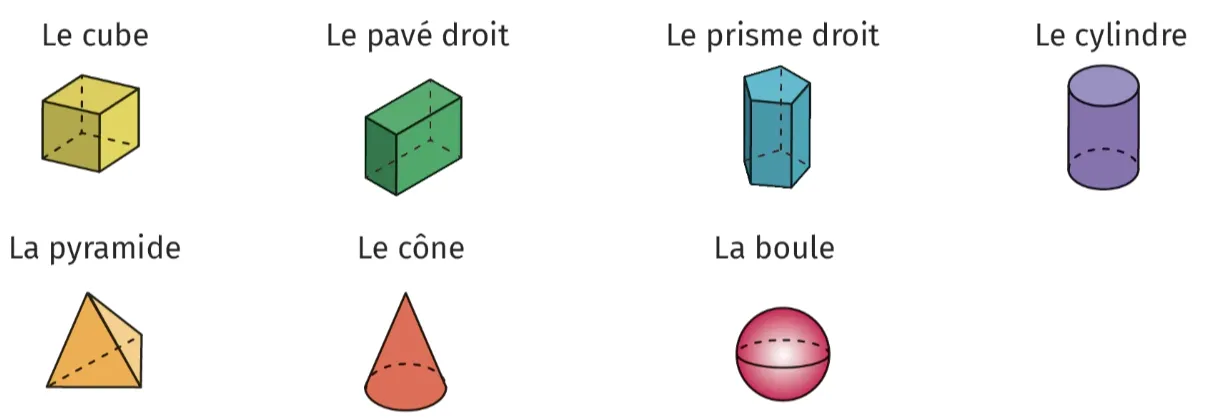
Le volume d'un solide est une grandeur correspondant à la place que l'objet occupe dans l'espace.
Le centimètre cube est l'unité de volume qui correspond au volume d'un cube dont l'arête mesure 1~\mathrm{cm}. Son symbole est : \mathrm{cm}^3.

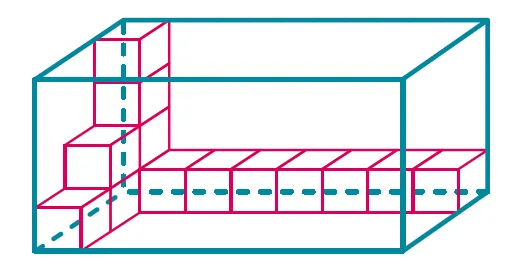


Définition
Le volume d'un solide est une grandeur correspondant à la place que l'objet occupe dans l'espace.
Définition
Le centimètre cube est l'unité de volume qui correspond au volume d'un cube dont l'arête mesure 1~\mathrm{cm}. Son symbole est : \mathrm{cm}^3.
Propriété
Pour déterminer le volume d'un assemblage, on doit déterminer
le nombre de cubes unités qui composent cet assemblage.


Exemple :

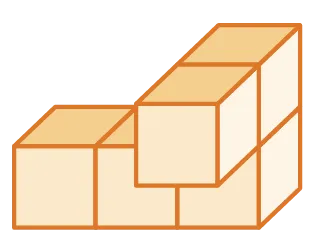
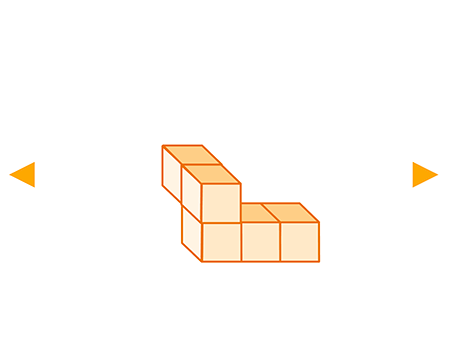
On veut déterminer le volume de l'assemblage ci-contre sachant
que chaque cube a un volume de 1~\mathrm{cm}^3. Cet assemblage est
composé de cinq cubes, donc son volume est : 5 \times 1~\mathrm{cm}^3 = 5~\mathrm{cm}^3.


- Remarque : Parmi deux assemblages, celui qui a le plus grand volume est celui qui est
composé du plus grand nombre de cubes unités.
Exemple :
On considère les assemblages de cubes unités suivants.
L'assemblage \mathrm{A} est composé de cinq cubes et l'assemblage \mathrm{B} est composé de six cubes. C'est donc l'assemblage \mathrm{B} qui a le plus grand volume.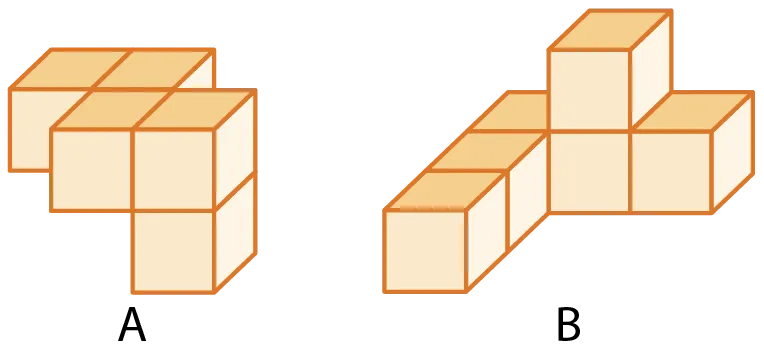
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille