Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 5
Exercices
Fonctions exponentielles et logarithme décimal
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fonctions exponentielles de base q
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1
Soit f la fonction définie par f(x) = 2,5^{x} sur
l'intervalle [-4 ; 4]. Répondre aux questions suivantes à l'aide d'un outil numérique.
1. Compléter le tableau de valeurs suivant.
2. Tracer la courbe représentative de la fonction f sur l᾽intervalle [-2 ; 2].
1. Compléter le tableau de valeurs suivant.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) |
2. Tracer la courbe représentative de la fonction f sur l᾽intervalle [-2 ; 2].
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2
Outil numérique
À l'aide d'un outil numérique, tracer la courbe représentative de chacune des fonctions suivantes sur l᾽intervalle [-1 ; 5] puis donner leur tableau de variations.
1. f(x) = 2^{x}
2. g(x) = 5^{-x}
1. f(x) = 2^{x}
2. g(x) = 5^{-x}
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3
Sans utiliser de calculatrice, classer ces listes de nombres dans l'ordre croissant.
1. 6,1^{1,1} ; 6,1^{1,4} ; 6,1^{1,2}.
2. 0,49^{0,7} ; 0,49^{2} ; 0,49^{-1,7}.
3. 3,14^{-9} ; 1 ; 3,14^{-5}.
1. 6,1^{1,1} ; 6,1^{1,4} ; 6,1^{1,2}.
2. 0,49^{0,7} ; 0,49^{2} ; 0,49^{-1,7}.
3. 3,14^{-9} ; 1 ; 3,14^{-5}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4
Dire si chacune des fonctions suivantes est croissante ou décroissante.
1. f(x)=7^{x}
2. g(x)=(\sqrt{2})^{x}
3. h(x)=\left(\frac{1}{3}\right)^{x}
4. i(x)=\left(\frac{5}{4}\right)^{x}
5. j(x)=1,1^{x}
6. k(x)=0,9^{x}
1. f(x)=7^{x}
2. g(x)=(\sqrt{2})^{x}
3. h(x)=\left(\frac{1}{3}\right)^{x}
4. i(x)=\left(\frac{5}{4}\right)^{x}
5. j(x)=1,1^{x}
6. k(x)=0,9^{x}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5
Le prix d'un article, dont le prix initial est de
100 euros, diminue de 7 % par an.
Modéliser le prix de cet article par une fonction exponentielle de base q.
Modéliser le prix de cet article par une fonction exponentielle de base q.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriétés opératoires des fonctions exponentielles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 6
Écrire les nombres suivants sous la forme d'une seule puissance de 3.
1. 3^{4} \times 9
2. \left(3^{0,5}\right)^{2}
3. \left(3^{1,5}\right)^{6} \times 3^{-3}
4. \left(3 \times 3^{3,5}\right)^{5}
1. 3^{4} \times 9
2. \left(3^{0,5}\right)^{2}
3. \left(3^{1,5}\right)^{6} \times 3^{-3}
4. \left(3 \times 3^{3,5}\right)^{5}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 7
Soit q un nombre réel strictement positif et
différent de 1. Simplifier les expressions suivantes.
1. \left(q^{6} \times q^{7}\right)^{2}
2. \left(q^{2}\right)^{-4}
3. q^{3} \times\left(q^{4}\right)^{5}
4. \frac{q^{8}}{q^{6}}
5. \frac{q^{8}}{\left(q^{2}\right)^{3}}
6. \frac{q^{5}}{q^{-4}}
7. \frac{\left(q^{3}\right)^{7}}{q^{-5}}
8. \frac{q^{5} \times q^{-3}}{q^{2}}
1. \left(q^{6} \times q^{7}\right)^{2}
2. \left(q^{2}\right)^{-4}
3. q^{3} \times\left(q^{4}\right)^{5}
4. \frac{q^{8}}{q^{6}}
5. \frac{q^{8}}{\left(q^{2}\right)^{3}}
6. \frac{q^{5}}{q^{-4}}
7. \frac{\left(q^{3}\right)^{7}}{q^{-5}}
8. \frac{q^{5} \times q^{-3}}{q^{2}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La fonction logarithme décimal
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 8
Outil numérique
Soit f la fonction définie par f(x)=\log (4 x) sur
l'intervalle [0,001 ; 10].
1. Compléter le tableau de valeurs suivant.
2. Tracer la courbe représentative de la fonction f.
3. Donner son tableau de variations sur [0,001 ; 10].
1. Compléter le tableau de valeurs suivant.
| x | 0,001 | 0,01 | 0,1 | 1 | 2 | 3 | 10 |
| f(x) |
2. Tracer la courbe représentative de la fonction f.
GeoGebra
3. Donner son tableau de variations sur [0,001 ; 10].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 9
Donner l'expression d'une fonction du type f(x)=\log (x)+a telle que f(1)=-1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 10
Laquelle de ces courbes représente la fonction logarithme décimal ? Justifier.
1.
Le zoom est accessible dans la version Premium.
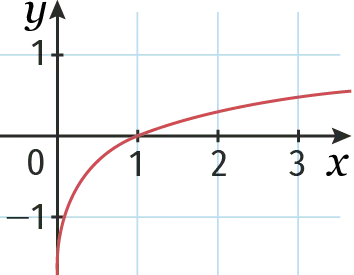
2.
Le zoom est accessible dans la version Premium.
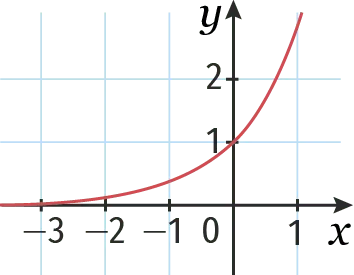
3.
Le zoom est accessible dans la version Premium.
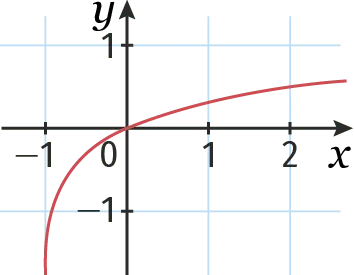
4.
Le zoom est accessible dans la version Premium.
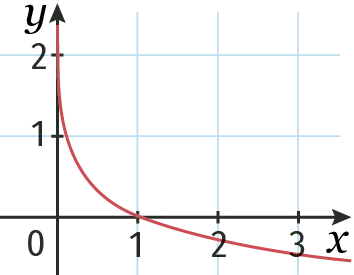
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriétés opératoires du logarithme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 11
Sans calculatrice, déterminer les valeurs de \log(1),
\log(10), \log(10^{-5}), \log(10\,000) et \log(0,000001).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 12
Exprimer en fonction de \log(x) et de \log(y)
les expressions suivantes, avec x et y des réels
strictement positifs.
1. \log \left(x^{4}\right)
2. \log \left(x^{-2}\right)
3. \log \left(x y^{3}\right)
4. \log \left(\frac{x^{3}}{y^{2}}\right)
1. \log \left(x^{4}\right)
2. \log \left(x^{-2}\right)
3. \log \left(x y^{3}\right)
4. \log \left(\frac{x^{3}}{y^{2}}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 13
Écrire les nombres suivants en fonction de \log(3).
1. \log(9)
2. \log(27)
3. \log(\frac{1}{3})
4. \log(30)
5. \log(300)
6. \log(0,003)
1. \log(9)
2. \log(27)
3. \log(\frac{1}{3})
4. \log(30)
5. \log(300)
6. \log(0,003)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 14
Lesquelles de ces valeurs sont négatives : \log(0,1), \log(1,001), \log \left(\frac{5}{4} \right) et \log \left(\frac{4}{5} \right) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Résolution d'équations et d'inéquations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 15
Résoudre les équations suivantes en détaillant
chaque étape. Donner la solution à 10^{-3} près.
1. 10^{x} = 2
2. 9^{x} = 5
3. 5^{x-2} = 12
4. \left(\frac{1}{2} \right)^{x} = 8
5. 4 \times 10^{x} - 18 = 0
1. 10^{x} = 2
2. 9^{x} = 5
3. 5^{x-2} = 12
4. \left(\frac{1}{2} \right)^{x} = 8
5. 4 \times 10^{x} - 18 = 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 16
Sans calculatrice, résoudre sur ] 0 ;+\infty[ les
équations suivantes.
1. \log(x) = 0
2. \log(x) = 1
3. \log(5x) = 0
4. \log(6x) = 1
5. \log(4x) -1 = 0
6. -7 \log(x) + 1 = 0
1. \log(x) = 0
2. \log(x) = 1
3. \log(5x) = 0
4. \log(6x) = 1
5. \log(4x) -1 = 0
6. -7 \log(x) + 1 = 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 17
Résoudre les inéquations suivantes sur \R.
1. 10^{x} \leqslant 1
2. 2^{x} \geqslant 2
3. 2^{x} \leqslant 5
4. \left(\frac{1}{2}\right)^{x} \geqslant 5
5. \left(\frac{2}{3}\right)^{x} \leqslant-1
6. 3^{x}+7 \geqslant 8
1. 10^{x} \leqslant 1
2. 2^{x} \geqslant 2
3. 2^{x} \leqslant 5
4. \left(\frac{1}{2}\right)^{x} \geqslant 5
5. \left(\frac{2}{3}\right)^{x} \leqslant-1
6. 3^{x}+7 \geqslant 8
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 18
Résoudre les inéquations suivantes sur ] 0 ;+\infty[.
1. \log (x) \leqslant 2
2. \log (x) \geqslant-2
3. 6+\log (x) \leqslant 3
4. 3 \log (x) \geqslant 15
1. \log (x) \leqslant 2
2. \log (x) \geqslant-2
3. 6+\log (x) \leqslant 3
4. 3 \log (x) \geqslant 15
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 19
Résoudre les inéquations suivantes sur ] 0 ;+\infty[.
1. 8 \log (x)>16+5 \log (x)
2. 5 \log \left(x^{2}\right)+3 \log (x) \lt 7
1. 8 \log (x)>16+5 \log (x)
2. 5 \log \left(x^{2}\right)+3 \log (x) \lt 7
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 20
Inversé
Donner une équation du type \log(x) = a
admettant 100 pour solution.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 21
Une onde sonore produit une pression acoustique x exprimée en pascal (Pa). Le niveau sonore correspondant, mesuré en décibel (dB), est donné par la fonction f définie par f(x)=20 \log \left(\frac{x}{p_{0}}\right), où p_{0} est une pression de référence correspondant à la plus petite intensité audible.
1. On donne p_{0}=10^{-4,7} Pa.
Montrer que f(x)=20 \log (x)+94.
2. La pression acoustique correspondant à une conversation humaine est de 0,07 Pa. Quel est, à l᾽unité près, le niveau sonore correspondant ?
3. Le seuil de douleur pour l'oreille humaine est de 120 dB. Calculer, à l᾽unité près, la pression acoustique correspondante.
4. Au-delà de 140 dB, les sons ne sont plus audibles par l'oreille humaine. Résoudre l'inéquation f(x) > 140 afin de déterminer à partir de quelle pression acoustique les sons ne sont plus audibles.
1. On donne p_{0}=10^{-4,7} Pa.
Montrer que f(x)=20 \log (x)+94.
2. La pression acoustique correspondant à une conversation humaine est de 0,07 Pa. Quel est, à l᾽unité près, le niveau sonore correspondant ?
3. Le seuil de douleur pour l'oreille humaine est de 120 dB. Calculer, à l᾽unité près, la pression acoustique correspondante.
4. Au-delà de 140 dB, les sons ne sont plus audibles par l'oreille humaine. Résoudre l'inéquation f(x) > 140 afin de déterminer à partir de quelle pression acoustique les sons ne sont plus audibles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 22
On étudie le nombre d'habitants d'un petit village situé à moins de 100 km de Paris et isolé des transports. Ce nombre est modélisé par la
fonction f définie sur l᾽intervalle [0 ; 11] par f(n)=400 \times 1,22^{n}, où n est le nombre d᾽années
après 2020. Ainsi, le nombre d᾽habitants en 2020 correspond à f(0).
Partie A : Étude de la fonction f
1. Déterminer le sens de variation de la fonction f sur l᾽intervalle [0 ; 11].
2. Dresser le tableau de variations de la fonction f sur l᾽intervalle [0 ; 11].
3. Compléter le tableau de valeurs suivant (les résultats seront arrondis à l'unité).
4. Tracer la courbe C représentative de la fonction f sur l'intervalle [0 ; 11].
Partie B : Application
5. Calculer, à l᾽unité près, le nombre d'habitants du village en 2025.
6. En utilisant le graphique de la Partie A, déterminer au bout de combien de temps la population aura doublé.
7. Résoudre algébriquement l᾽inéquation f(n) \geqslant 800 et retrouver le résultat de la question précédente.
Partie A : Étude de la fonction f
1. Déterminer le sens de variation de la fonction f sur l᾽intervalle [0 ; 11].
2. Dresser le tableau de variations de la fonction f sur l᾽intervalle [0 ; 11].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
3. Compléter le tableau de valeurs suivant (les résultats seront arrondis à l'unité).
| n | 0 | 2 | 4 | 6 | 8 | 10 | 11 |
| f(n) |
4. Tracer la courbe C représentative de la fonction f sur l'intervalle [0 ; 11].
GeoGebra
Partie B : Application
5. Calculer, à l᾽unité près, le nombre d'habitants du village en 2025.
6. En utilisant le graphique de la Partie A, déterminer au bout de combien de temps la population aura doublé.
7. Résoudre algébriquement l᾽inéquation f(n) \geqslant 800 et retrouver le résultat de la question précédente.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 23
L'intensité (ou magnitude) M sur l'échelle de Richter
d'un tremblement de terre est liée à l'énergie E (mesurée en joules) dissipée lors du tremblement de terre par la formule \log (\mathrm{E})=4,4+1,5 \times \mathrm{M}.
1. Calculer l'énergie dissipée lors du séisme à Valdivia au Chili en 1960 de magnitude 9,5 (séisme considéré comme le plus fort jamais enregistré). Donner le résultat sous la forme d᾽une écriture scientifique.
2. L᾽énorme explosion au port de Beyrouth au Liban, en 2020, correspond à un séisme de magnitude 4,5 sur l'échelle de Richter. Calculer l᾽énergie dissipée par cette explosion. Donner le résultat sous la forme d᾽une écriture scientifique.
3. Sachant qu'un kilo d'explosif (TNT) dissipe une énergie de 4,2 \times 10^6 joules, quelle est la valeur équivalente sur l'échelle de Richter, à l᾽unité près, d'une bombe H de 15 kilotonnes (bombe similaire à celle lâchée sur Hiroshima le 6 août 1945) ?
1. Calculer l'énergie dissipée lors du séisme à Valdivia au Chili en 1960 de magnitude 9,5 (séisme considéré comme le plus fort jamais enregistré). Donner le résultat sous la forme d᾽une écriture scientifique.
2. L᾽énorme explosion au port de Beyrouth au Liban, en 2020, correspond à un séisme de magnitude 4,5 sur l'échelle de Richter. Calculer l᾽énergie dissipée par cette explosion. Donner le résultat sous la forme d᾽une écriture scientifique.
3. Sachant qu'un kilo d'explosif (TNT) dissipe une énergie de 4,2 \times 10^6 joules, quelle est la valeur équivalente sur l'échelle de Richter, à l᾽unité près, d'une bombe H de 15 kilotonnes (bombe similaire à celle lâchée sur Hiroshima le 6 août 1945) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 24
Avant de pouvoir être utilisés, les outils médicaux doivent être stérilisés. Durant ce processus, ils sont soumis à une très forte chaleur, détruisant la grande majorité des germes présents à leur surface.
On considère qu'un outil est stérilisé quand moins d'un germe se trouve encore à sa surface.
1. On s'intéresse tout d'abord à une stérilisation à 125 °C. Dans ces conditions, le nombre N_{1} de germes présents sur cet outil en fonction du temps est donné, pour tout t > 0 en seconde, par la formule \mathrm{N}_{1}(t)=1000 \times 0,98^{t}.
a. Comment évolue le nombre de germes présents à la surface de l'objet durant ce processus ? Justifier.
b. Justifier que déterminer le temps nécessaire pour stériliser l'outil à l'aide de ce processus équivaut à résoudre l'inéquation 1000 \times 0,98^{t} \leqslant 1.
c. Résoudre cette inéquation en arrondissant le résultat au centième de seconde, puis interpréter ce résultat.
2. On s'intéresse maintenant à une stérilisation à 140 °C. Dans ces conditions, le nombre N_{2} de germes présents sur cet outil en fonction du temps est donné, pour tout t > 0 en seconde, par la formule \mathrm{N}_{2}(t)=1000 \times 0,84^{t}.
a. Au bout de combien de temps cet outil pourra‑t‑il être considéré comme stérilisé ? On arrondira le résultat au centième.
b. En déduire, entre 125 °C et 140 °C, laquelle de ces deux températures permet une stérilisation plus rapide des outils.
On considère qu'un outil est stérilisé quand moins d'un germe se trouve encore à sa surface.
1. On s'intéresse tout d'abord à une stérilisation à 125 °C. Dans ces conditions, le nombre N_{1} de germes présents sur cet outil en fonction du temps est donné, pour tout t > 0 en seconde, par la formule \mathrm{N}_{1}(t)=1000 \times 0,98^{t}.
a. Comment évolue le nombre de germes présents à la surface de l'objet durant ce processus ? Justifier.
b. Justifier que déterminer le temps nécessaire pour stériliser l'outil à l'aide de ce processus équivaut à résoudre l'inéquation 1000 \times 0,98^{t} \leqslant 1.
c. Résoudre cette inéquation en arrondissant le résultat au centième de seconde, puis interpréter ce résultat.
2. On s'intéresse maintenant à une stérilisation à 140 °C. Dans ces conditions, le nombre N_{2} de germes présents sur cet outil en fonction du temps est donné, pour tout t > 0 en seconde, par la formule \mathrm{N}_{2}(t)=1000 \times 0,84^{t}.
a. Au bout de combien de temps cet outil pourra‑t‑il être considéré comme stérilisé ? On arrondira le résultat au centième.
b. En déduire, entre 125 °C et 140 °C, laquelle de ces deux températures permet une stérilisation plus rapide des outils.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah