Pour un nombre \color{red}a donné, la fonction f qui associe à tout nombre x le nombre \color{red}a\color{black}x est une fonction linéaire. On écrit f: x \mapsto \color{red}a\color{black} x.
Le nombre \color{red}a est le coefficient de la fonction linéaire f.

La fonction f: x \mapsto \color{red}4\color{black} x est une fonction linéaire de coefficient 4.

Un tableau de valeurs d'une fonction linéaire est un tableau de proportionnalité.

Pour la fonction f: x \mapsto \color{red}4\color{black} x, on considère le tableau de valeurs suivant.

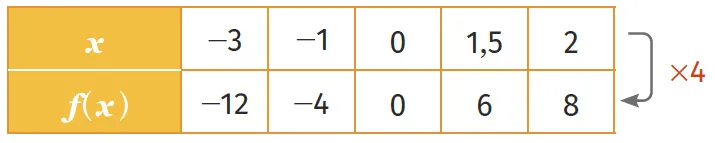
\color{red}a\color{black} = 4 est le coefficient de proportionnalité du tableau.

1.  Dans un repère, la courbe représentative d'une fonction linéaire est une droite passant par l'origine du repère.

2.  Dans un repère, toute droite non verticale passant par l'origine est la représentation graphique d'une fonction linéaire.

La courbe représentative de la fonction f: x \mapsto \color{red}4\color{black} x est la droite passant par l'origine et de coefficient directeur \color{red}4 (voir ci‑dessous).

• f est une fonction linéaire donc f(x)=a x.
• Grâce à cette expression, on peut exprimer f(4) en fonction de a.
• Comme f(4) est connu, on résout ensuite une équation d'inconnue a.

La fonction f est linéaire donc f(x)=a x.
En particulier, f(4)=a \times 4.
Comme f(4)=6, alors a \times 4=6.
D'où a=\frac{6}{4}=\frac{3}{2}.
Le coefficient de la fonction f est a=\frac{3}{2} donc f(x)=\frac{3}{2} x.

Représenter dans un repère la fonction linéaire f telle que f(x)=-3 x.

• La courbe représentative d'une fonction linéaire est une droite passant par l'origine du repère.
• Il suffit donc de trouver un second point de cette droite pour pouvoir la tracer.
• Pour cela, on calcule l'image d'un nombre. Par exemple, ici, on calcule f(1).

Une fonction linéaire est représentée par une droite passant par l'origine \text{O} du repère.
Comme f(\color{#F2B946}1\color{black})=-3 \times 1=\color{blue}-3\color{black}, la droite passe aussi par le point \mathrm{A}(\color{#F2B946}1\color{black} ;\color{blue}-3\color{black}).
La droite (\text{OA}) est donc la courbe représentative de la fonction f.

\color{red}a et \color{green}b sont deux nombres donnés. La fonction f qui associe à tout nombre x le nombre \color{red}a\color{black}x + \color{green}b est une fonction affine. On écrit {f: x \mapsto \color{red}a\color{black} x+\color{green}b}.
Les nombres \color{red}a et \color{green}b sont les paramètres de la fonction affine f.

La fonction f: x \mapsto \color{red}3\color{black} x-\color{green}2 est la fonction affine de paramètres \color{red}a = 3 et \color{green}b = -2.

Dans un repère, la courbe représentative d'une fonction affine est une droite.

Le nombre \color{red}a est le coefficient directeur de la droite. Le nombre \color{green}b est l'ordonnée à l'origine de la droite.

On considère la fonction f définie par f(x)=\color{red}3\color{black} x-\color{green}2.
Comme \color{green}-2 est l'ordonnée à l'origine, la courbe représentative de f est une droite (d) passant par le point \mathrm{A}(0 \: ;\color{green}-2\color{black}).
De plus, \color{red}a\color{black} = \color{red}3 est positif. Ainsi, lorsque x augmente de 1, f(x) augmente de 3.
Donc la droite (d) passe également par le point de coordonnées (0+1 \: ;-2+\color{red}3\color{black}), soit \mathrm{B}(1 \: ; 1).

On considère la fonction f définie par f(x)=\color{red}-2\color{black} x+\color{green}4.
Comme \color{green}4 est l'ordonnée à l'origine, la courbe représentative de f est une droite (d) passant par le point \mathrm{A}(0 \: ;\color{green}4\color{black}).
De plus, \color{red}a\color{black} = \color{red}-2 est négatif. Ainsi, lorsque x augmente de 1, f(x) diminue de 2.
Donc la droite (d) passe également par le point de coordonnées (0+1 \: ;4\color{red}-2\color{black}), soit \mathrm{B}(1 \: ; 2).

Dans un repère, tracer la courbe représentative de la fonction affine f: x \mapsto \frac{1}{3} x-1.

• La courbe représentative d'une fonction affine est une droite. Il suffit donc d'en connaître deux points pour pouvoir la tracer.
• On calcule les images de deux nombres pour obtenir ces deux points. Par exemple, ici, on calcule f(-3) et f(6).

Dans un repère, tracer la courbe représentative de la fonction affine f de paramètres a = -2 et b = 5.

• On place le point \mathrm{A}(0 \: ; \color{#5EB45E}b\color{black}).
• À partir du point \text{A}, on utilise le coefficient directeur pour trouver un second point. Quand x augmente de 1 unité, alors f(x) augmente ou diminue de \color{#CE422B}a unités (selon le signe de \color{#CE422B}a).

La courbe représentative de f est une droite (d). \color{#CE422B}a est le coefficient directeur de la droite (d) et \color{#5EB45E}b est son ordonnée à l'origine.
Ici, \color{#5EB45E}b\color{black} = \color{#5EB45E}5\color{black}. La droite (d) passe donc par le point \mathrm{A}(0 \: ; \color{#5EB45E}5\color{black}).
De plus, \color{#CE422B}a\color{black} = \color{#CE422B}-2\color{black} donc, à partir du point \text{A}, lorsque x augmente de 1, f(x) diminue de 2.
On obtient ainsi le point \mathrm{B}(1 \: ; 3).
On trace alors la droite (d) passant par les points \text{A} et \text{B}.