Mathématiques Terminale Bac Pro - Cahier
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 5
Activité A
Marketing viral
Capacité : Représenter graphiquement les fonctions exponentielles de base q.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Robin fait partie d'une société de production diffusant des vidéos sur Internet. En tant que directeur marketing, l'une de ses missions est d'étudier le taux d'engagement de ces vidéos publiées sur les réseaux sociaux.
Le taux d'engagement d'une vidéo est un nombre réel R représentant le nombre moyen de partage de cette dernière par un internaute. Ainsi, par exemple, si une vidéo a un taux d'engagement de R = 3 cela signifie que, en moyenne, un internaute partage cette dernière avec trois de ses contacts, qui le partagent eux-même avec trois des leurs, et ainsi de suite. Dans cette activité on va considérer, pour simplifier, qu'une vidéo de cette société n'est diffusée, pour commencer, qu'à un seul internaute.
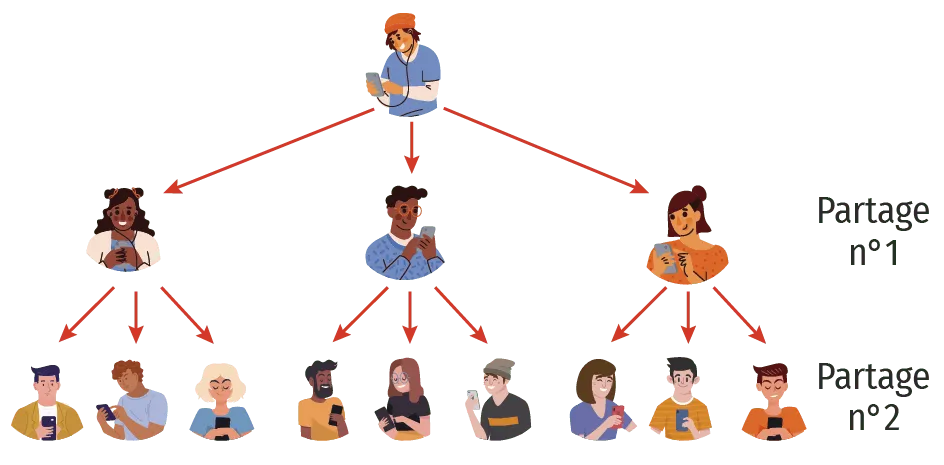
Le taux d'engagement d'une vidéo est un nombre réel R représentant le nombre moyen de partage de cette dernière par un internaute. Ainsi, par exemple, si une vidéo a un taux d'engagement de R = 3 cela signifie que, en moyenne, un internaute partage cette dernière avec trois de ses contacts, qui le partagent eux-même avec trois des leurs, et ainsi de suite. Dans cette activité on va considérer, pour simplifier, qu'une vidéo de cette société n'est diffusée, pour commencer, qu'à un seul internaute.
Problématique
Quelles valeurs de taux d'engagement Robin vise‑t‑il ?
Quelles valeurs voudrait‑il éviter ?
Quelles valeurs voudrait‑il éviter ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Robin s'intéresse à une vidéo de taux d'engagement R = 3.
a. Analyser / Raisonner
Avec combien de personnes sera partagée cette vidéo lors de la première vague de partages ? Avec combien de personne sera‑t‑elle partagée lors de la deuxième vague ?
b. Analyser / Raisonner
Pour tout entier n \geqslant 1, on note u_{n} nombre de personnes avec qui cette vidéo est partagée lors de la n-ième vague de partages. La suite (u_{n}) est alors géométrique. Préciser sa raison.
c. Valider
Exprimer u_{n} en fonction de n.
a. Analyser / Raisonner
Avec combien de personnes sera partagée cette vidéo lors de la première vague de partages ? Avec combien de personne sera‑t‑elle partagée lors de la deuxième vague ?
b. Analyser / Raisonner
Pour tout entier n \geqslant 1, on note u_{n} nombre de personnes avec qui cette vidéo est partagée lors de la n-ième vague de partages. La suite (u_{n}) est alors géométrique. Préciser sa raison.
c. Valider
Exprimer u_{n} en fonction de n.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Robin s'intéresse aussi à deux autres vidéos : une de taux d'engagement R = 1{,}1 et une autre de taux d'engagement R = 0{,}8.
a. S'approprier
Télécharger . Quelle formule doit‑on entrer dans la cellule B3 pour obtenir, en étirant vers le bas, les valeurs des cellules B4 à B7 ?
b. Réaliser Remplir la feuille de calcul puis tracer, pour chacune de ces trois vidéos, un nuage de points représentant le nombre d'internautes avec qui elle est partagée en fonction du nombre de vagues de partages.
c. Analyser / Raisonner Que peut‑on dire du nuage de points correspondant à la vidéo de taux d'engagement R = 1{,}1 ? Que peut‑on dire de celui correspondant à celle de taux d'engagement R = 0{,}8 ?
d. S'approprier À l'aide de la calculatrice, déterminer le nombre d'internautes avec lesquels la vidéo de taux d'engagement R = 1{,}1 sera partagée lors de la 30e vague de partages. Arrondir ce nombre à l'unité.
a. S'approprier
Télécharger . Quelle formule doit‑on entrer dans la cellule B3 pour obtenir, en étirant vers le bas, les valeurs des cellules B4 à B7 ?
b. Réaliser Remplir la feuille de calcul puis tracer, pour chacune de ces trois vidéos, un nuage de points représentant le nombre d'internautes avec qui elle est partagée en fonction du nombre de vagues de partages.
c. Analyser / Raisonner Que peut‑on dire du nuage de points correspondant à la vidéo de taux d'engagement R = 1{,}1 ? Que peut‑on dire de celui correspondant à celle de taux d'engagement R = 0{,}8 ?
d. S'approprier À l'aide de la calculatrice, déterminer le nombre d'internautes avec lesquels la vidéo de taux d'engagement R = 1{,}1 sera partagée lors de la 30e vague de partages. Arrondir ce nombre à l'unité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Communiquer
Après avoir testé plusieurs autres taux d'engagement différents, répondre à la problématique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
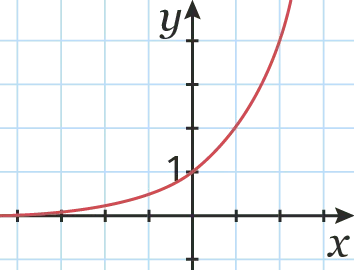
La fonction qui, à tout réel x, associe q^{x}, avec q \neq 1 et q>0, est appelée
fonction .
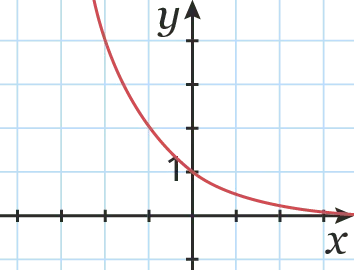
- Si q > 1, la fonction est
sur \R.
- Si 0 \lt q \lt 1 , la fonction est sur \R.
Remarque
La fonction f définie
par f(x) = q^{x} est constante égale à si q = 1.
Pour s᾽entraîner :
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
