Chapitre 7
Exercices
Vecteurs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Vecteurs et coordonnées
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1

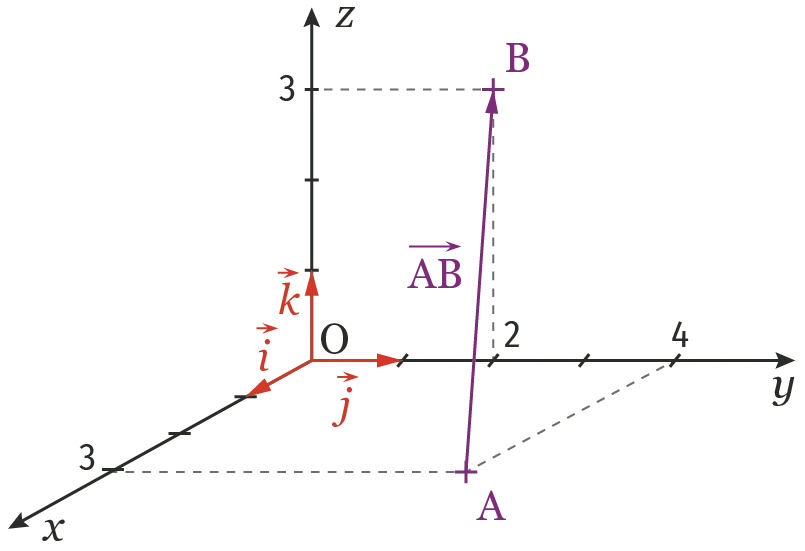
1. Déterminer graphiquement les coordonnées du vecteur \overrightarrow{\textrm{AB}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2
1.
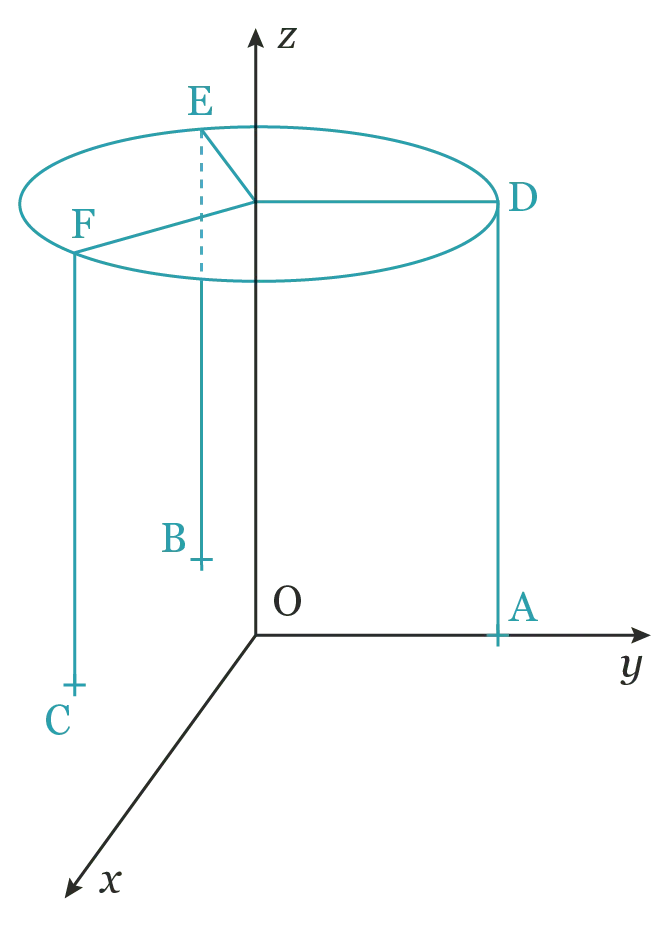
Dans un repère orthonormé (\mathrm{O} \: ; \vec{i}, \vec{j}, \vec{k}), placer les points suivants de coordonnées \mathrm{A}(0 \: ; 1 \: ; 0), \mathrm{B}(3 \: ; 1 \: ; 0), \mathrm{C}(3 \: ; 3 \: ; 0), \mathrm{D}(3 \: ; 1 \: ; 2), \mathrm{E}(3 \: ; 3 \: ; 2), \mathrm{F}(0 \: ; 3 \: ; 0), \mathrm{G}(0 \: ; 1 \: ; 2) et \mathrm{H}(0 \: ; 3 \: ; 2).
2. De quel solide ces points sont-ils les sommets ?
2. De quel solide ces points sont-ils les sommets ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3
1.
Dans un repère orthonormé (\mathrm{O} \: ; \vec{i}, \vec{j}, \vec{k}), placer le point \text{A} de coordonnées \mathrm{A}(0 \: ; 2 \: ; 2).
2. Représenter le vecteur \overrightarrow{\mathrm{AB}}\left(\begin{array}{c} 2 \\ -2 \\ -1 \end{array}\right).
2. Représenter le vecteur \overrightarrow{\mathrm{AB}}\left(\begin{array}{c} 2 \\ -2 \\ -1 \end{array}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4
Copie d᾽élève
Voici l'énoncé de l'exercice réalisé par Lisa :
On donne les points \text{A} et \text{B} de coordonnées \mathrm{A}(0 \: ; 2 \: ; 2) et \mathrm{B}(1 \: ; 0 \: ; 0).
Calculer les coordonnées du vecteur \overrightarrow{\textrm{AB}}.
Voici la copie de Lisa :
Indiquer l'erreur dans la copie de Lisa et proposer une correction.
On donne les points \text{A} et \text{B} de coordonnées \mathrm{A}(0 \: ; 2 \: ; 2) et \mathrm{B}(1 \: ; 0 \: ; 0).
Calculer les coordonnées du vecteur \overrightarrow{\textrm{AB}}.
Voici la copie de Lisa :
Les coordonnées de \overrightarrow{\mathrm{AB}} sont \left(\begin{array}{l}
0-1 \\
2-0 \\
2-0
\end{array}\right)=\left(\begin{array}{c}
-1 \\
2 \\
2
\end{array}\right)
Indiquer l'erreur dans la copie de Lisa et proposer une correction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5
Déterminer les coordonnées du vecteur \overrightarrow{\mathrm{AB}} dans les cas suivants.
1. \mathrm{A}(5 \: ; 3 \: ; 2) et \mathrm{B}(6 \: ; 4,5 \: ; 10).
2. \mathrm{A}(-1 \: ; 4,2 \: ; 1) et \mathrm{B}(7 \: ; 8 \: ; -3).
3. \mathrm{A}(5 \: ; 7,1 \: ; -5) et \mathrm{B}(-2 \: ; -0,9 \: ; 3).
4. \mathrm{A}(0 \: ; 1 \: ; -2) et \mathrm{B}(-2 \: ; 0 \: ; 3,75).
1. \mathrm{A}(5 \: ; 3 \: ; 2) et \mathrm{B}(6 \: ; 4,5 \: ; 10).
2. \mathrm{A}(-1 \: ; 4,2 \: ; 1) et \mathrm{B}(7 \: ; 8 \: ; -3).
3. \mathrm{A}(5 \: ; 7,1 \: ; -5) et \mathrm{B}(-2 \: ; -0,9 \: ; 3).
4. \mathrm{A}(0 \: ; 1 \: ; -2) et \mathrm{B}(-2 \: ; 0 \: ; 3,75).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Vecteurs et normes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 6
Le plan est rapporté à un repère orthonormé (\mathrm{O} \: ; \vec{i}, \vec{j}, \vec{k}). On considère les points \mathrm{A}(2 \: ; 0 \: ; 3), \mathrm{B}(0 \: ; -1 \: ; 2), \mathrm{C}(0 \: ; 1 \: ; 1) et \mathrm{D}(-1 \: ; 1 \: ; 1).
1. Calculer les coordonnées des vecteurs \overrightarrow{\textrm{AB}}, \overrightarrow{\textrm{AC}} et \overrightarrow{\textrm{AD}}.
2. Calculer la norme des vecteurs \overrightarrow{\textrm{AB}}, \overrightarrow{\textrm{AC}} et \overrightarrow{\textrm{AD}}.
1. Calculer les coordonnées des vecteurs \overrightarrow{\textrm{AB}}, \overrightarrow{\textrm{AC}} et \overrightarrow{\textrm{AD}}.
2. Calculer la norme des vecteurs \overrightarrow{\textrm{AB}}, \overrightarrow{\textrm{AC}} et \overrightarrow{\textrm{AD}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 7
Algorithmique
1.
Que fait la fonction Python vecteur ci-dessous ?
2. À l'aide de cette fonction Python, vérifier les réponses obtenues à la question 1. de l'.
def vecteur(xA, yA, zA, xB, yB, zB) x = xB - xA y = yB - yA z = zB - zA return (x, y, z)
2. À l'aide de cette fonction Python, vérifier les réponses obtenues à la question 1. de l'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 8
On se place dans un repère orthonormé.
1. Calculer, au dixième près, les normes des vecteurs suivants.
a. \overrightarrow{\mathrm{AB}}\left(\begin{array}{c} 25 \\ 58 \\ -6 \end{array}\right)
b. \overrightarrow{\mathrm{CD}}\left(\begin{array}{l} 3 \\ 1 \\ 2 \end{array}\right)
c. \overrightarrow{\mathrm{AD}}\left(\begin{array}{c} 50 \\ 116 \\ -12 \end{array}\right)
2. Quelle conclusion peut-on en tirer concernant les vecteurs \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{AD}} ?
3. Justifier que \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{AD}} sont colinéaires.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 9
Copie d᾽élève
Voici l'énoncé de l'exercice réalisé par Nabil :
Dans un repère orthonormé, on considère les points \text{C} et \text{G} de coordonnées \mathrm{C}(24 \: ;-42 \: ; 12) et \mathrm{G}(48 \: ;-86 \: ; -26).
1. Calculer les coordonnées du vecteur \overrightarrow{\mathrm{CG}}.
2. Calculer la norme du vecteur \overrightarrow{\mathrm{CG}}.
Voici la copie de Nabil :
1. Les coordonnées du vecteur : \overrightarrow{\mathrm{CG}} sont \left(\begin{array}{c}
24 \\
44 \\
-38
\end{array}\right).
2. La norme du vecteur \overrightarrow{\mathrm{CG}} est \|\overrightarrow{\mathrm{CG}}\|=3956 \text { . }
2. La norme du vecteur \overrightarrow{\mathrm{CG}} est \|\overrightarrow{\mathrm{CG}}\|=3956 \text { . }
Indiquer les erreurs dans la copie de Nabil et proposer une correction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 10
Algorithmique
Le programme ci-dessous ne fonctionne pas.
1. Trouver et corriger l'erreur commise dans ce programme.
2. Qu'obtient-on alors en sortie de ce programme ?
from math import *
def norme(x, y, z):
n = x**2 + y**2 + z**2
return(x)
print("La norme du vecteur est : ", norme (50, 116, -12))
1. Trouver et corriger l'erreur commise dans ce programme.
2. Qu'obtient-on alors en sortie de ce programme ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Somme de deux vecteurs, vecteurs égaux ou colinéaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 11
Copie d᾽élève
Voici l'énoncé de l'exercice réalisé par Marco :
On considère les vecteurs \overrightarrow{\mathrm{AB}}\left(\begin{array}{c}
30 \\
16 \\
-2
\end{array}\right) et \overrightarrow{\mathrm{BC}}\left(\begin{array}{l}
8 \\
6 \\
8
\end{array}\right).
Calculer les coordonnées du vecteur \overrightarrow{\mathrm{EF}}=\overrightarrow{\mathrm{AB}}+3 \times \overrightarrow{\mathrm{BC}}.
Calculer les coordonnées du vecteur \overrightarrow{\mathrm{EF}}=\overrightarrow{\mathrm{AB}}+3 \times \overrightarrow{\mathrm{BC}}.
Voici la copie de Marco :
On a \left(\begin{array}{c}
x_{\overrightarrow{\mathrm{EF}}} \\
y_{\overrightarrow{\mathrm{EF}}} \\
z_{\overrightarrow{\mathrm{EF}}}
\end{array}\right)=\left(\begin{array}{c}
30+3 \times 8 \\
16+6 \\
-2+8
\end{array}\right)=\left(\begin{array}{c}
54 \\
22 \\
6
\end{array}\right).
Indiquer les erreurs commises par Marco puis les corriger.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 12
Dans un repère orthonormé (\mathrm{O} \: ; \vec{i}, \vec{j}, \vec{k}), on considère les points suivants :
\mathrm{A}(-7 \: ; 8 \: ; 2), \mathrm{B}(-1 \: ; 1 \: ; 9) et \mathrm{C}(2 \: ; 4 \: ; 2).
1. Déterminer les coordonnées des vecteurs \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{AC}}.
2. Calculer les normes des deux vecteurs \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{AC}}.
3. Déterminer les coordonnées du vecteur \overrightarrow{\mathrm{CF}} tel que {\overrightarrow{\mathrm{CF}}=2 \times \overrightarrow{\mathrm{AB}}+3 \times \overrightarrow{\mathrm{AC}}}.
4. Calculer la norme du vecteur \overrightarrow{\mathrm{CF}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 13
On considère les vecteurs \overrightarrow{\mathrm{AB}}\left(\begin{array}{c}
58 \\
-15 \\
120
\end{array}\right) et \overrightarrow{\mathrm{CD}}\left(\begin{array}{c}
-47 \\
25 \\
-250
\end{array}\right).
Déterminer les coordonnées du vecteur \overrightarrow{\mathrm{PX}} tel que \overrightarrow{\mathrm{PX}}=2 \times \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CD}}.
Déterminer les coordonnées du vecteur \overrightarrow{\mathrm{PX}} tel que \overrightarrow{\mathrm{PX}}=2 \times \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CD}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 14
Déterminer les coordonnées du vecteur \overrightarrow{\mathrm{AC}} dans les cas suivants.
1. \overrightarrow{\mathrm{AB}}\left(\begin{array}{c} -2 \\ 3 \\ 4 \end{array}\right) et \overrightarrow{\mathrm{BC}}\left(\begin{array}{l} 4 \\ 6 \\ 8 \end{array}\right).
2. \overrightarrow{\mathrm{AB}}\left(\begin{array}{c} 5 \\ 0 \\ -2 \end{array}\right) et \overrightarrow{\mathrm{BC}}\left(\begin{array}{c} 6 \\ 4 \\ -1,5 \end{array}\right).
3. \overrightarrow{\mathrm{AB}}\left(\begin{array}{c} 4,1 \\ 3 \\ -2 \end{array}\right) et \overrightarrow{\mathrm{BC}}\left(\begin{array}{c} 2 \\ -1 \\ -3 \end{array}\right).
1. \overrightarrow{\mathrm{AB}}\left(\begin{array}{c} -2 \\ 3 \\ 4 \end{array}\right) et \overrightarrow{\mathrm{BC}}\left(\begin{array}{l} 4 \\ 6 \\ 8 \end{array}\right).
2. \overrightarrow{\mathrm{AB}}\left(\begin{array}{c} 5 \\ 0 \\ -2 \end{array}\right) et \overrightarrow{\mathrm{BC}}\left(\begin{array}{c} 6 \\ 4 \\ -1,5 \end{array}\right).
3. \overrightarrow{\mathrm{AB}}\left(\begin{array}{c} 4,1 \\ 3 \\ -2 \end{array}\right) et \overrightarrow{\mathrm{BC}}\left(\begin{array}{c} 2 \\ -1 \\ -3 \end{array}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 15


Un silo à grains permet de stocker des aliments pour les animaux d'élevage. On a représenté ci-dessous, dans un repère orthonormé d'axes , un trépied servant de support à un tel silo. L'unité de ce repère est le centimètre.

Les coordonnées des points de ce schéma sont \mathrm{A}(0 \: ; 125 \: ; 0), \mathrm{B}(-110 \: ; -63 \: ; 0), \mathrm{C}(110 \: ; -63 \: ; 0), \mathrm{D}(0 \: ; 125 \: ; 500), \mathrm{E}(-110 \: ; -63 \: ; 500) et \mathrm{F}(110 \: ; -63 \: ; 500).
1. Déterminer les coordonnées des vecteurs \overrightarrow{\mathrm{AD}}, \overrightarrow{\mathrm{BE}} et \overrightarrow{\mathrm{CF}}.
2. Déterminer la norme des vecteurs \overrightarrow{\mathrm{AD}}, \overrightarrow{\mathrm{BE}} et \overrightarrow{\mathrm{CF}}.
3. Que peut-on conclure ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 16


Galubina vient de la planète Montasa (\textrm{M}) où il a volé des documents secrets comportant les plans de l'Empire. Ces documents donnent des indications concernant une base secrète (\textrm{B}).
Sur son parcours, il fait une escale sur Carbonatus (\textrm{C}) pour faire le plein de carburant et récupérer son droïde C2HO. Il doit se rendre ensuite sur la planète Orthogona (\textrm{O}) où se trouve le siège de la résistance et le gouverneur Gaïa pour remettre les documents. Malheureusement, sur le trajet, il se fait attaquer par les troupes de Dark Vektor. Il doit dévier de sa trajectoire et passer par Nixus (\textrm{N}) pour rejoindre Orthogona (\textrm{O}).
Sur les documents secrets sont consignées les différentes coordonnées des planètes. Toutes ces coordonnées sont données par rapport à Orthogona (\textrm{O}). Les valeurs des coordonnées sont exprimées en millions de kilomètres.
| Planètes | Coordonnées |
|---|---|
| Orthogona (\textrm{O}) | (0 \: ; 0 \: ; 0) |
| Montasa (\textrm{M}) | (-50 \: ; 104 \: ; 152) |
| Carbonatus (\textrm{C}) | (34 \: ; 25 \: ; -9) |
| Nixus (\textrm{N}) | (35 \: ; -10 \: ; 100) |
| Plutark (\textrm{P}) | (29 \: ; 146 \: ; 57) |
Sur ces documents secrets, on découvre aussi la position de la base secrète avec l'indication suivante : {\overrightarrow{\mathrm{PB}}=2 \times \overrightarrow{\mathrm{CN}}-\frac{1}{2} \overrightarrow{\mathrm{MO}}}.
1. Écrire le trajet de Galubina à l'aide d'une somme de vecteurs.
2. Calculer les coordonnées de chaque vecteur du parcours.
3. Quelle est la distance parcourue par Galubina pour se rendre de Montasa à Orthogona à l'unité près ?
4. Quelle est la position de la base secrète ?
5. À quelle distance se situe-t-elle d᾽Orthogona à l'unité près ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

