Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 4
Exercices
Fonctions polynômes de degré 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La fonction cube
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1
Effectuer, sans calculatrice, les calculs suivants.
1. 4^3
2. 3^3
3. 0^3
4. (-1)^3
5. (-3)^3
1. 4^3
2. 3^3
3. 0^3
4. (-1)^3
5. (-3)^3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2
Soit f la fonction définie par f(x)=2 x^{3}. Calculer les images suivantes.
1. f(-2)
2. f(-1)
3. f(0)
4. f(1)
1. f(-2)
2. f(-1)
3. f(0)
4. f(1)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3
Voici les représentations graphiques de trois fonctions polynômes de degré 3.
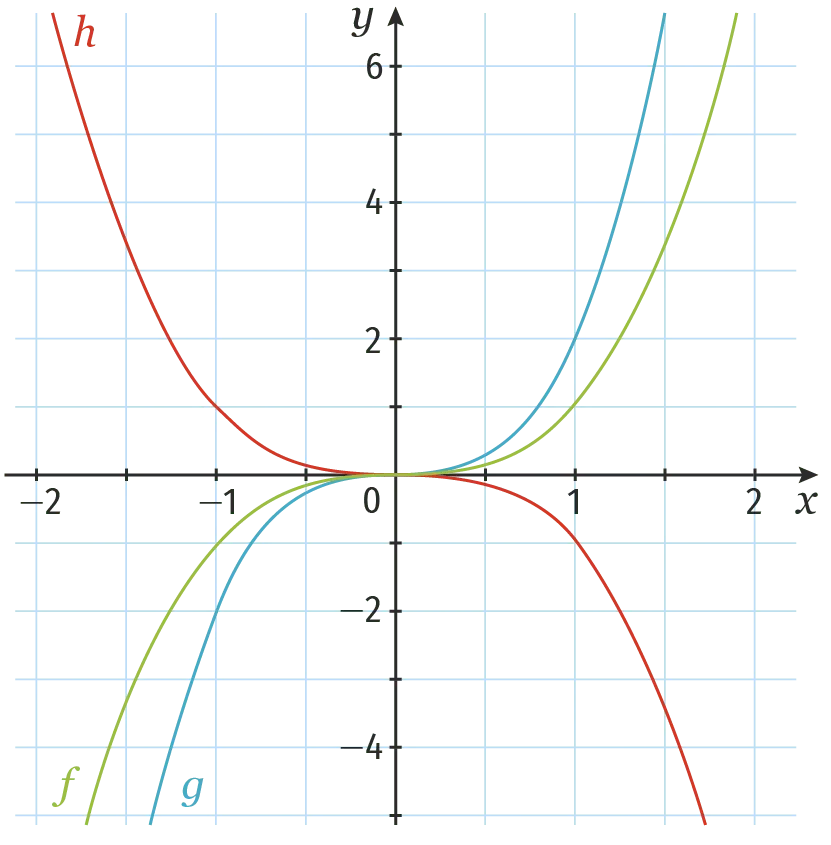
Associer à chaque fonction son expression.
1. 2x^3
2. -x^3
3. x^3
Le zoom est accessible dans la version Premium.
Associer à chaque fonction son expression.
1. 2x^3
2. -x^3
3. x^3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4
Outil numérique
Pierre désire utiliser un tableur afin de calculer les images de la fonction f définie sur \Reals par f(x)=5 x^{3}.
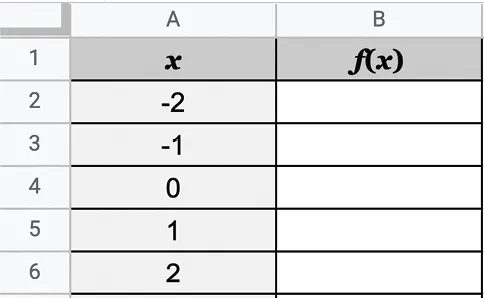
1. Quelle formule devra-t-il écrire dans la cellule B2 ?
2. Ouvrir une feuille de calcul, recopier le tableau ci-dessus puis calculer les images de x par la fonction f.
3. Que constate-t-on ?
Le zoom est accessible dans la version Premium.
1. Quelle formule devra-t-il écrire dans la cellule B2 ?
2. Ouvrir une feuille de calcul, recopier le tableau ci-dessus puis calculer les images de x par la fonction f.
3. Que constate-t-on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5
Inversé
On considère une fonction f dont un tableau de valeurs est donné ci-dessous.
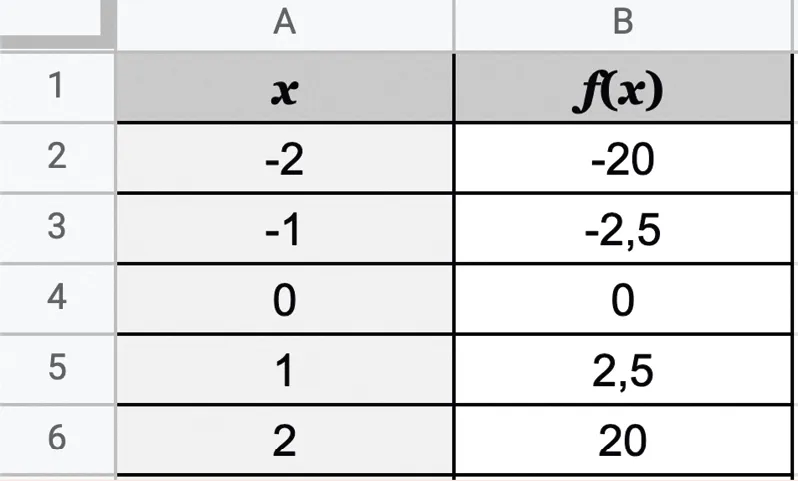
En sachant que f est une fonction polynôme de degré 3 du type ax^3, déterminer l'expression de la fonction f.
Le zoom est accessible dans la version Premium.
En sachant que f est une fonction polynôme de degré 3 du type ax^3, déterminer l'expression de la fonction f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étude de fonctions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 6
Déterminer les expressions des fonctions dérivées des fonctions suivantes.
1. f(x)=x^{3}+x^{2}+x+1
2. g(x)=2 x^{3}+4 x^{2}+6 x+10
3. h(x)=-4 x^{2}+6 x-7 x^{3}
4. i(x)=(x-1)(x+2)(2 x-4)
5. j(t)=t(t-4)^{2}
1. f(x)=x^{3}+x^{2}+x+1
2. g(x)=2 x^{3}+4 x^{2}+6 x+10
3. h(x)=-4 x^{2}+6 x-7 x^{3}
4. i(x)=(x-1)(x+2)(2 x-4)
5. j(t)=t(t-4)^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 7
Soit g la fonction dont la courbe représentative est tracée en bleue dans le repère suivant.
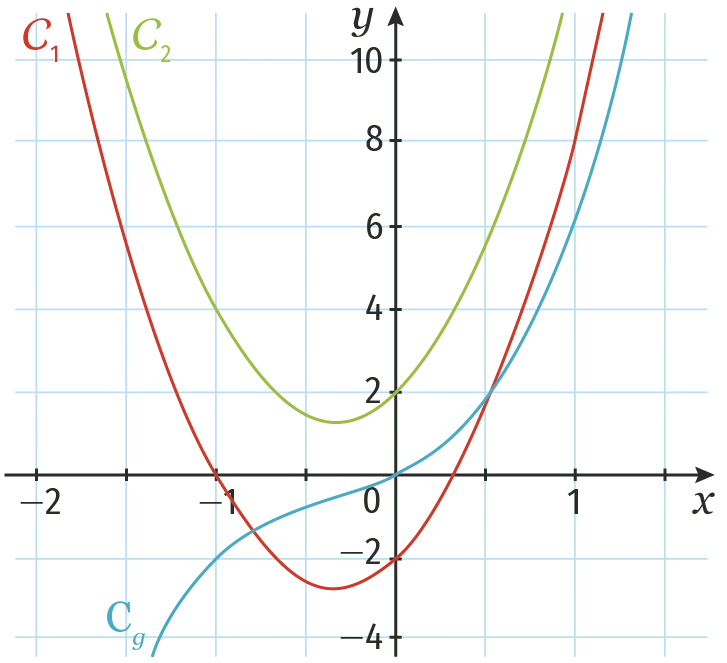
Déterminer, parmi les courbes C_1 et C_2, laquelle représente la fonction dérivée g'. Justifier.
Le zoom est accessible dans la version Premium.
Déterminer, parmi les courbes C_1 et C_2, laquelle représente la fonction dérivée g'. Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 8
Copie d'élève
Soit f une fonction qui admet comme fonction dérivée la fonction f' telle que, pour tout x \in[-10\: ; 10], f^{\prime}(x)=-3(x+1)(x-4).
Étudier le signe de f' et dresser le tableau de variations de la fonction f sur l᾽intervalle [-10\:; 10].
Un élève propose la réponse suivante :
Indiquer les erreurs dans la copie et proposer une correction.
Étudier le signe de f' et dresser le tableau de variations de la fonction f sur l᾽intervalle [-10\:; 10].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Un élève propose la réponse suivante :
Le zoom est accessible dans la version Premium.
Indiquer les erreurs dans la copie et proposer une correction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 9
Outil numérique
Soit f la fonction définie sur [-5\:; 2] par :
1. Tracer la courbe représentative de la fonction f.
2. Dresser le tableau de variations de la fonction f sur [-5\:; 2].
3. La fonction f admet-elle des extremums locaux ? Si oui, donner leurs coordonnées.
f(x)=-\frac{2}{3} x^{3}-2 x^{2}+6 x+3.
1. Tracer la courbe représentative de la fonction f.
GeoGebra
2. Dresser le tableau de variations de la fonction f sur [-5\:; 2].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
3. La fonction f admet-elle des extremums locaux ? Si oui, donner leurs coordonnées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Nombre de solutions d'une équation à l'aide d'un tableau de variations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 10
Copie d᾽élève
Soit f une fonction définie sur [-6\:; 2] admettant le tableau de variations suivant.
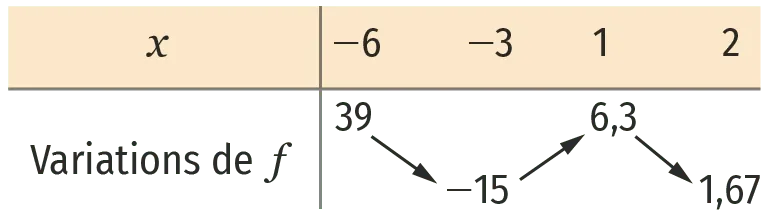
Combien de solutions l'équation f(x)=0 admet-elle ?
Un élève propose la réponse suivante :
Indiquer les erreurs dans la copie et proposer une correction.
Le zoom est accessible dans la version Premium.
Combien de solutions l'équation f(x)=0 admet-elle ?
Un élève propose la réponse suivante :
Le zoom est accessible dans la version Premium.
Indiquer les erreurs dans la copie et proposer une correction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 11
Outil numérique
Soit f la fonction définie sur [0\:; 3] par :
1. Tracer la courbe représentative de la fonction f.
2. Dresser le tableau de variations de la fonction f sur [0\:; 3]. Arrondir les valeurs au dixième si besoin.
3. En déduire le nombre de solutions de l'équation f(x)=0 sur [0\:; 3].
4. À l'aide de la courbe de la question 1., déterminer une valeur approchée, au dixième près, des solutions de l'équation f(x)=0.
f(x)=-x^{3}-x^{2}+10.
1. Tracer la courbe représentative de la fonction f.
GeoGebra
2. Dresser le tableau de variations de la fonction f sur [0\:; 3]. Arrondir les valeurs au dixième si besoin.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
3. En déduire le nombre de solutions de l'équation f(x)=0 sur [0\:; 3].
4. À l'aide de la courbe de la question 1., déterminer une valeur approchée, au dixième près, des solutions de l'équation f(x)=0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 12
Outil numérique
Soit g la fonction définie sur [0\:; 4] par :
1. Calculer g(1).
2. Tracer la courbe représentative de la fonction g.
3. À l'aide de la courbe représentative, dresser le tableau de variations de la fonction g sur [0\:; 4].
4. a. À l'aide du tableau de variations, donner le nombre de solutions de l'équation g(x)=0{,}5.
b. À l'aide de la courbe de la question 2., déterminer une valeur approchée, au dixième près, des solutions de l'équation g(x)=0{,}5.
g(x)=x^{3}-6 x^{2}+9 x-3.
1. Calculer g(1).
2. Tracer la courbe représentative de la fonction g.
GeoGebra
3. À l'aide de la courbe représentative, dresser le tableau de variations de la fonction g sur [0\:; 4].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
4. a. À l'aide du tableau de variations, donner le nombre de solutions de l'équation g(x)=0{,}5.
b. À l'aide de la courbe de la question 2., déterminer une valeur approchée, au dixième près, des solutions de l'équation g(x)=0{,}5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 13
Outil numérique
On cherche à déterminer le nombre de solutions de l'équation x^3 - x^2 = 1 sur [-2\:;2].
Soit f la fonction définie sur [-2\:;2] par f(x) = x^3 - x^2.
1. Déterminer l'expression de f', la dérivée de la fonction f.
2. Tracer la courbe représentative de la fonction f'.
3. À l'aide de cette courbe représentative, construire le tableau de variations de la fonction f sur [-2\:;2].
4. En déduire le nombre de solutions de l'équation x^{3}-x^{2}=1 sur [-2\:;2].
Soit f la fonction définie sur [-2\:;2] par f(x) = x^3 - x^2.
1. Déterminer l'expression de f', la dérivée de la fonction f.
2. Tracer la courbe représentative de la fonction f'.
GeoGebra
3. À l'aide de cette courbe représentative, construire le tableau de variations de la fonction f sur [-2\:;2].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
4. En déduire le nombre de solutions de l'équation x^{3}-x^{2}=1 sur [-2\:;2].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 14
Leslie souhaite préparer un gâteau pour l'anniversaire de son fils.
La recette indique qu'il faut faire cuire le gâteau à 150 °C \pm 5 % durant quinze minutes. La température du four ne doit pas être supérieure à la température maximale indiquée durant plus de deux minutes, ou inférieure à la température minimale indiquée durant plus de quatre minutes, sinon le gâteau sera mal cuit. L'évolution de la température f(t) du four (en degré Celsius) en fonction du temps t (en minute) est donnée par f(t)=0,1 t^{3}-3,7 t^{2}+42,4 t.
Problématique : Le gâteau de Leslie sera-t-il réussi ?
1. Calculer les températures minimales et maximales pour une bonne cuisson du gâteau.
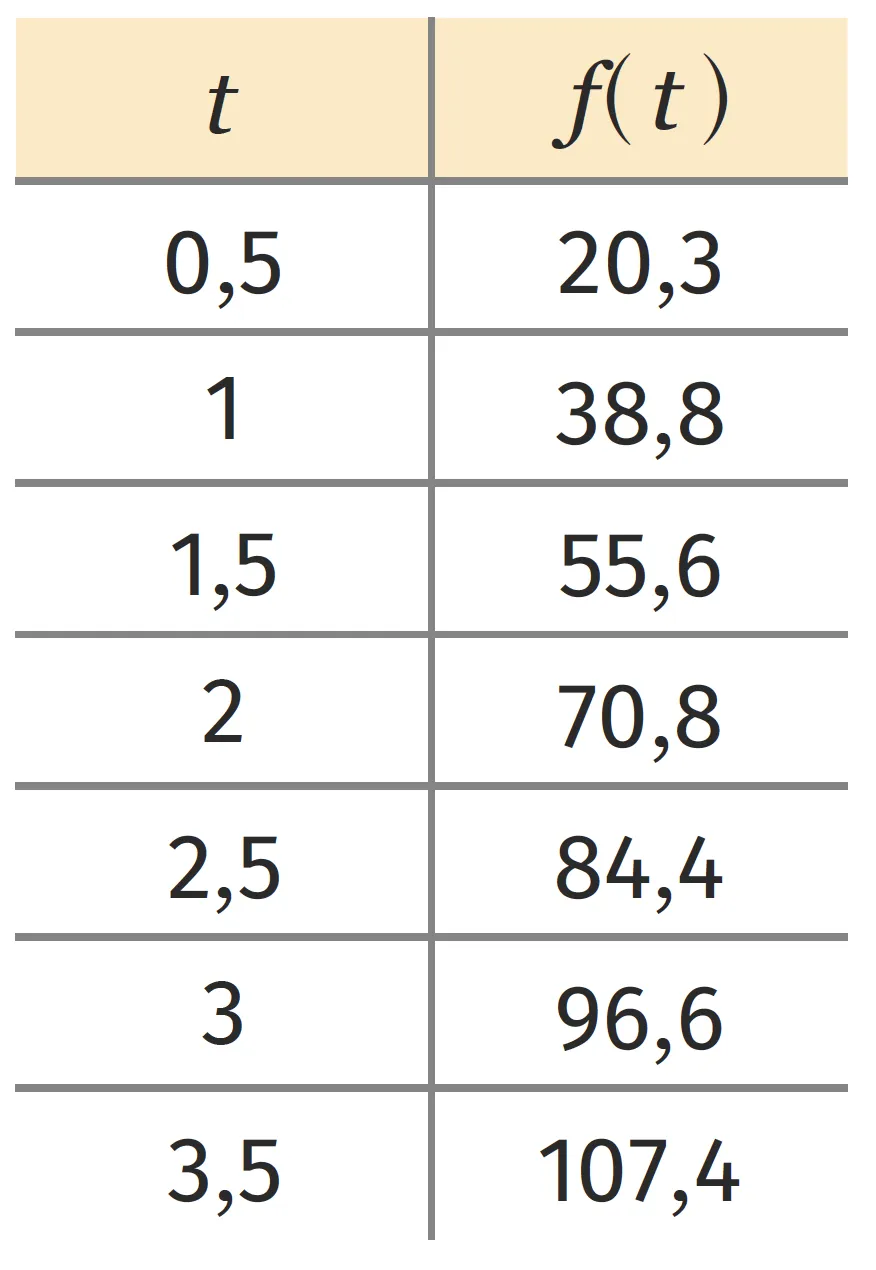
2. À l'aide du tableau de valeurs suivant, donner un encadrement du temps nécessaire afin que le four atteigne la température minimale désirée.
3. Déterminer l'expression de f', fonction dérivée de la fonction f.
4. Dresser le tableau de signe de la fonction f' sur [6\:;21] en arrondissant les racines à 0,01 près.
5. Dresser le tableau de variations de la fonction f sur [6\:;21].
6. En déduire les coordonnées des extremums de la fonction f sur [6\:;21].
7. Peut-on alors être certain que le gâteau sera réussi ? Justifier.
8. Tracer la représentation graphique de la fonction f sur l'intervalle [6\:;21].
9. Répondre à la problématique.
La recette indique qu'il faut faire cuire le gâteau à 150 °C \pm 5 % durant quinze minutes. La température du four ne doit pas être supérieure à la température maximale indiquée durant plus de deux minutes, ou inférieure à la température minimale indiquée durant plus de quatre minutes, sinon le gâteau sera mal cuit. L'évolution de la température f(t) du four (en degré Celsius) en fonction du temps t (en minute) est donnée par f(t)=0,1 t^{3}-3,7 t^{2}+42,4 t.
Problématique : Le gâteau de Leslie sera-t-il réussi ?
1. Calculer les températures minimales et maximales pour une bonne cuisson du gâteau.
2. À l'aide du tableau de valeurs suivant, donner un encadrement du temps nécessaire afin que le four atteigne la température minimale désirée.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
3. Déterminer l'expression de f', fonction dérivée de la fonction f.
4. Dresser le tableau de signe de la fonction f' sur [6\:;21] en arrondissant les racines à 0,01 près.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
5. Dresser le tableau de variations de la fonction f sur [6\:;21].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
6. En déduire les coordonnées des extremums de la fonction f sur [6\:;21].
7. Peut-on alors être certain que le gâteau sera réussi ? Justifier.
8. Tracer la représentation graphique de la fonction f sur l'intervalle [6\:;21].
GeoGebra
9. Répondre à la problématique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 15
Copie d'élève
L'évolution du bénéfice b, en euro, d'une entreprise en fonction de ses ventes est donnée par la fonction définie par b(x)=-3 x^{3}+125 x^{2}-500 x+2000, où x représente le nombre d'articles vendus.
Étudier l'évolution du bénéfice de l'entreprise en fonction de ses ventes sur l'intervalle [0\:;35].
Arrondir les résultats à l'unité.
Un élève propose la réponse suivante.
Indiquer les erreurs dans la copie et proposer une correction.
Étudier l'évolution du bénéfice de l'entreprise en fonction de ses ventes sur l'intervalle [0\:;35].
Arrondir les résultats à l'unité.
Un élève propose la réponse suivante.
Le zoom est accessible dans la version Premium.
Indiquer les erreurs dans la copie et proposer une correction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 16
Outil numérique
Utiliser un tableur afin de donner un encadrement à 0,1 près des solutions sur [-2\:;1] de l'équation {(2 x+3)(5 x-1)^{2}=4}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 17
Inversé
Soit f une fonction polynôme de degré 3 admettant trois racines x_1=-2, x_2=1 et x_3=4.
Donner une expression possible de la fonction f sous la forme ax^3 + bx^2 + cx + d.
Donner une expression possible de la fonction f sous la forme ax^3 + bx^2 + cx + d.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah