Numération
Séquence 23
Comprendre les fractions unitaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Identifier et nommer une fraction d'un tout partagé en parts égales
- Savoir interpréter, représenter, écrire et lire les fractions \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \frac{1}{8} et \frac{1}{10}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Percevoir qu'une partie d'un tout fractionné en parts égales plus petites est un objet mathématique permettra d'aborder plus tard les notions de fraction d'unités, fractions décimales et nombres décimaux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Connaître les termes « demi », « moitié » et « quart » dans des situations de partage d'un tout en parts égales
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'enseignement débute par des fractions unitaires afin que les élèves comprennent qu'une partie d'un tout est à envisager comme un objet spécifique. Nous expliquons ce que représente une fraction unitaire en montrant et en partageant plusieurs formes, bandes ou figures en parts égales afin que les élèves ne restent pas sur une version prototypée de la fraction. De plus, il est important de toujours se référer au tout quand on représente une fraction pour ancrer une bonne compréhension de ce concept chez les élèves. La séance 2 est construite en ce sens. Nous faisons donc le choix d'introduire les écritures chiffrées seulement en fin de séance 2, afin de mettre l'accent sur la compréhension du concept mathématique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Séance 1
60 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Comprendre le demi, la moitié et le quart
Projeter et distribuer la carte rituel P2-18. Demander aux élèves d'entourer les représentations correctes d'un demi et d'un quart, puis faire représenter un demi, une moitié et un quart en coloriant les figures.
Corriger devant les élèves et faire expliciter les réponses.Différenciation
Distribuer des gabarits pour que les élèves puissent fractionner par pliage.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème additif à une étape
Au cinéma, des personnes sont déjà installées. Un groupe de 23 personnes arrive. 30 personnes sont maintenant dans la salle. Cherche le nombre de personnes installées avant que le groupe arrive.Quelle situation correspond à l'énoncé ?
Projeter le problème intercalaire et les situations proposées. Échanger sur celle qui correspond à l'énoncé et en expliciter les raisons.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif de la séance
- Reconnaître et représenter les fractions unitaires \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \frac{1}{8} et \frac{1}{10} et leur écriture
Matériel de la séance
- Les affiches de la séquence 11
- 3 à 5 bandes de papier d'environ 30 cm par binôme
- Ressource numérique à projeter
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Lancement de la séance
Collectif
5 min
Afin de rappeler ce que sont un demi et un quart, faire réfléchir l'ensemble de la classe durant une minute, puis solliciter au moins deux élèves pour expliciter. « En début d'année, vous avez appris à partager des formes, des bandes, des gâteaux, etc., en deux ou quatre parts égales. Vous savez que la part s'appelle un demi ou une moitié lorsque l'on partage en deux parts égales, et un quart lorsque l'on coupe en quatre parts égales. » S'appuyer sur les affiches réalisées en séquence 11.Collectif
5 min
Annoncer l'objectif : « Aujourd'hui, vous allez apprendre à représenter d'autres fractions. »


Laisser les élèves s'exprimer et noter les mots-clés de leurs réponses au tableau (partager, parties, parts, morceaux, égaux, etc.).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Recherche : partage en parts égales
En binômes
10 min
En binômes
10 min
Situation-problème
Pour une même bande, proposer différents partages en parts égales.
Point didactique
Il est choisi de ne pas présenter directement aux élèves des bandes fractionnées, mais plutôt de faire émerger plusieurs fractionnements différents, pour leur faire percevoir que la fraction d'un tout correspond à un objet à part entière, d'abord perceptible, puis symbolisé par une écriture mathématique à partir de la séance 2. Il s'agit également de leur faire prendre conscience qu'un même tout peut être fractionné en parts égales de différentes façons.
Faire reformuler la consigne par un élève puis montrer en exemple une bande fractionnée en deux, en indiquant qu'elle est partagée en deux parts égales, qui sont deux demis. Préciser qu'il faut produire d'autres partages que celui-ci.
Circuler pour vérifier que les partages sont réalisés en parts égales. Si besoin, arrêter la recherche au bout de quelques minutes et demander à un binôme de montrer à la classe comment partager une bande par pliage.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Mise en commun
Collectif
8 min
Demander aux binômes de présenter leur méthode et recenser tous les partages trouvés.Collectif
8 min
Lorsqu'un binôme indique comment il a partagé sa bande, la placer au tableau en verbalisant : « Vous avez partagé la bande en X parts égales. » Si certains partages n'ont pas été proposés, ce qui sera sûrement le cas des partages en 5 et en 10, les présenter aux élèves et afficher les bandes au tableau.
Préciser que ces partages ont été effectués à la règle graduée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Institutionnalisation
Collectif
7 min
« Nous avons fractionné les bandes en 2, 3, 4, 5, 6, 8 et 10 parts égales. Si on colorie une seule partie de la bande fractionnée en quatre, comment s'appellera cette partie ? »Collectif
7 min
Colorier un quart.
« C'est une partie de la bande fractionnée en quatre. Cela s'appelle un quart. Un quart, c'est une fraction de cette bande coupée en quatre morceaux. Ces autres parts sont aussi des quarts. Il y a quatre quarts dans une bande entière. »
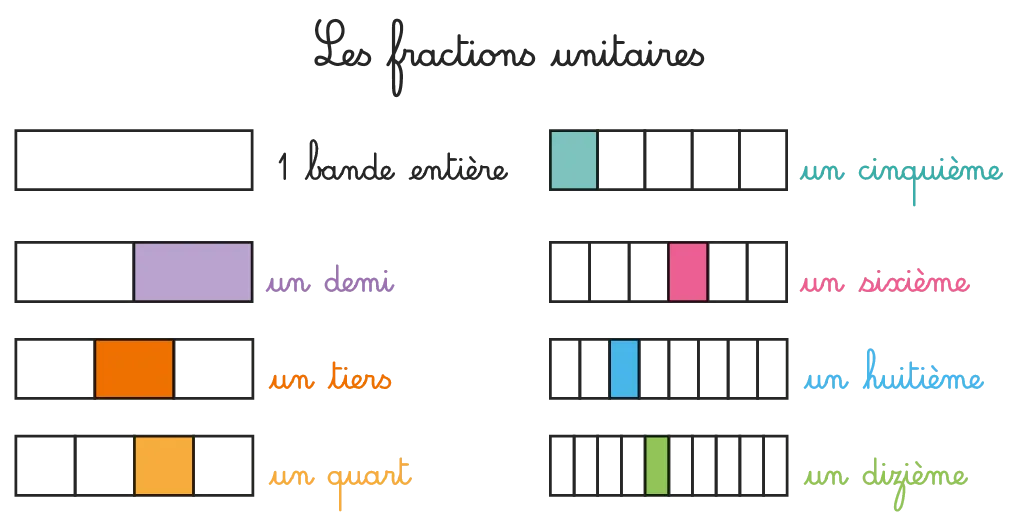
Réitérer cette verbalisation avec les élèves pour les autres fractions. La trace écrite sera la photo du tableau nommée « Les fractions unitaires ». Expliciter que ce terme désigne une partie d'un tout partagé en parts égales. Conserver les bandes pour les séances suivantes.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Pratique guidée
Individuel
5 min
Projeter l'image « Reconnaître des fractions ».Individuel
5 min
Pour chaque représentation, les élèves choisissent le nom correspondant à la fraction. Valider en faisant justifier la réponse correcte après chaque question.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Bilan
En binômes et individuel
5 min
En binômes et individuel
5 min
- Synthèse mathématique « Qu'avez-vous appris durant cette séance ? »
- Bilan de l'apprentissage Les élèves complètent oralement ou dans leur cahier d'apprentissage l'affirmation suivante : « Durant cette séance, j'ai aimé... »
Les élèves réfléchissent seuls, puis à deux.
Réponse attendue en revenant à la cible : une définition du terme « fraction » et comment les représenter.


Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

