Déterminer la moitié des nombres pairs de 2 à 30

Tout nombre entier est soit pair soit impair. La parité peut se modéliser « 2n » : tout nombre pair est égal à 2 ou un multiple de 2. À la fin de l'année, les élèves doivent connaitre les moitiés des nombres pairs de 2 à 30. Ils s'appuient en priorité sur les doubles, mais apprennent aussi comment « partager un nombre en 2 ». La méthode pour calculer la moitié d'un nombre impair de dizaines sera travaillée en profondeur en période 3.
Il n'est pas impossible d'aborder la question de la moitié de nombres impairs. On expliquera aux élèves qu'il est possible de calculer que la moitié de 5 est « deux et demi », mais qu'ils l'apprendront plus tard dans leur scolarité.

Projeter la carte rituel P2-17. Faire ordonner les nombres par ordre croissant.

Corriger devant les élèves et faire expliciter les réponses.

Variable didactique
Faire ranger les nombres 457, 258, 478, 978, 256, 477 et 302 dans l'ordre décroissant.

Sur le présentoir de la bibliothèque, il y a 125 livres, dont 46 albums et 62 bandes dessinées, le reste étant constitué de livres documentaires. Cherche combien il y a de livres documentaires.

Projeter le problème intercalaire et les démarches de résolution proposées. Échanger sur celle qui correspond au problème résolu et en expliciter les raisons.

Faire le lien avec le travail réalisé sur les doubles, puis annoncer l'objectif du jour : « Vous avez révisé et appris les doubles des nombres de 1 à 15, 25, 35, 45. Aujourd'hui, vous allez apprendre à calculer la moitié d'un nombre pair inférieur à 20. »

« Qu'est-ce que la moitié d'un nombre ? » Laisser les élèves réfléchir une minute avant de recueillir au moins deux réponses.

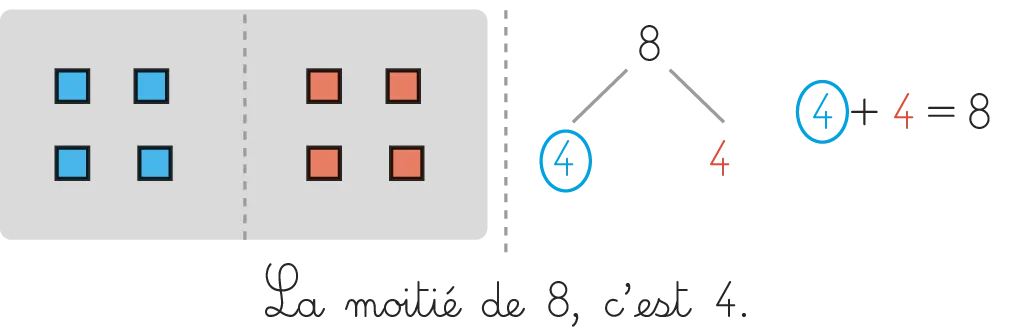
« La moitié, c'est l'une des deux parties d'un tout une fois que celui-ci est partagé en deux parts égales. Par exemple, la moitié de huit cubes est quatre cubes, car si on partage huit cubes en deux, on met quatre cubes d'un côté et quatre cubes de l'autre. Il y a exactement la même quantité de cubes de chaque côté. La moitié d'un disque, c'est un côté de disque coupé en deux parties égales. La moitié d'une heure, c'est la moitié de l'horloge, la moitié de 60 minutes, c'est-à-dire 30 minutes. Pour trouver la moitié d'un nombre, on peut s'aider des doubles. Si on sait que 4 plus 4 est égal à 8, on sait que la moitié de 8 est 4. »

Exercice intercalaire : Que cherche-t-on ?

• 
  Combien d'enfants vont jouer.
• 
  La moitié de 14.
• 
  Le double de 14.

Valider la bonne réponse.
Laisser les élèves travailler dans leur cahier de recherche. Des jetons peuvent être mis à disposition.

Corriger en faisant expliquer les différentes procédures utilisées :

• s'appuyer sur l'addition « 7 + 7 = 14 » ;
• s'appuyer sur la décomposition « 14 = 10 + 4 » et additionner la moitié de 10 et la moitié de 4 ;
• rendre 14 jetons et partager en deux en répartissant les jetons un par un.

Modeler en s'appuyant sur des représentations.
« Vous avez calculé la moitié de 14. Si vous vous souvenez que 14 est le double de 7, alors vous savez que la moitié de 14 est 7. Si vous ne vous rappelez pas le double, vous pouvez prendre 14 jetons et les partager en deux. »

Construire un affichage reprenant ces représentations.
Introduire la notion de nombre pair : « Est-ce qu'on peut calculer la moitié de tous les nombres ? »

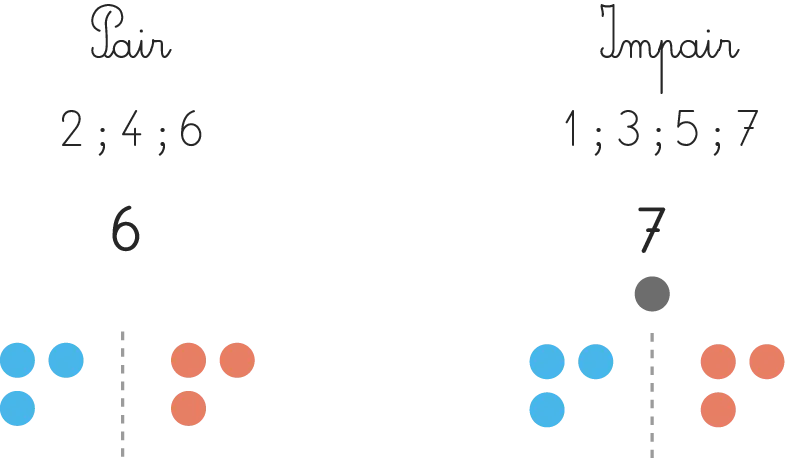
Tracer un tableau avec une colonne « Pair » et « Impair » puis essayer de partager le chiffre 1 en deux. Prendre un jeton. Dire que, puisqu'on ne peut pas le couper, on ne peut pas encore trouver sa moitié. Écrire 1 dans la colonne « Impair ». Prendre deux jetons et montrer qu'on peut en mettre un de chaque côté, donc que la moitié de 2 est 1. Écrire 2 dans la colonne « Pair ». Continuer ainsi jusqu'à 20. Relire les nombres contenus dans chaque colonne du tableau et faire émerger les notions de nombres pairs et impairs.

« Vous pouvez calculer la moitié des nombres qui finissent par 0, 2, 4, 6, 8. On les appelle les "nombres pairs". Si le nombre finit par 1, 3, 5, 7 ou 9, c'est un "nombre impair" et on ne peut pas trouver sa moitié car on ne peut pas le partager en deux parts égales pour l'instant. »

Rappeler la procédure pour déterminer la moitié d'un nombre pair qui a été vue lors du modelage. La trace écrite sera constituée de cette procédure ainsi que des représentations déjà présentes sur l'affichage.

Projeter la page 54 du fichier et donner les consignes.

• Synthèse mathématique
« Qu'avez-vous appris durant cette séance ? »
Les élèves réfléchissent seuls, puis à deux.
Réponse attendue en revenant à la cible : les termes « moitié », « nombres pairs » et « impairs » et leur signification. Le lien entre la moitié et le double.

• Bilan de l'apprentissage
Les élèves complètent oralement ou dans leur cahier d'apprentissage l'affirmation suivante : « Ce que j'ai appris me servira en dehors de l'école, car... »

Les tables des multiplications par 3 et 4
« J'ai... Qui a ? » : faire jouer les élèves durant dix minutes (explications p. 104).

Problème additif à deux étapes : recherche du tout
Dans une rue, il y a 56 voitures garées. 19 s'en vont et 29 se garent à nouveau. Combien de voitures sont garées ?
Quelle démarche a été utilisée ?

Projeter le problème intercalaire et les démarches de résolution proposées. Échanger sur celle qui correspond au problème résolu et en expliciter les raisons.

Afin de rappeler la procédure utilisée en séance 1, faire réfléchir l'ensemble de la classe durant une minute, puis solliciter au moins deux élèves pour l'expliciter.
« Aujourd'hui, vous allez vous entrainer à calculer la moitié des nombres pairs entre 20 et 30. »

Calculer la moitié des nombres pairs entre 2 et 30.

Exercice intercalaire : Que cherche-t-on ?

• La moitié des 26 cahiers.
• Le nombre de paquets de cahiers pour une maitresse.
• Le nombre de cahiers par élève.

Valider la bonne réponse puis laisser les élèves travailler dans leur cahier de recherche.

Corriger en faisant expliciter les différentes procédures utilisées le cas échéant. Insister sur la lenteur de l'utilisation des jetons à répartir un par un lorsque les nombres sont plus grands. Présenter les deux procédures suivantes (avec l'outil « Ardoise maths » pour la première).

Projeter la page 55 du fichier et donner les consignes de l'exercice 1.
Circuler pour valider les procédures des élèves en réussite et aider ceux qui en ont besoin.

Pour chaque nombre, un élève explique sa procédure. Veiller à ce que les deux procédures soient présentées.
Garder une trace des deux procédures sur une affiche.
Demander à combien est égale la moitié de 30. Vérifier avec des cubes emboitables : fabriquer trois dizaines, en mettre une à droite, l'autre à gauche, puis casser la dernière et la répartir de chaque côté. Constater que la moitié de 30 est 15.

Projeter la page 55 du fichier et donner les consignes pour les exercices suivants.

• Synthèse mathématique
« Qu'avez-vous appris durant cette séance ? »
Les élèves réfléchissent seuls, puis à deux.
Réponse attendue en revenant à la cible : calculer la moitié d'un nombre pair entre 20 et 30.

• Bilan de l'apprentissage
Les élèves complètent oralement ou dans leur cahier d'apprentissage l'affirmation suivante : « Pour trouver la moitié d'un nombre pair, je peux... »