Thème 3 : Espace et géométrie
Problèmes transversaux
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Entiers, décimaux
Le professeur de mathématiques a verrouillé son casier à l'aide d'un cadenas à code à deux chiffres. Il a laissé sur son bureau des indices pour le retrouver au cas où il l'oublierait. Pour cela, il doit retrouver la valeur des chiffres \mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E} et \mathrm{F} grâce aux indications suivantes.
Le code est :
- \mathrm{A} est le chiffre des unités de milliers de 531~246.
- \mathrm{B} est le chiffre des millièmes de 1~245,386~1.
- \mathrm{C} est le chiffre des centaines de la somme de 4~048,351 et 251,68.
- \mathrm{D} est le chiffre des centièmes de la différence de 12~431,43 et 25,589.
- \mathrm{E} est le chiffre des dix-millièmes du produit de 3,48 et 1,76.
- \mathrm{F} est le reste de la division euclidienne de 1~614 par 12.
Cliquez ici pour avoir accès à un espace de dessin
Le code est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Fractions, proportionnalité
Christophe prépare un gâteau pour ses enfants Lou, Adam et Mathilde.
Lou en mange \frac{2}{5}, Adam en prend 3 parts sur 10 et Mathilde en mange 20~\%.
1. a. Écrire la part mangée par chacun sous la forme de fractions de dénominateur 10.
b. Qui a mangé le plus de gâteau ?
2. Quelle part du gâteau restera-t-il ?
3. La recette du gâteau prévoyait 165 grammes de sucre. Quelle quantité de sucre chaque enfant aurait-il mangé si Christophe avait suivi la recette ?
4. Pour réduire les apports en sucre, Christophe décide de diviser les quantités de sucre par 5. Quelle quantité de sucre chaque enfant a-t-il alors mangée ?
Lou en mange \frac{2}{5}, Adam en prend 3 parts sur 10 et Mathilde en mange 20~\%.
1. a. Écrire la part mangée par chacun sous la forme de fractions de dénominateur 10.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Fractions, décimaux
Paolo est malade. Le médecin lui prescrit un traitement à prendre à l'aide d'une seringue graduée en mg de médicament.
1. Le médecin lui prescrit 4,4~\mathrm{mg} de médicament trois fois par jour pendant une semaine.
a. Quelle quantité de médicament doit-il prendre chaque jour ?
b. Le flacon récupéré en pharmacie contient 100~\mathrm{mg} de médicament. Est-ce suffisant pour 7 jours ?
c. En lisant la notice, Paolo apprend qu'il faut prendre au maximum 0,35~\mathrm{mg} de médicament par jour et par kg. Paolo pèse 40,2~\mathrm{kg}. Vérifier que la prescription du médecin respecte bien le dosage journalier.
1. Le médecin lui prescrit 4,4~\mathrm{mg} de médicament trois fois par jour pendant une semaine.
a. Quelle quantité de médicament doit-il prendre chaque jour ?
2. La mère de Paolo regarde la seringue graduée fournie dans la boîte. Compléter l'égalité qui permettra de trouver la graduation adaptée sur la seringue, puis la colorier.
4,4 = \frac{\ldots}{10} = \frac{\ldots}{5} = \ldots + \frac{\ldots}{\ldots}
4,4 = \frac{\ldots}{10} = \frac{\ldots}{5} = \ldots + \frac{\ldots}{\ldots}
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Décimaux, proportionnalité
Hakim, Diane et leurs deux enfants vont au restaurant avec Nathalie, Eric et leurs quatre enfants. On indiquera les calculs en bas de page.
1. Compléter la facture.
2. Tous hésitent au moment de régler l'addition.
a. Certains proposent que chaque famille paye proportionnellement au nombre de personnes la composant. Compléter le tableau suivant afin de déterminer la part de chaque famille.
b. D'autres proposent de partager l'addition en deux parts égales. Calculer le prix à payer pour chaque famille.
1. Compléter la facture.
| Désignation | Prix unitaire | Quantité | Prix |
|---|---|---|---|
| Steak-frites | 12,90~\euro | 6 | |
| Gâteau | 6~\euro | 18~\euro | |
| Glace | 3 | 16,20~\euro | |
| Menu complet | 27,50~\euro | 4 | |
| Café | 4 | 5,20~\euro | |
| Total |
2. Tous hésitent au moment de régler l'addition.
a. Certains proposent que chaque famille paye proportionnellement au nombre de personnes la composant. Compléter le tableau suivant afin de déterminer la part de chaque famille.
| Total | Passage à l'unité | Famille Hakim et Diane | Famille Eric et Nathalie | |
|---|---|---|---|---|
| Nombre de personnes | 1 | |||
| Prix à payer |
b. D'autres proposent de partager l'addition en deux parts égales. Calculer le prix à payer pour chaque famille.
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Périmètre, durées, calculs astucieux
En 208 ap. J.‑C., Marcus et Appia participent à une course de chars dans le cirque romain d'Arles représenté ci-dessous.


La course s'effectue en 7 tours de piste.
1. Calculer le périmètre de la piste, puis la distance parcourue par les chevaux. On arrondira au mètre près.
2. À chaque tour, on note les temps du char de Marcus.
Calculer astucieusement la durée totale de la course de Marcus.
3. Appia a fini la course en 0,15\text{~h}. Qui a gagné la course ?


La course s'effectue en 7 tours de piste.
1. Calculer le périmètre de la piste, puis la distance parcourue par les chevaux. On arrondira au mètre près.
| Tour | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Durée | 51 \text{~s} | 1\text{~min~} 12 \text{~s} | 1 \text{~min~} 24 \text{~s} | 1 \text{~min~} 48 \text{~s} | 59\text{~s} | 1\text{~min~} 26 \text{~s} | 2 \text{~min} |
Calculer astucieusement la durée totale de la course de Marcus.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Solides, pensée algébrique, probabilités
Esteban possède 100 cubes numérotés de 1 à 100.
1. Il pioche un premier cube au hasard. Quelle est la probabilité que le nombre de ce cube comporte au moins un zéro ?
1. Il pioche un premier cube au hasard. Quelle est la probabilité que le nombre de ce cube comporte au moins un zéro ?
2. Il décide d'assembler ses cubes en ajoutant à chaque étape un cube devant, un cube au-dessus et un cube à droite.

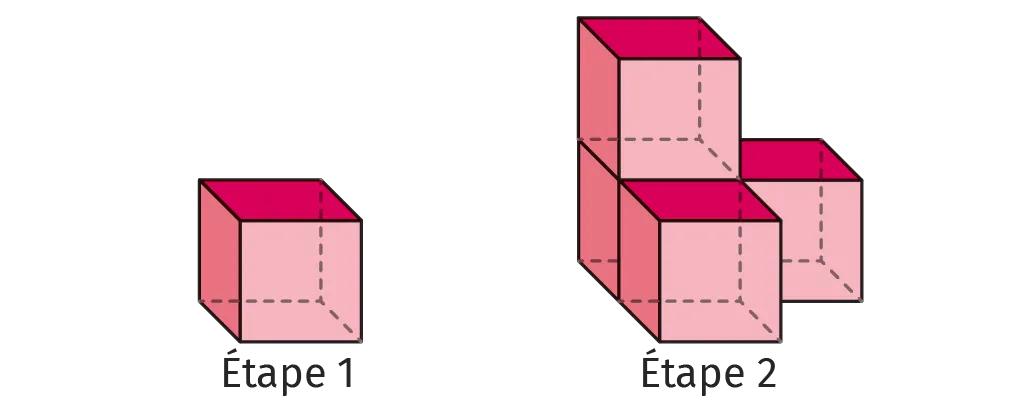
a. Dessiner à main levée la vue du dessus obtenue à l'étape 2.


a. Dessiner à main levée la vue du dessus obtenue à l'étape 2.
Cliquez ici pour avoir accès à un espace de dessin
b. Combien de cubes doit-il utiliser pour réaliser l'étape 3 ?
c. Avec ses 100 cubes, jusqu'à quelle étape peut-il aller ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Entiers, durées, aires et périmètres
Dessiner un monstre dont les différentes parties du corps sont à découvrir en répondant aux énoncés ci-dessous.
Cliquez ici pour avoir accès à un espace de dessin
| Énoncé | Cocher la bonne réponse. | ||
|---|---|---|---|
| Le corps et la tête | Calculer l'aire d'un carré de côté 4,5~\mathrm{cm}. | ||
| Les jambes et les pieds | Déterminer le nombre de centaines de millions dans 12~451~125~259. | ||
| Les oreilles | Convertir 3,4~\mathrm{h} en heures et minutes. | ||
| Les bras | Convertir 25,412~\mathrm{m}^2 en \mathrm{cm}^2. | ||
| Les yeux | Déterminer le plus grand nombre parmi \pi et 3,2. | ||
| La bouche et le nez | Calculer la valeur approchée au centimètre du périmètre d'un cercle de diamètre 5~\mathrm{cm}. | ||
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Cercles et disques, médiatrice, symétrie axiale, algorithmique
Une aventurière a enfoui un trésor dans une grotte de l'île dont on donne la carte ci-dessous. Sur cette carte, le point \mathrm{B} représente le bateau et le point \mathrm{T} représente un tunnel. Elle a rédigé des indices lui permettant de retrouver son trésor.
1. Tracer le cercle de centre \mathrm{B} et de rayon 50~\mathrm{m}. Placer la source d'eau potable \mathrm{E} à l'intersection de la droite (d) et de ce cercle.
2. Placer la cabane \mathrm{C}, symétrique du tunnel \mathrm{T} par rapport à la droite (d).
3. Un vieil arbre \mathrm{A} se situe au milieu du segment [\mathrm{EC}]. Placer \mathrm{A} sur la carte. \mathrm{A} doit être situé à l'intersection de carreaux.
4. Afin d'éviter les falaises, partir du vieil arbre \mathrm{A}, marcher 20~\mathrm{m} vers le sud, 30~\mathrm{m} vers l'ouest, 20~\mathrm{m} vers le nord, 10~\mathrm{m} vers l'ouest et 10~\mathrm{m} vers le nord. On atteint un lac asséché, repéré par le point \mathrm{L}. Placer \mathrm{L} sur la carte.
5. Tracer la médiatrice de [\mathrm{CL}]. Elle coupe la droite (\mathrm{AB}) en \mathrm{G}, la grotte. Placer \mathrm{G} sur la carte.
1. Tracer le cercle de centre \mathrm{B} et de rayon 50~\mathrm{m}. Placer la source d'eau potable \mathrm{E} à l'intersection de la droite (d) et de ce cercle.
2. Placer la cabane \mathrm{C}, symétrique du tunnel \mathrm{T} par rapport à la droite (d).
3. Un vieil arbre \mathrm{A} se situe au milieu du segment [\mathrm{EC}]. Placer \mathrm{A} sur la carte. \mathrm{A} doit être situé à l'intersection de carreaux.
4. Afin d'éviter les falaises, partir du vieil arbre \mathrm{A}, marcher 20~\mathrm{m} vers le sud, 30~\mathrm{m} vers l'ouest, 20~\mathrm{m} vers le nord, 10~\mathrm{m} vers l'ouest et 10~\mathrm{m} vers le nord. On atteint un lac asséché, repéré par le point \mathrm{L}. Placer \mathrm{L} sur la carte.
5. Tracer la médiatrice de [\mathrm{CL}]. Elle coupe la droite (\mathrm{AB}) en \mathrm{G}, la grotte. Placer \mathrm{G} sur la carte.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9Fractions, pourcentages, aires
Un promoteur immobilier achète un terrain afin de construire un immeuble avec des aménagements extérieurs.
1. Un jardin potager partagé occupera 8~\% de la superficie totale, le parking \frac{3}{5} et l'aire de jeux \frac{1}{8}.
a. Écrire ces trois nombres sous la forme de fractions dont le dénominateur vaut 200.
b. Classer ces trois aménagements extérieurs dans l'ordre croissant de leur superficie.
c. Quelle proportion de la superficie totale reste-t-il ?
2. Le terrain est représenté ci-dessous. Quelle est sa superficie, exprimée en \mathrm{m}^2 ?

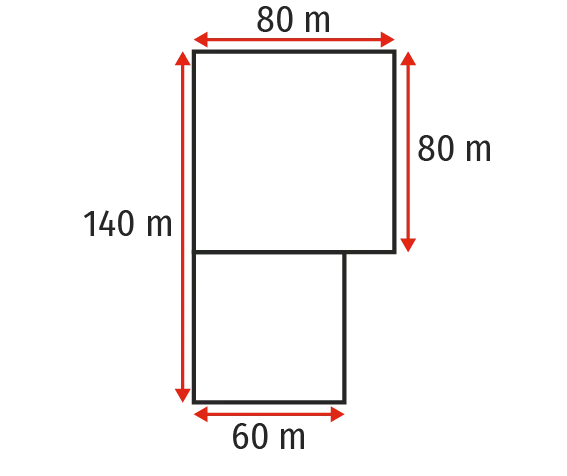 3. a. Déterminer la surface occupée par chaque aménagement extérieur.
b. L'immeuble va occuper 1~550 \mathrm{m}^2. En déduire l'aire du jardin paysager qui occupe l'espace restant.
3. a. Déterminer la surface occupée par chaque aménagement extérieur.
b. L'immeuble va occuper 1~550 \mathrm{m}^2. En déduire l'aire du jardin paysager qui occupe l'espace restant.
1. Un jardin potager partagé occupera 8~\% de la superficie totale, le parking \frac{3}{5} et l'aire de jeux \frac{1}{8}.
a. Écrire ces trois nombres sous la forme de fractions dont le dénominateur vaut 200.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10Décimaux, alignement de points, triangles et angles
On donne la figure ci-dessous. La figure n'est pas à l'échelle.

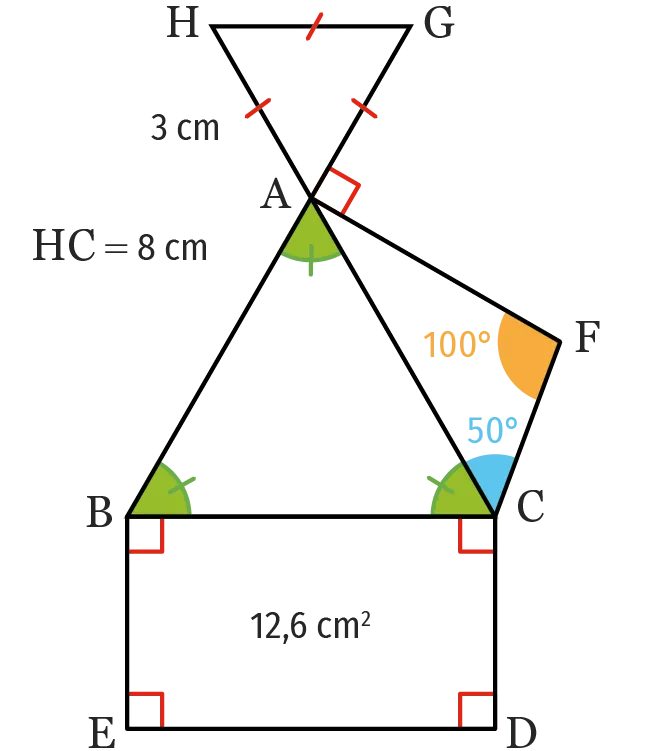
1. a. Montrer que \widehat{\mathrm{H}\mathrm{A}\mathrm{C}} = 180°. Que peut-on en déduire sur les points \mathrm{H}, \mathrm{A} et \mathrm{C} ?
b. En déduire la longueur \mathrm{A}\mathrm{C}.
c. Quelles sont les dimensions du triangle \mathrm{A}\mathrm{B}\mathrm{C} ?
2. Déterminer, en posant le calcul, la longueur \mathrm{B}\mathrm{E}.


1. a. Montrer que \widehat{\mathrm{H}\mathrm{A}\mathrm{C}} = 180°. Que peut-on en déduire sur les points \mathrm{H}, \mathrm{A} et \mathrm{C} ?
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11 Aire, décimaux
On donne ci-dessous les dimensions de deux équerres en plastique vendues dans le commerce. On suppose les deux équerres de même épaisseur.
1. Coder les angles droits sur les figures.
2. Réaliser un schéma dans lequel les triangles \mathrm{ABC}, \mathrm{DEF} et \mathrm{GHI} sont chacun obtenus en coupant un rectangle en deux surfaces égales. Indiquer les mesures de ces rectangles sur le schéma.
Schéma 1
Schéma 2
Schéma 3
3. Calculer l'aire de chacun de ces rectangles en posant les opérations de multiplication.
4. En déduire les aires des différents triangles. On posera les opérations.
5. Laquelle de ces équerres nécessite le moins de plastique ?
2. Réaliser un schéma dans lequel les triangles \mathrm{ABC}, \mathrm{DEF} et \mathrm{GHI} sont chacun obtenus en coupant un rectangle en deux surfaces égales. Indiquer les mesures de ces rectangles sur le schéma.
Schéma 1
Cliquez ici pour avoir accès à un espace de dessin
Cliquez ici pour avoir accès à un espace de dessin
Cliquez ici pour avoir accès à un espace de dessin
3. Calculer l'aire de chacun de ces rectangles en posant les opérations de multiplication.
Cliquez ici pour avoir accès à un espace de dessin
Cliquez ici pour avoir accès à un espace de dessin
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

