Sommaire
Mes pages
N° Page
Ouverture
p. 1-10
Algorithmique et programmation
Partie 1 : Nombres et calculs
Partie 2 : Organisation et gestion de données, fonctions
Partie 3 : Espace et géométrie
Prolongement
Vers la troisième
Exercicesp. 290-296
Réviser avec Genially
Genially
Nos dossiers d'actualités
Dossier d'actualité
/ 296
Page précédente
Chapitre 14
Exercices d'entraînement

2 - Cônes de révolution

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Vérifier que les connaissances de base sont acquises.
Développer les connaissances.
Maîtriser les notions de manière approfondie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

54
[Com.1 - Ch.2]

Créer une grille de mots croisés accompagnée de définitions à partir des mots suivants. Une grille peut être téléchargée
ici
.

1. Cône

2. Volume

3. Hauteur

4. Génératrice
5. Rayon

6. Base

7. Sommet

Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

55
[Rep.7 - Com.1]

Soit \text{DOG} un triangle rectangle en \text{D}. Dans chacun des deux cas suivants donner :
  • le sommet du cône de révolution ;
  • le rayon de la base ;
  • la hauteur et la génératrice ;
  • une représentation en perspective cavalière.
1. Le cône est engendré par la rotation du triangle autour de la droite (\mathrm{DO}).

Cliquez pour accéder à une zone de dessin

2. Le cône est engendré par la rotation du triangle autour de la droite (\mathrm{DG}).

Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

56
[Cal.2 - Ch.1 - Rep.5]

Donner le volume exact des cônes de révolution suivants sous la forme d'une fraction puis les classer dans l'ordre croissant de leur volume.
1.
Figure d'un cône de révolution

2.
Figure d'un cône de révolution

3.
Figure d'un cône de révolution
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

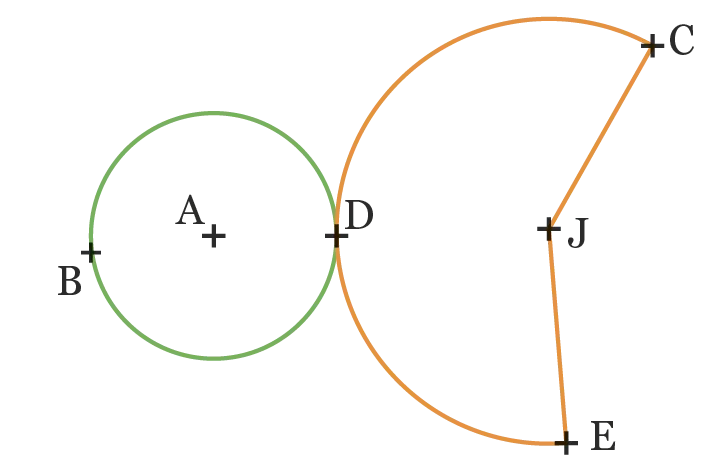
57
[Mod.4 - Cal.5]

On considère le patron du cône de révolution suivant. Sachant que la longueur de l'arc de cercle \overgroup{\mathrm{CE}} du secteur orange est de \text{18,3~cm}, calculer la longueur du rayon [\mathrm{AB}] du cercle vert, puis l'aire du disque de base de ce cône arrondie au dixième près.
Placeholder pour Diagramme : deux cercles tangents, points (A, B, C, D, E, J) et lignes nommés.Diagramme : deux cercles tangents, points (A, B, C, D, E, J) et lignes nommés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

58
[Cal.5 - Ch.1 - Com.3]

Lisa effectue le pochage de petits gâteaux à l'aide d'une poche à douille assimilable à un cône de révolution. Ce cône a pour diamètre \text{12~cm} et pour hauteur \text{21~cm}. Sachant qu'il faut \text{2~cL} de crème pour chaque gâteau, combien de gâteaux complets pourra-t-elle faire ?
Coup de pouce
1 \mathrm{~mL}=1 \mathrm{~cm}^{3}
Placeholder pour Photo : pâtissière décorant des cupcakes avec une poche à douille, crème bleu pâle en rosaces.Photo : pâtissière décorant des cupcakes avec une poche à douille, crème bleu pâle en rosaces.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

59
[Rep.3 - Rep.6 - Mod.3]

On souhaite construire le patron du cône suivant.
Illustration d'un cône et son patron
1. Exprimer en fonction de \pi la longueur \mathrm{L}_{1} du cercle de base et la longueur \mathrm{L}_{2} d'un disque de rayon \text{6~cm}. Donner la valeur exacte.

2. On cherche à déterminer la mesure de l'angle \widehat{\mathrm{CBC}^{\prime}} permettant de tracer le secteur correspondant à la face latérale du cône. Pour cela, compléter le tableau de proportionnalité suivant.
Secteur de la face latéraleDisque entier
Longueur de l'arc\mathrm{L}_{1}=
\mathrm{L}_{2}=
Angle en { }^{\circ}
360

2. Tracer ce patron en vraie grandeur.

Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

60
[Rep.3 - Rep.6 - Mod.3]

Tracer en grandeur réelle un patron d'un cône de révolution tel que :
  • la génératrice mesure \text{8,5~cm} ;
  • le diamètre de la base est \text{10~cm}.
On arrondira les valeurs calculées à l'unité près pour réaliser la figure.

Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

61
Environnement et développement durable
[Rais.3 - Ch.1 - Cal.2]


Afin d'économiser de l'eau, M. Martin veut acheter un récupérateur d'eau pour arroser son potager.
Il a besoin de trois arrosoirs de six litres remplis aux trois quarts par arrosage.
Il arrose tous les deux jours.
Dans le magasin de jardinage, un vendeur lui propose un modèle en forme de cône de diamètre \text{60~cm} et de hauteur \text{121~cm}.
Image d'un potager de tomate avec un récupérateur d'eau en forme de cône
1. Quelle est la capacité, en litre, du récupérateur d'eau ?
2. Si le récupérateur d'eau est plein, au bout de combien de jours sera-t-il vide en supposant qu'il ne pleuve pas entre-temps ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

62
[Cal.2 - Cal.5]

Soit \text{CAT} un triangle rectangle en \text{A} tel que \text{CA = 5~cm} et \text{AT = 7~cm}.

1. Quel est le volume \mathrm{V}_{1} du cône de révolution généré par la rotation de \text{CAT} autour de la droite (\mathrm{AT}) ?

2. Quel est le volume \mathrm{V}_{2} du cône de révolution généré par la rotation de \text{CAT} autour de la droite (\mathrm{CA}) ?

3. Comparer les quotients \frac{\mathrm{V}_{1}}{\mathrm{~V}_{2}} et \frac{\mathrm{CA}}{\mathrm{AT}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

63
Inversé
[Ch.2 - Ch.4]

Le secteur angulaire d'un patron de cône possède un angle de \text{150°}. Trouver la longueur d'un diamètre et d'une génératrice de ce cône afin d'obtenir cet angle.
Page suivante

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille