Prolongement
Exercices d'entraînement
Vers la troisième
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
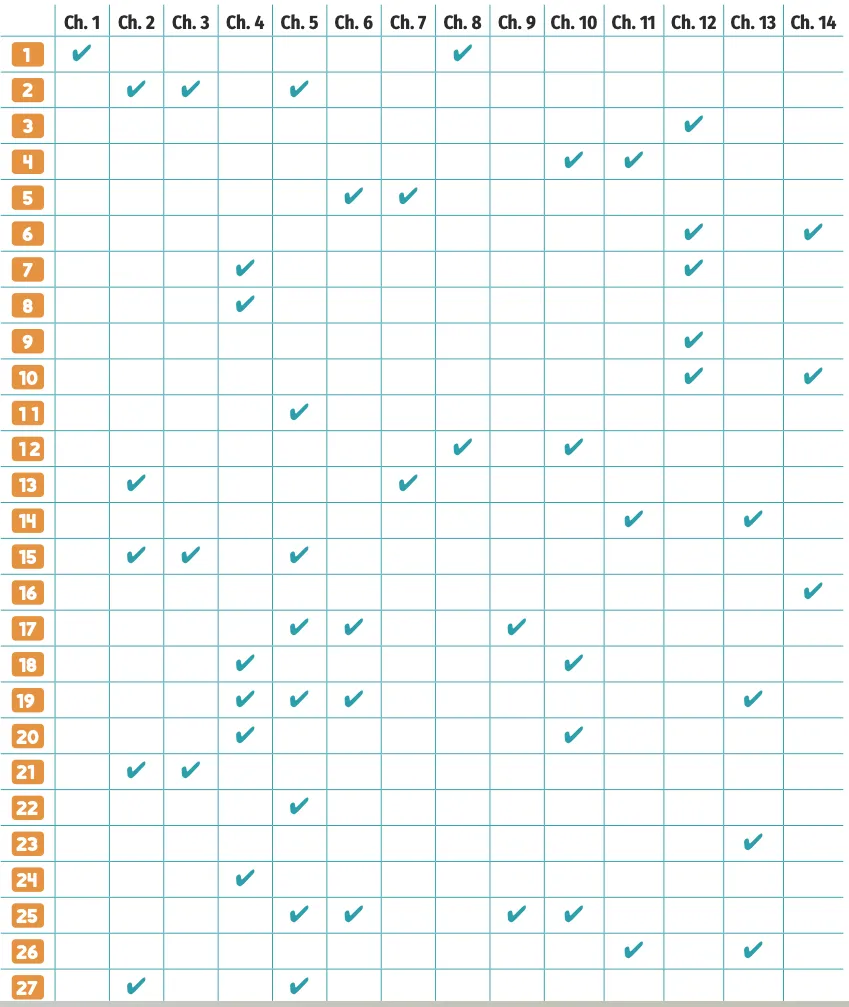
Chapitres utilisés dans ces exercices
Les pages suivantes permettent aux élèves de se préparer à la classe de troisième en proposant des exercices variés. Certains de ces exercices utilisent des notions de plusieurs chapitres.
Le tableau suivant indique les chapitres concernés pour chaque exercice.



Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Chapitres et
On place dans une urne les six papiers
suivants.

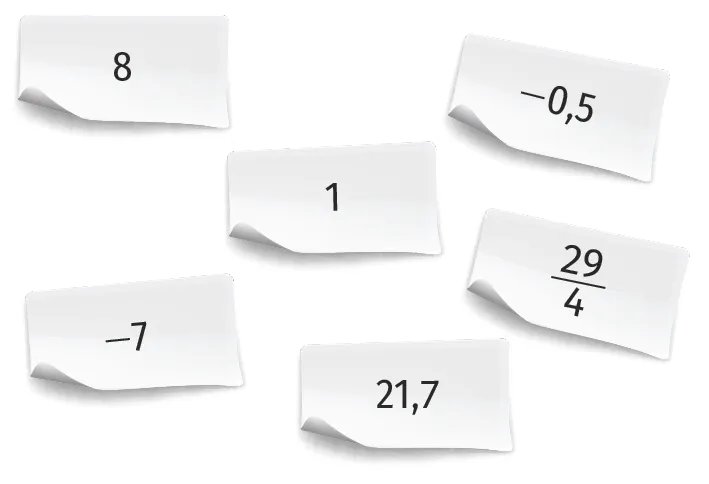 Geoffrey pioche deux papiers, l'un après l'autre, au hasard dans cette urne.
Geoffrey pioche deux papiers, l'un après l'autre, au hasard dans cette urne.

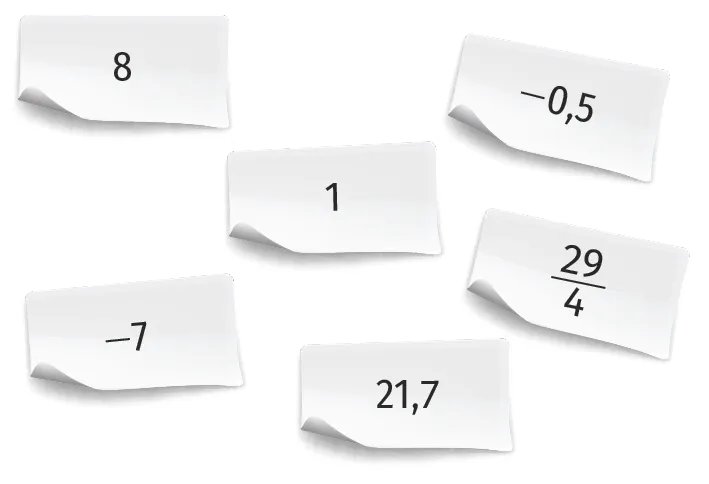
1. Quelle est la probabilité qu'il obtienne deux nombres dont la somme est égale à \text{0} ?
2. On suppose que le premier papier pioché par Geoffrey est le nombre -7.
a. Combien de papiers reste-t-il ?
b. Parmi ces papiers restants, il en pioche un au hasard. Quelle est la probabilité que le produit de -7 par ce nombre soit positif ? Négatif ?
3. Quelle est la probabilité que la somme de ce nombre et -7 soit positive ?
2. On suppose que le premier papier pioché par Geoffrey est le nombre -7.
a. Combien de papiers reste-t-il ?
b. Parmi ces papiers restants, il en pioche un au hasard. Quelle est la probabilité que le produit de -7 par ce nombre soit positif ? Négatif ?
3. Quelle est la probabilité que la somme de ce nombre et -7 soit positive ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Chapitres , et
Soit x un nombre. Dans cet exercice, on s'intéresse à l'expression \mathrm{A}=\frac{1}{\frac{9}{8} \times x+\frac{3}{4}}.
1. a. Quelle est la valeur de \text{A} lorsque x=\frac{2}{3} ?
b. Quelle est la valeur de \text{A} lorsque x=\frac{1}{\frac{9}{8} \times \frac{2}{3}+\frac{3}{4}} ?
2. Sans effectuer de calcul, déterminer la valeur de l'expression \text{B}=~\frac{1}{\frac{9}{8} \times \frac{1}{\frac{9}{8} \times \frac{1}{\frac{9}{8} \times \frac{2}{3}+\frac{3}{4}}+\frac{3}{4}}+\frac{3}{4}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Chapitre
1. a. Tracer un carré \text{ABCD} de côté
8 carreaux.

2. a. Tracer un triangle \text{FGH} rectangle en \text{F} et de dimensions quelconques.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Chapitres et
\text{ABC} est un triangle. \text{M} est un point de [\mathrm{AB}] et \text{N} est un point de [\mathrm{AC}] tels que (\mathrm{MN}) est parallèle à (\mathrm{BC}). De plus, on sait que \text{AN = 12~cm} et \text{NC = 6~cm}.1. Faire un schéma.
3. a. Que vaut la longueur \text{MN} si \text{BC = 5~cm} ?
b. Compléter le tableau ci-dessous.
| \text{BC} (en cm) | \text{1} | \text{2} | \text{3} | \text{4} | \text{5} |
|---|---|---|---|---|---|
| \text{MN} (en cm) |
4. Que peut-on dire des longueurs \text{BC} et \text{MN} ? Pouvait‑on le prévoir ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Chapitres et
Isabelle tient un stand de chamboule‑tout dans une kermesse. Elle a
en sa possession 20 canettes cylindriques dont l'aire de la base
est \text{15,5~cm}2 et la hauteur de \text{8~cm}. Elle souhaite les empiler comme ci-contre.
Sachant que le support sur lequel elle doit poser cet empilement est un carré de côté \text{220~mm}, combien de boîtes de conserve pourra-t-elle utiliser au maximum pour ce chamboule-tout ? Quel sera alors la hauteur de cet empilement ?
Sachant que le support sur lequel elle doit poser cet empilement est un carré de côté \text{220~mm}, combien de boîtes de conserve pourra-t-elle utiliser au maximum pour ce chamboule-tout ? Quel sera alors la hauteur de cet empilement ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Chapitres et
Les nombres \text{1 = 2}0, \text{2 = 2}1, \text{4 = 2}2, \text{8 = 2}3, etc. sont appelés puissances de \text{2}.
Dans cet exercice, on s'intéresse aux triangles rectangles ci-dessous.

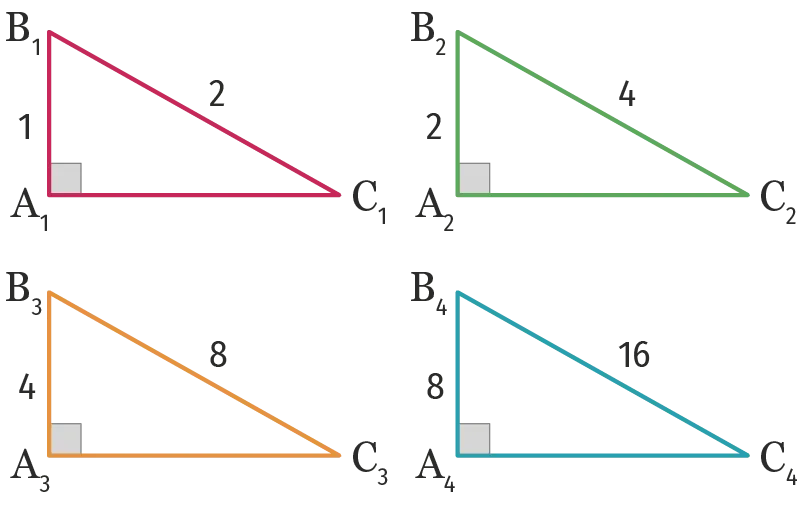
Dans cet exercice, on s'intéresse aux triangles rectangles ci-dessous.


1. a. Conjecturer la méthode de construction de ces triangles.
b. En suivant la même logique de construction, déterminer la longueur de l'hypoténuse du triangle \text{A}_{5} \text{B}_{5} \text{C}_{5}.
2. a. Combien mesure l'angle \widehat{\mathrm{A}_{1} \mathrm{B}_{1} \mathrm{C}_{1}} ? Justifier.
b. Combien mesure l'angle \widehat{\mathrm{A}_{2} \mathrm{B}_{2} \mathrm{C}_{2}} ? Justifier.
c. Quelle conjecture peut-on faire concernant les angles \widehat{\mathrm{A}_{3} \mathrm{B}_{3} \mathrm{C}_{3}}, \widehat{\mathrm{A}_{4} \mathrm{B}_{4} \mathrm{C}_{4}}, etc. ?
b. En suivant la même logique de construction, déterminer la longueur de l'hypoténuse du triangle \text{A}_{5} \text{B}_{5} \text{C}_{5}.
2. a. Combien mesure l'angle \widehat{\mathrm{A}_{1} \mathrm{B}_{1} \mathrm{C}_{1}} ? Justifier.
b. Combien mesure l'angle \widehat{\mathrm{A}_{2} \mathrm{B}_{2} \mathrm{C}_{2}} ? Justifier.
c. Quelle conjecture peut-on faire concernant les angles \widehat{\mathrm{A}_{3} \mathrm{B}_{3} \mathrm{C}_{3}}, \widehat{\mathrm{A}_{4} \mathrm{B}_{4} \mathrm{C}_{4}}, etc. ?
3. Dans les questions suivantes, les valeurs exactes sont attendues.
a. Calculer la longueur \mathrm{A}_{1} \mathrm{C}_{1}.
b. Calculer la longueur \mathrm{A}_{2} \mathrm{C}_{2}.
c. Calculer la longueur \mathrm{A}_{3} \mathrm{C}_{3}.
d. Sans utiliser le théorème de Pythagore, conjecturer la longueur du segment \left[\mathrm{A}_{4} \mathrm{C}_{4}\right] puis du segment \left[\mathrm{A}_{8} \mathrm{C}_{8}\right].
a. Calculer la longueur \mathrm{A}_{1} \mathrm{C}_{1}.
b. Calculer la longueur \mathrm{A}_{2} \mathrm{C}_{2}.
c. Calculer la longueur \mathrm{A}_{3} \mathrm{C}_{3}.
d. Sans utiliser le théorème de Pythagore, conjecturer la longueur du segment \left[\mathrm{A}_{4} \mathrm{C}_{4}\right] puis du segment \left[\mathrm{A}_{8} \mathrm{C}_{8}\right].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Chapitre
Je suis un nombre entier.
Mon carré est compris entre \text{140} et \text{200}. Ma racine carrée est inférieure à \text{3,5}.
Qui suis‑je ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9Chapitre
1. Tracer un quadrilatère \text{ABCD} quelconque dont les côtés ne se croisent pas.
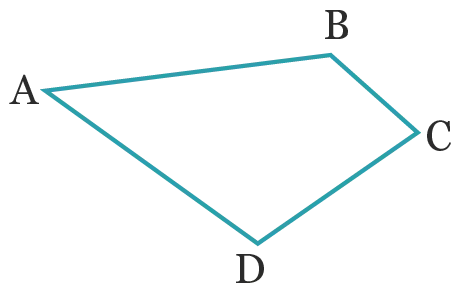
2. Déterminer la valeur de \widehat{\mathrm{ABC}}+\widehat{\mathrm{BCD}}+\widehat{\mathrm{CDA}}+\widehat{\mathrm{DAB}}.
3. On suppose maintenant que \widehat{\mathrm{DAB}}=\widehat{\mathrm{ABC}}=90^{\circ}, que \widehat{\mathrm{BCD}}=110^{\circ} et que \mathrm{AB}~=~8 \mathrm{~cm} et \mathrm{BD}~=~10 \mathrm{~cm}.
a. Calculer la mesure de l'angle \widehat{\mathrm{ADC}}.
b. Calculer les mesures des angles du triangle \text{BCD}, arrondies au dixième près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10Chapitres et
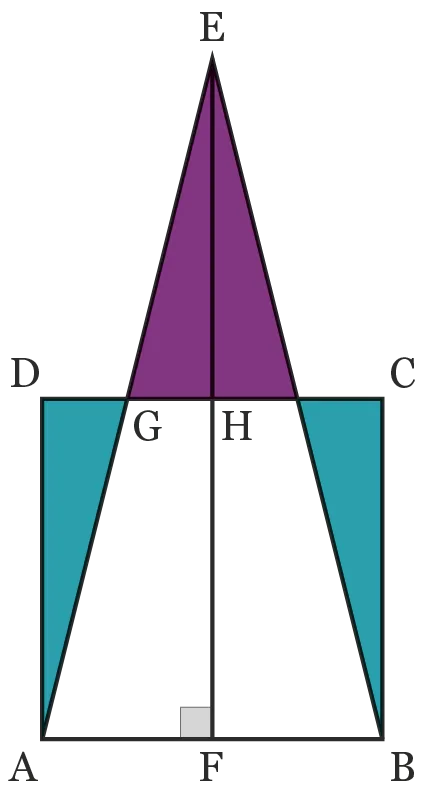
On considère la pyramide \text{ABCDE} à base carrée suivante.
L'objectif est de calculer son volume.

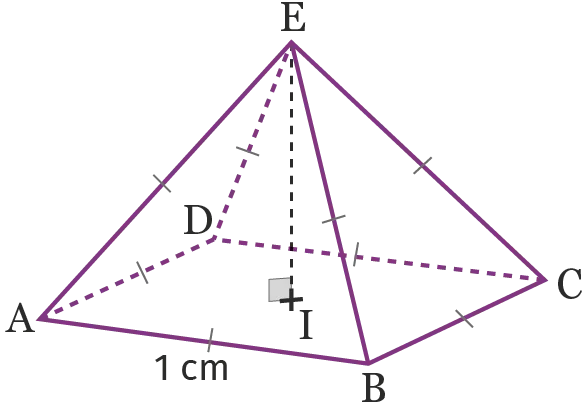
L'objectif est de calculer son volume.


1. Déterminer l'aire du carré \text{ABCD}.
2. a. Quelle est la nature du triangle \text{ABD} ?
b. Calculer la longueur \text{BD} et arrondir le résultat au centième.
2. a. Quelle est la nature du triangle \text{ABD} ?
b. Calculer la longueur \text{BD} et arrondir le résultat au centième.
3. On note \text{I} le pied de la hauteur issue de \text{E} dans le triangle \text{BDE}. On admet que \text{I} est le milieu de [\mathrm{BD}] et que [\mathrm{EI}] est la hauteur de la pyramide.
a. Quelle est la nature du triangle \text{BIE} ?
b. Calculer la longueur \text{IE} arrondie au centième près.
4. Calculer alors le volume de la pyramide arrondi à \text{0,01~cm}3 près.
a. Quelle est la nature du triangle \text{BIE} ?
b. Calculer la longueur \text{IE} arrondie au centième près.
4. Calculer alors le volume de la pyramide arrondi à \text{0,01~cm}3 près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11Chapitre
Soit x un nombre strictement positif. Reproduire et compléter les schémas suivants de manière à ce que toutes les figures représentées aient pour périmètre \mathrm{x~cm}.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12Chapitres et
Pour remplir la deuxième colonne du tableau suivant, Drishti décide de lancer deux dés équilibrés à six faces. La première ligne
du tableau ci-dessous est complétée avec
le résultat du premier dé et la deuxième ligne avec celui du deuxième dé. Drishti se demande quelle la probabilité qu'il obtienne ainsi un tableau de proportionnalité.| x | 7 | ? |
|---|---|---|
| y | 3,5 | ? |
1. Dans le tableau suivant, cocher les cases permettant d'obtenir un tableau de proportionnalité.
| \text{Dé}~1 \to \text{Dé}~2 \downarrow | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 |
2. En déduire alors la probabilité que Drishti obtienne un tableau de proportionnalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13Chapitres et
Olivier, employé d'un institut de sondage, est chargé de créer un diagramme circulaire récapitulant les réponses obtenues à la question « De quelle couleur est votre voiture ? ».
Malheureusement, un bug dans le système a détruit une grande majorité des données de ce sondage. Il ne lui reste plus que les informations suivantes.
- Les participants ne pouvaient répondre que bleue, rouge, grise ou noire à cette question.
- Les sondés ont répondu grise ou noire avec une fréquence de \frac{5}{16}.
- Les sondés ont répondu bleue ou rouge avec une fréquence de \frac{11}{16}.
- Les sondés ont répondu rouge ou grise avec une fréquence de \frac{23}{48}.
- \frac{7}{48} des sondés ont r�épondu que leur voiture était noire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15Chapitres , et
Les propositions ci-dessous sont-elles
vraies ou fausses ? Justifier.
1. La somme de deux nombres rationnels peut être égale à \text{0}.
2. Un nombre rationnel et son inverse sont toujours différents.
2. Un nombre rationnel et son inverse sont toujours différents.
3. On peut trouver des nombres entiers a et b tels que \frac{a}{3} \times \frac{b}{4}=\frac{1}{2}.
4. On peut trouver des nombres entiers a et b tels que \frac{a}{3}+\frac{b}{4}=\frac{1}{2}.
4. On peut trouver des nombres entiers a et b tels que \frac{a}{3}+\frac{b}{4}=\frac{1}{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16Chapitre
Au bar dans lequel elle travaille, Flora possède
des verres de trois formes différentes :
- conique de hauteur \text{18~cm} dont le pied mesure \text{9~cm} et dont l'aire de la base est \text{35 cm}2 ;
- cylindrique de hauteur \text{10~cm} et de base d'aire \text{40~cm}2 ;
- en forme de pavé droit de longueur \text{3~cm}, de largeur \text{2~cm} et de hauteur \text{6~cm}.

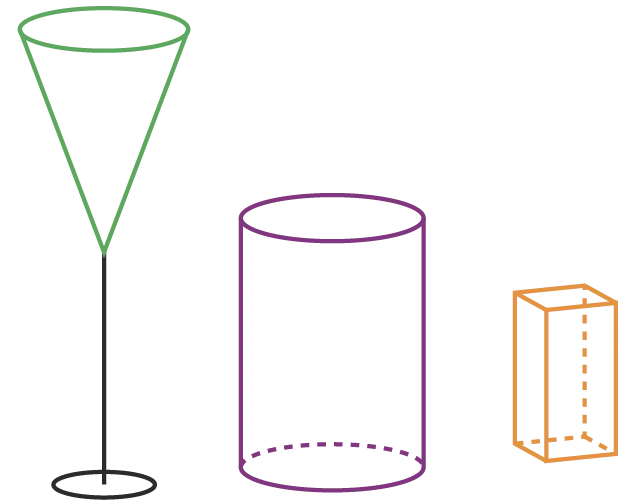
Munie d'une bouteille d'eau, Flora remplit tout d'abord un verre cylindrique à ras bord avant de verser son contenu dans un verre conique jusqu'à ce que ce dernier soit plein. Enfin, elle verse le contenu du verre conique jusqu'à remplir totalement un verre en forme de pavé droit.
À la fin de cette procédure, quel volume d'eau est contenu dans chacun des verres ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17Chapitres , et
On considère la fonction f définie pour
tout nombre x par la formule {3x - 5}.1. Compléter le tableau de valeurs suivant.
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| 3 x-5 |
2. a. La fonction f est représentée par une droite. Tracer cette droite dans un repère en prenant 1 carreau comme unité sur les deux axes.
c. Lire graphiquement le nombre en abscisse auquel on associe le nombre \text{4} en ordonnée.
3. a. Lorsque x = -3,2, calculer la valeur de la fonction f.
b. Calculer la valeur du nombre auquel on associe le nombre -11.
c. La droite représentant f coupe l'axe des abscisses en un point. Calculer les coordonnées exactes de ce point.
4. Placer de façon exacte le nombre \frac{1}{3} sur l'axe des abscisses.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18Chapitres et
L'atome d'hydrogène est assimilé à une sphère de diamètre \text{0,106~nm}. L'atome de carbone est assimilé à une sphère de diamètre \text{0,124~nm}.
1. Que signifie l'unité \text{nm} ?
2. Convertir les deux diamètres en mètre en donnant la notation scientifique du résultat.
1. Que signifie l'unité \text{nm} ?
2. Convertir les deux diamètres en mètre en donnant la notation scientifique du résultat.
3. Justifier que l'atome de carbone est approximativement \text{1,17} fois plus gros que celui d'hydrogène.
4. Dans une boîte de jeu permettant de reconstituer des molécules à partir d'atomes, l'atome d'hydrogène a un diamètre de \text{17~mm} et celui de carbone a un diamètre de \text{23~mm}. La proportion des deux atomes est-elle respectée ? Justifier.
4. Dans une boîte de jeu permettant de reconstituer des molécules à partir d'atomes, l'atome d'hydrogène a un diamètre de \text{17~mm} et celui de carbone a un diamètre de \text{23~mm}. La proportion des deux atomes est-elle respectée ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19Chapitres , , et
L'ancien drapeau de la République du Congo est un rectangle dont on donne les proportions à respecter pour le représenter correctement.

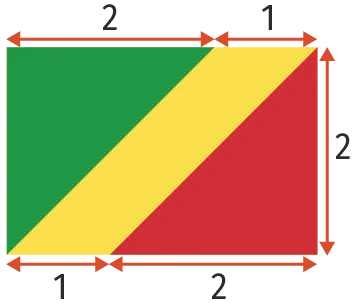


1. Que peut-on dire des triangles rectangles vert et rouge apparaissant sur le drapeau ?
2. Démontrer que la bande jaune a la même aire que le triangle vert.
3. Jasmine veut coudre un drapeau identifque de façon à ce que l'aire de la bande jaune soit égale à \text{8~m}2. Quelles seront la longueur et la largeur du drapeau que Jasmine va devoir réaliser ?
2. Démontrer que la bande jaune a la même aire que le triangle vert.
3. Jasmine veut coudre un drapeau identifque de façon à ce que l'aire de la bande jaune soit égale à \text{8~m}2. Quelles seront la longueur et la largeur du drapeau que Jasmine va devoir réaliser ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20Chapitres et
Une voiture roule à une vitesse moyenne
de \text{100~km/h}. Un être humain vit \text{100} ans.
La distance entre la Terre et Saturne est de l'ordre de \text{10}^{9}\text{~km}.
Si une route était construite entre la Terre et Saturne, combien d'humains devraient se succéder au volant d'une voiture pour se rendre sur cette planète ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21Chapitres et
1. Compléter la grille ci-dessous avec des nombres rationnels de manière à ce que les sommes des nombres de chaque ligne et de chaque colonne soient égales.| \frac{1}{2} | \frac{1}{3} | \frac{1}{4} |
| \frac{1}{20} | ||
| \frac{23}{60} |
2. Compléter cette même grille mais cette fois‑ci les produits des nombres de chaque ligne et de chaque colonne doivent être égaux.
| \frac{1}{2} | \frac{1}{3} | \frac{1}{4} |
| \frac{1}{20} | ||
| \frac{23}{60} |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22Chapitre
Soit x un nombre strictement supérieur à \text{1}. On considère le rectangle suivant de longueur x+1 et de largeur x-1.


2. On colorie dans ce rectangle un rectangle en rouge de largeur \text{1}, comme indiqué.


3. On découpe ce rectangle rouge avant de le coller comme indiqué. Déterminer les valeurs manquantes sur la figure 2.

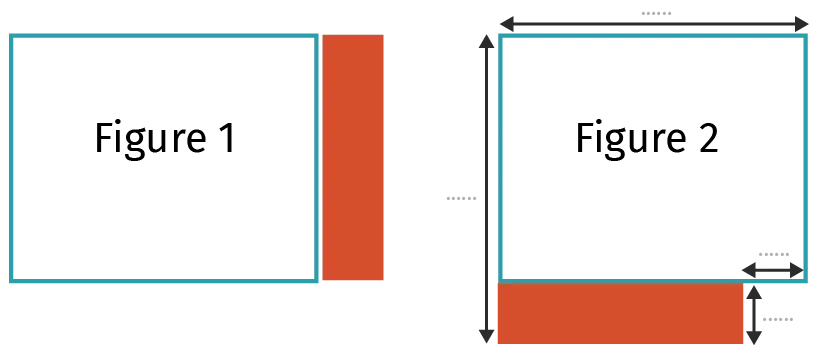
4. Justifier que l'aire de la figure 2 est égale à x^{2}~-~1.
5. En découpant ce rectangle rouge et en le déplaçant, a-t-on modifié l'aire de la figure initiale ? Que peut-on donc dire de (x+1)(x-1) et de {x^{2}-1} ?
6. Sans calculatrice et sans poser de calcul, déterminer le résultat du produit 101 \times 99.
7. En utilisant le résultat de la question 5, résoudre l'équation {(x+1)(x-1)=24}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23Chapitre
TikTok est une application mobile de partage de vidéos développée par l'entreprise chinoise ByteDance. Son logo représente trois notes, de trois couleurs différentes, superposées.


1. Exécuter le programme de construction suivant.
2. Que peut-on dire des droites (\mathrm{BE}) et (\mathrm{AB}) ? Justifier.
3. Quel type de transformation du plan pourrait-on utiliser pour obtenir la note bleue et la note rouge à partir de la note noire que l'on vient de dessiner ?
- Sur une feuille de papier, tracer un cercle \mathcal{C} de centre \text{O}.
- Tracer un diamètre [\mathrm{AB}] de ce cercle, \text{A} devant se trouver du « côté gauche du cercle » puis un autre diamètre [\mathrm{CD}]de \mathcal{C} tel que (\mathrm{AB}) et (\mathrm{CD}) soient perpendiculaires. On placera \text{C} « en bas du cercle ».
- Placer \text{E} l'image de \text{B} par la translation transformant \text{C} en \text{D}.
- Tracer le segment [\mathrm{BE}].
- Tracer l'image du quart de cercle \overgroup{\mathrm{AC}} par la translation transformant \text{A} en \text{E}.
- Effacer le quart de cercle \overgroup{\mathrm{DB}}.
3. Quel type de transformation du plan pourrait-on utiliser pour obtenir la note bleue et la note rouge à partir de la note noire que l'on vient de dessiner ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24Chapitre
On colorie un carré de la façon suivante.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Chapitres , , et
D'après Brevet, Polynésie, 2020
Farid et Gwenaëlle décident tous les deux de partir en randonnée et de suivre le même parcours. Farid part 45 minutes avant Gwenaëlle. De plus, il marche à une vitesse constante de \text{4~km/h} tandis que Gwenaëlle marche à une vitesse constante de \text{6~km/h}.
1. Au moment du départ de Gwenaëlle, quelle est la distance déjà parcourue par Farid ?
On note t le temps écoulé, exprimé en heure, depuis le départ de Gwenaëlle. Ainsi, t = 0 correspond au moment du départ de Gwenaëlle.
2. Soit g la fonction exprimant la distance parcourue par Gwenaëlle en fonction de t. Donner l'expression de cette fonction g.
3. Expliquer pourquoi la distance en kilomètre parcourue par Farid en fonction de t peut s'écrire 4 t+3. On appelle désormais cette fonction f.
Farid et Gwenaëlle décident tous les deux de partir en randonnée et de suivre le même parcours. Farid part 45 minutes avant Gwenaëlle. De plus, il marche à une vitesse constante de \text{4~km/h} tandis que Gwenaëlle marche à une vitesse constante de \text{6~km/h}.
1. Au moment du départ de Gwenaëlle, quelle est la distance déjà parcourue par Farid ?
On note t le temps écoulé, exprimé en heure, depuis le départ de Gwenaëlle. Ainsi, t = 0 correspond au moment du départ de Gwenaëlle.
2. Soit g la fonction exprimant la distance parcourue par Gwenaëlle en fonction de t. Donner l'expression de cette fonction g.
3. Expliquer pourquoi la distance en kilomètre parcourue par Farid en fonction de t peut s'écrire 4 t+3. On appelle désormais cette fonction f.
4. On a tracé ci-dessous les représentations graphiques des fonctions f et g.
En justifiant, associer à chacune de ces courbes la fonction qui lui correspond.

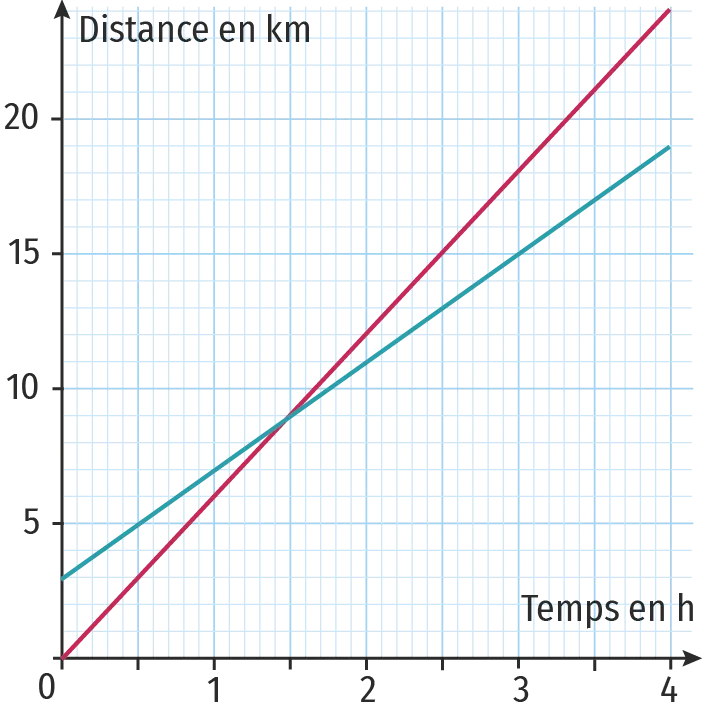
5. Déterminer le temps que mettra Gwenaëlle pour rattraper Farid :
a. par lecture graphique ;
b. en résolvant une équation.


5. Déterminer le temps que mettra Gwenaëlle pour rattraper Farid :
a. par lecture graphique ;
b. en résolvant une équation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26Chapitres et
Dans la figure suivante, les droites \text {(ED)} et \text {(AB)} sont parallèles. Le but de cet exercice est de déterminer les longueurs \text{ED} et \text{AC}.

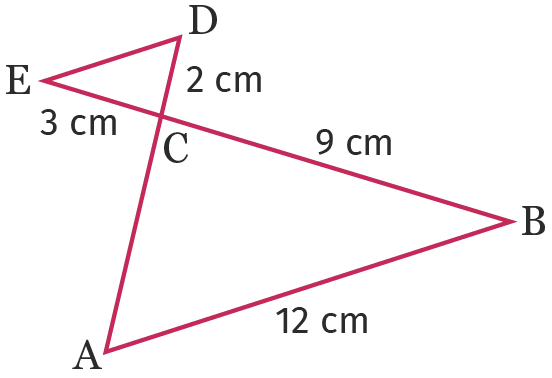 1. Reproduire la figure en vraie grandeur sur une feuille.
1. Reproduire la figure en vraie grandeur sur une feuille.
2. Tracer \mathrm{D}^{\prime} le symétrique de \text{D} par rapport à \text{C} et \mathrm{E}^{\prime} le symétrique de \text{E} par rapport à \text{C}.


3. Que peut-on dire des triangles \text{CED} et
\mathrm{CE}^{\prime} \mathrm{D}^{\prime} ? Justifier.
4. Démontrer que la droite \left(\mathrm{E}^{\prime} \mathrm{D}^{\prime}\right) est parallèle à (\mathrm{AB}).
4. Démontrer que la droite \left(\mathrm{E}^{\prime} \mathrm{D}^{\prime}\right) est parallèle à (\mathrm{AB}).
5. Déterminer les longueurs \mathrm{E}^{\prime} \mathrm{D}^{\prime} et \text{AC}.
6. En déduire la longueur \text{ED}.
6. En déduire la longueur \text{ED}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27Chapitres et
On considère l'expression littérale \mathrm{A}=\frac{9 n+9}{3}-\frac{8 n+12}{4} qui dépend d'un nombre~n.
1. Évaluer \text{A} lorsque n=1, n=-2 et n=\frac{5}{3}. Quelle conjecture peut-on faire ?
2. a. Montrer que l'on peut écrire
\mathrm{A}=\frac{4 \times(9 n+9)-3 \times(8 n+12)}{12}.
b. Développer puis simplifier au maximum cette expression. Retrouve-t-on le résultat conjecturé lors de la question 1 ?
1. Évaluer \text{A} lorsque n=1, n=-2 et n=\frac{5}{3}. Quelle conjecture peut-on faire ?
2. a. Montrer que l'on peut écrire
\mathrm{A}=\frac{4 \times(9 n+9)-3 \times(8 n+12)}{12}.
b. Développer puis simplifier au maximum cette expression. Retrouve-t-on le résultat conjecturé lors de la question 1 ?
3. a. Factoriser l'expression 9 n+9 par \text{3}.
b. En utilisant le résultat de la question précédente, simplifier \frac{9 n+9}{3}.
c. De la même manière, simplifier \frac{8 n+12}{4}.
d. Simplifier l'écriture de \text{A}. Retrouve-t-on le résultat conjecturé lors de la question 1 ?
b. En utilisant le résultat de la question précédente, simplifier \frac{9 n+9}{3}.
c. De la même manière, simplifier \frac{8 n+12}{4}.
d. Simplifier l'écriture de \text{A}. Retrouve-t-on le résultat conjecturé lors de la question 1 ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille