Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Exprimer un angle
❯
Mesure et unités
Un angle (noté \theta) s'exprime souvent en degrés (°) ou en radians (rad).
On utilise un rapporteur pour le mesurer.
Un angle (noté \theta) s'exprime souvent en degrés (°) ou en radians (rad).
On utilise un rapporteur pour le mesurer.

❯ Conversions d'unités
Un tour de cercle complet représente 360° ou 2 \pi \mathrm{rad}. On se sert de cette relation de proportionnalité pour convertir les mesures.
Exemple : L'angle mesuré ci-contre est de 35°.
Convertir cette mesure en radians : \theta(\mathrm{rad})=\dfrac{35 \times 2 \pi}{360}=0\text{,}61\, \mathrm{rad}
Un tour de cercle complet représente 360° ou 2 \pi \mathrm{rad}. On se sert de cette relation de proportionnalité pour convertir les mesures.
Exemple : L'angle mesuré ci-contre est de 35°.
Convertir cette mesure en radians : \theta(\mathrm{rad})=\dfrac{35 \times 2 \pi}{360}=0\text{,}61\, \mathrm{rad}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Longueur d'un arc de cercle
❯ Angle quelconque
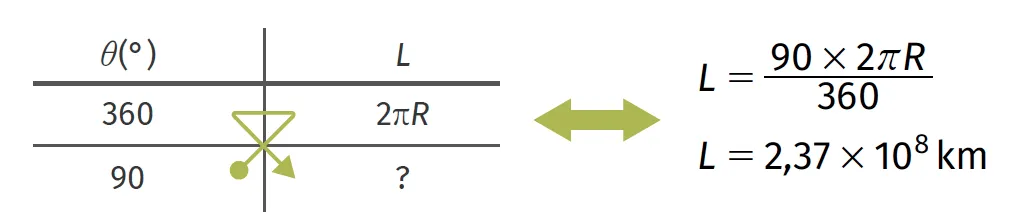
Le périmètre P du cercle mesure 2 \pi R et correspond à un angle \theta = 360°.
On se sert de la proportionnalité entre la longueur de l'arc et l'angle.
Exemple : Pour calculer la distance L parcourue par la Terre en 3 mois (¼ de tour de Soleil, donc un angle de 90°) : R=d_{\text {Terre-Soleil }}=150 \times 10^{6} km
Le périmètre P du cercle mesure 2 \pi R et correspond à un angle \theta = 360°.
On se sert de la proportionnalité entre la longueur de l'arc et l'angle.
Exemple : Pour calculer la distance L parcourue par la Terre en 3 mois (¼ de tour de Soleil, donc un angle de 90°) : R=d_{\text {Terre-Soleil }}=150 \times 10^{6} km

l = longueur du segment \text{[AB]}
L = longueur de l'arc
\theta = angle au centre délimitant l'arc \widehat{\mathrm{AB}}

❯ Si l'angle \theta est petit
L est alors très proche de l : on peut alors considérer que L = l.
Mesurer directement l à la règle par exemple.
L est alors très proche de l : on peut alors considérer que L = l.
Mesurer directement l à la règle par exemple.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C Relations de trigonométrie
❯ Définitions
\cos (\theta)=\dfrac{\operatorname{adj}}{\operatorname{hyp}}=\dfrac{\mathrm{AC}}{\mathrm{AB}}
\sin (\theta)=\dfrac{\text { opp }}{\text { hyp }}=\dfrac{\mathrm{BC}}{\mathrm{AB}}
\tan (\theta)=\dfrac{\sin (\theta)}{\cos (\theta)}=\dfrac{\mathrm{opp}}{\mathrm{adj}}=\dfrac{\mathrm{BC}}{\mathrm{AC}}
Faire l'unité d'angle sur la calculatrice.
\cos (\theta)=\dfrac{\operatorname{adj}}{\operatorname{hyp}}=\dfrac{\mathrm{AC}}{\mathrm{AB}}
\sin (\theta)=\dfrac{\text { opp }}{\text { hyp }}=\dfrac{\mathrm{BC}}{\mathrm{AB}}
\tan (\theta)=\dfrac{\sin (\theta)}{\cos (\theta)}=\dfrac{\mathrm{opp}}{\mathrm{adj}}=\dfrac{\mathrm{BC}}{\mathrm{AC}}
Faire l'unité d'angle sur la calculatrice.

❯ Calculer l'angle à partir de la valeur du cosinus, du sinus ou de la tangente
Utiliser les fonction arccos (aussi écrit cos-1), arcsin (sin-1) ou arctan (tan-1) de la calculatrice (en couleur au dessus des touches cos, sin ou tan.
Accessibles avec la touche
Accessibles avec la touche
SHIFT
ou 2nde
.
Ex : Si \text{BC} = 4 cm et \text{AB} = 6 cm
\sin (\theta)=\dfrac{\mathrm{BC}}{\mathrm{AB}}=\dfrac{4}{6}=0\text{,}67
\theta=\sin ^{-1}(0\text{,}67)=42^{\circ}=0\text{,}73 rad
\sin (\theta)=\dfrac{\mathrm{BC}}{\mathrm{AB}}=\dfrac{4}{6}=0\text{,}67
\theta=\sin ^{-1}(0\text{,}67)=42^{\circ}=0\text{,}73 rad
Fermer
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
