Fiche méthode 9
Outils mathématiques
La lecture graphique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Trouver les informations générales

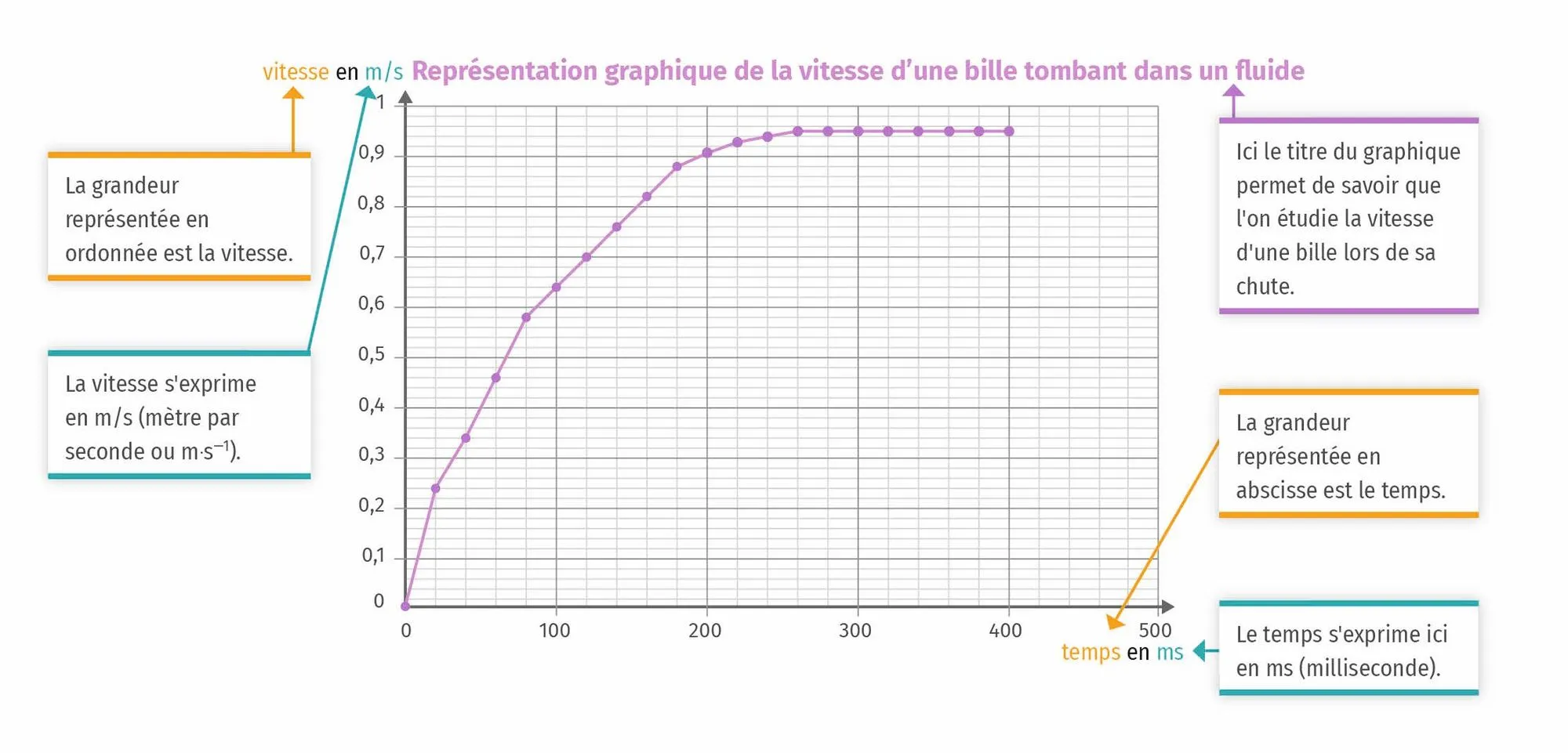
❯ Pour lire, analyser et exploiter un graphique, il faut toujours procéder par les mêmes étapes :
- identifier et comprendre le titre (de quoi parle ce graphique) ;
- relever la grandeur représentée par chacun des axes, l'axe vertical est l'axe des ordonnées et l'axe horizontal est l'axe des abscisses ;
- repérer les unités et les associer aux grandeurs concernées ;
- comprendre les échelles utilisées pour les deux axes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
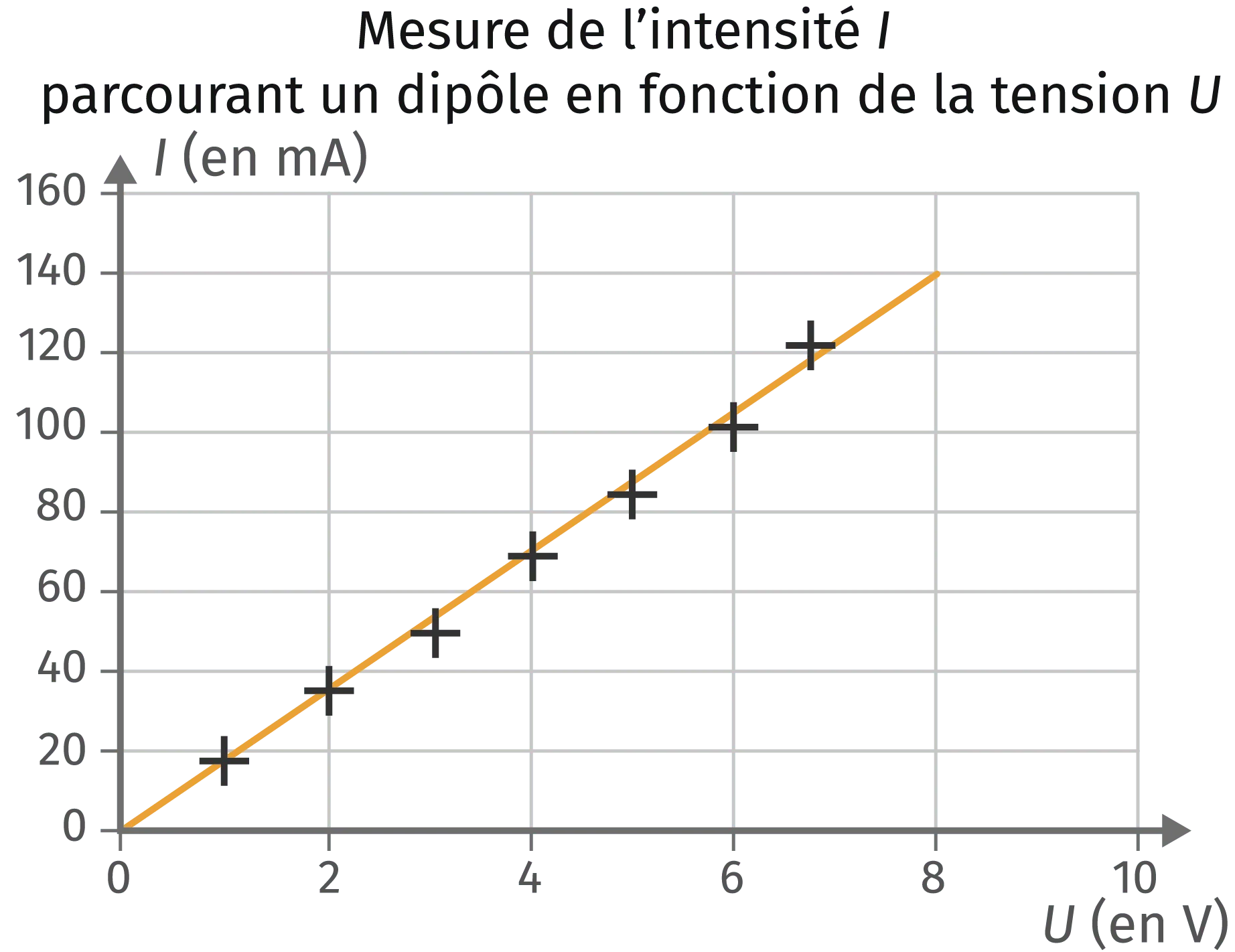
BIdentifier la linéarité et l'interpréter
- Reconnaître une situation de linéarité. Dans certaines situations, lorsque l'on représente dans un graphique une grandeur A en fonction d'une grandeur B, les points placés dessinent une droite qui passe par l'origine du repère. Même si les points ne sont pas parfaitement alignés, on dessine alors une droite moyenne qui passe le plus près de chaque point.
- Interpréter la linéarité. Tracer une droite moyenne signifie que le physicien interprète ses résultats comme témoignant de la proportionnalité entre les deux grandeurs.
- Proportionnalité et linéarité. La relation entre deux grandeurs proportionnelles peut être traduite mathématiquement par une égalité mathématique de la forme : B=\text{k} \cdot A.
- k est appelé coefficient de proportionnalité et correspond à la pente de la droite moyenne.
- Déterminer la valeur du coefficient de proportionnalité. Pour déterminer la valeur de la pente de la droite, il faut lire les coordonnées (a ; b) d'un point situé sur la droite moyenne. La valeur k de la pente de la droite est alors \mathrm{k}=\dfrac{b}{a} et son unité est l'unité de a divisée par celle de b.

Fermer
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
