Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Automatismes
Ch. 1
Statistiques à une variable
Ch. 2
Fluctuations d'une fréquence et probabilités
Ch. 3
Résolution d'un problème du premier degré
Ch. 4
Représentation et variations d'une fonction
Ch. 5
Fonctions affines, fonction carré
Ch. 6
Calculs commerciaux et financiers
Ch. 7
Géométrie
Fiches méthodes
Chapitre 2
L'essentiel
Fluctuations d'une fréquence et probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
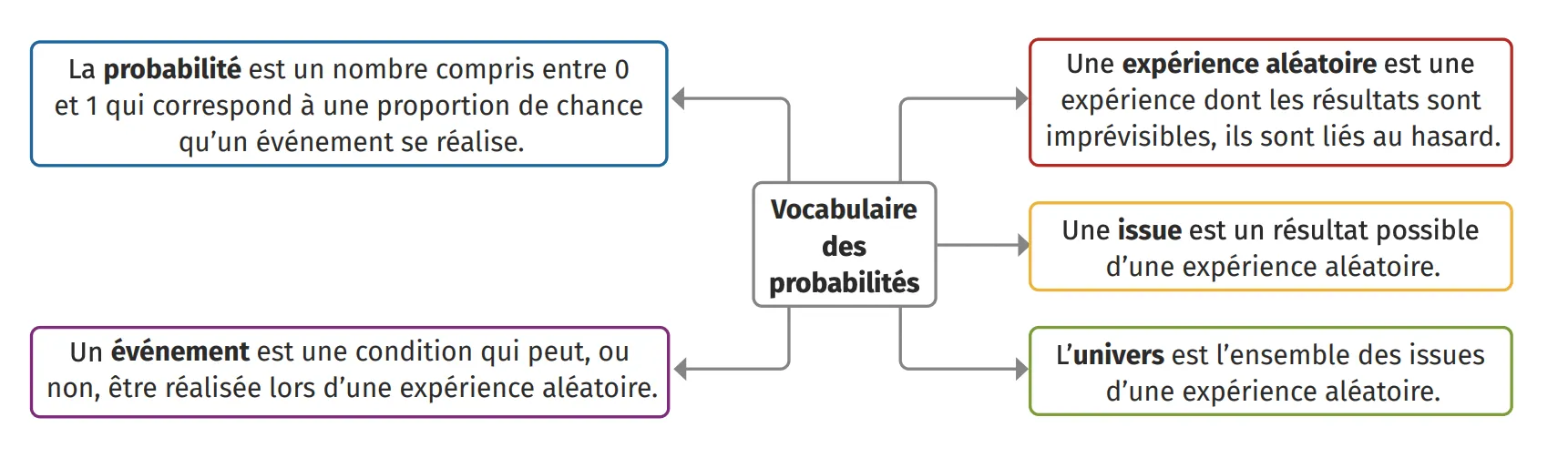
1Vocabulaire des probabilités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On considère l'expérience aléatoire qui consiste à lancer un dé à six faces. Cette expérience possède six issues qui sont : 1 ; 2 ; 3 ; 4 ; 5 et 6. On note l'univers {\Omega=\text{\{1 ; 2 ; 3 ; 4 ; 5 ; 6\}}.}
On note l'événement \mathrm{A} : « Obtenir un nombre pair » dont on peut calculer la probabilité : {p(\mathrm{~A})=\frac{3}{6}=0,5}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
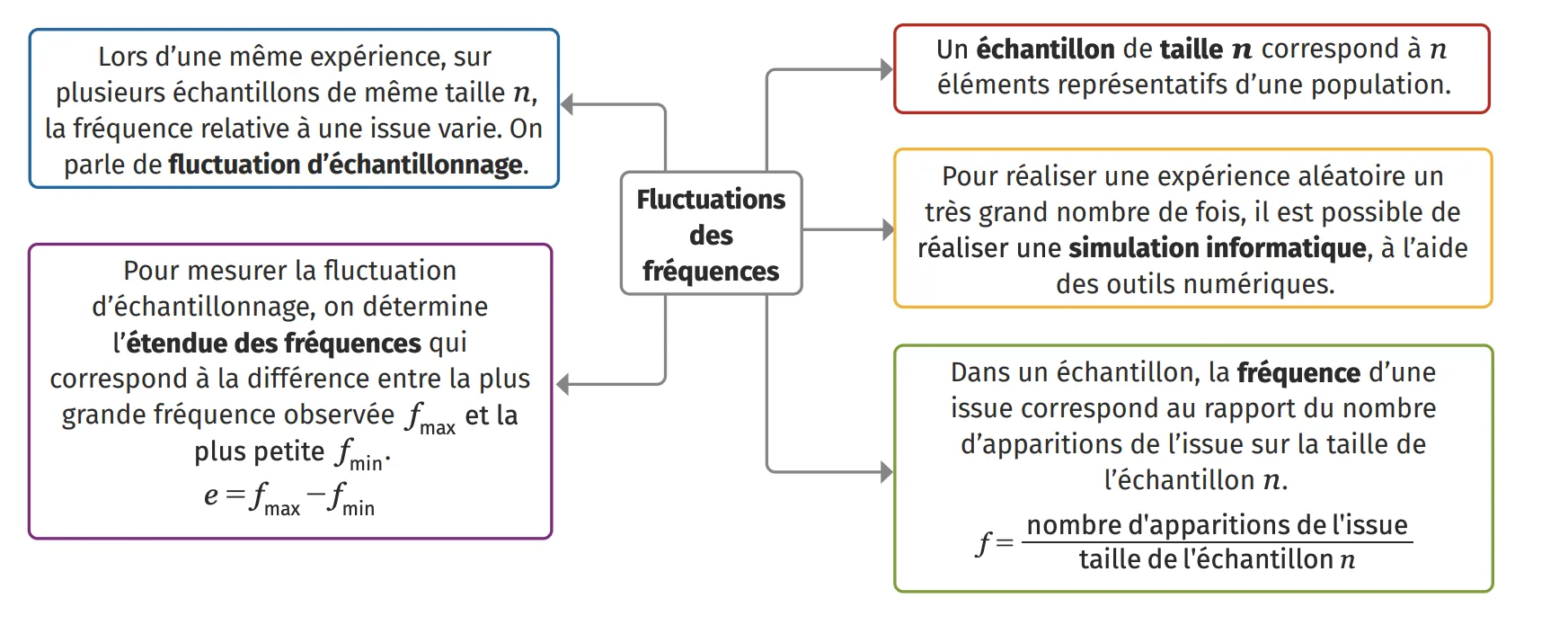
Fluctuations des fréquences
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On a réalisé la simulation informatique de
dix échantillons de taille n = 20, n = 100 et n = 1 000 lancers d'un dé à six faces, à l'aide du tableur. La fréquence de
sortie du 3 est représentée graphiquement ci-après.
- On observe que, pour des échantillons de même taille n, la fréquence de sortie du 3 varie : c'est ce que l'on appelle la fluctuation d'échantillonnage.
- On observe que plus la taille n de l'échantillon augmente, plus l'étendue des fréquences diminue, on dit que la fluctuation diminue.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Probabilité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définitions
- La probabilité d'un événement est une valeur théorique qui correspond au rapport du nombre de cas favorables à l'événement sur le nombre de cas possibles.
p=\frac{\text { nombre de cas favorables }}{\text { nombre de cas possibles }}
- Lorsqu'une expérience est réalisée un très grand nombre de fois n, la fréquence observée se stabilise vers une valeur proche de la probabilité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
On considère l'expérience aléatoire
qui consiste à lancer plusieurs fois
un dé à six faces et on représente
graphiquement la fréquence de sortie
du 6 ci-après.
On note \mathrm{A} l'événement « Obtenir le chiffre 6 ».
On note \mathrm{A} l'événement « Obtenir le chiffre 6 ».
- On observe que plus le nombre de lancers augmente, plus la fréquence de sortie du 6 se stabilise vers la valeur 0,17.
- On calcule la probabilité de l'événement \mathrm{A} : p(\mathrm{A})=\frac{1}{6} \approx 0,167
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Il est possible de représenter les différentes issues d'une expérience aléatoire sous la forme :
- d'un tableau à double entrée ;
- d'un arbre de dénombrement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice résolu
Lors d'une fête foraine, Théo participe à un jeu dans lequel il doit lancer une pièce de monnaie deux
fois successivement. Il remporte une peluche s'il obtient deux fois « face ».
1. Compléter le tableau à double entrée ci-après.
| 2e lancer | |||
|---|---|---|---|
| Pile | Face | ||
| 1er lancer | Pile | PP | PF |
| Face | FP | FF | |
2. Compléter l'arbre de dénombrement ci-après.
Le zoom est accessible dans la version Premium.
3. Indiquer les différentes issues possibles.
4. Calculer la probabilité que Théo gagne une peluche.
Les 4 issues possibles sont : PP ; PF ; FP ; FF.
4. Calculer la probabilité que Théo gagne une peluche.
La probabilité que Théo gagne une peluche correspond à la probabilité d'obtenir deux fois « face » lors de deux lancers
successifs d'une pièce de monnaie :
p(F F)=\frac{\text { nombre de cas favorables }}{\text { nombre de cas possibles }}=\frac{1}{4}=0,25.
p(F F)=\frac{\text { nombre de cas favorables }}{\text { nombre de cas possibles }}=\frac{1}{4}=0,25.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah