Sommaire
Mes pages
N° Page
ouverture
p. 1-13
Réviser avec Genially
Genially
/ 157
Page précédente
Chapitre 2

Exercices de consolidation

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Vocabulaire des probabilités

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

7

On lance un dé à dix faces non pipé et on relève la face du dessus.
Placeholder pour Illustration d'un dé à huit faces vert, avec les chiffres 0, 2, 3 et 8 visibles.Illustration d'un dé à huit faces vert, avec les chiffres 0, 2, 3 et 8 visibles.
1. Indiquer si cette expérience est une expérience aléatoire, en justifiant.
 2. Indiquer le nombre total d'issues de cette expérience.
 3. Indiquer les différentes issues de cette expérience.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

8

Pour chacune des expériences suivantes, indiquer s'il s'agit, ou non, d'une expérience aléatoire, en justifiant.
1. Lancer une pièce de monnaie équilibrée.
 2. Obtenir le baccalauréat.
 3. Tirer une boule indiscernable au toucher dans une urne opaque.
4. Répondre à un QCM d'anglais.
 5. Choisir le thème « paysages » ou « animaux » lors de l'achat d'un calendrier.
 6. Lancer un dé pipé à six faces.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Fluctuations des fréquences

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

9

On réalise plusieurs lancers de dés à six faces et on obtient les résultats ci-après.

Placeholder pour Illustration : douze dés noirs à points jaunes montrant tous les résultats possibles d'un lancer de dé.Illustration : douze dés noirs à points jaunes montrant tous les résultats possibles d'un lancer de dé.
1. Indiquer la taille de cet échantillon.
 2. Indiquer les différentes issues possibles de cette expérience aléatoire.
 3. Calculer la fréquence de sortie du 4 dans cet échantillon.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

10

Situation A : On a réalisé 5 échantillons de 50 lancers d'une pièce de monnaie en notant le nombre de « pile » obtenus dans le tableau suivant.
N° de l'échantillon 1 2 3 4 5
Nombre de « pile » obtenus 24 29 28 26 20
Situation B : En parallèle, on a réalisé la simulation informatique de 5 échantillons de 500 lancers d'une pièce de monnaie en notant les résultats dans le tableau suivant.
N° de l'échantillon 1 2 3 4 5
Nombre de « pile » obtenus 252 251 258 250 253
1. Pour chacune des situations, répondre aux questions suivantes.

a. Indiquer le nombre d'échantillons réalisés.
 b. Indiquer la taille n des échantillons.
c. Calculer la fréquence de « pile » obtenus pour chaque échantillon.
 d. Déterminer l'étendue des fréquences de « pile » obtenus.
2. Expliquer la différence d'étendue des fréquences de « pile » obtenus entre ces deux situations.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

11

On a réalisé une même expérience aléatoire en étudiant, d'une part, des échantillons de taille n=5 et, d'autre part, des échantillons de taille n=100 . On a résumé graphiquement les résultats de ces deux études ci-après.
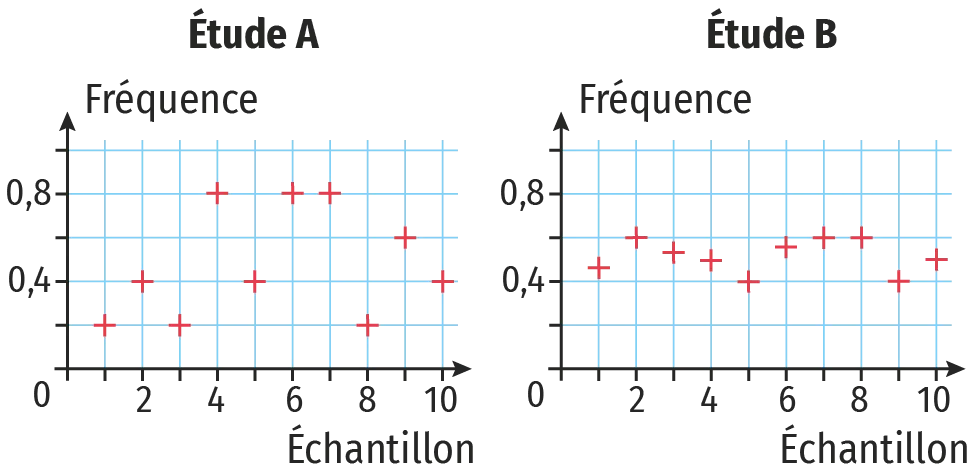
Placeholder pour Graphique: deux études (A et B) montrent la fréquence d'échantillons. Étude A : dispersion des données. Étude B : données plus groupées.Graphique: deux études (A et B) montrent la fréquence d'échantillons. Étude A : dispersion des données. Étude B : données plus groupées.

1. Indiquer le nombre d'échantillons réalisés lors de chaque étude.
 2. Déterminer l'étendue des fréquences pour chacune de ces deux études.
 3. En déduire laquelle de ces deux études correspond aux échantillons de taille n=100 , en justifiant.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

12
#Python

 On modélise une expérience aléatoire avec le programme en langage Python suivant. 
from random import *
a = randint(0,1)
print(a)

1. Exécuter ce programme dix fois et noter les résultats obtenus.
2. Indiquer les différentes issues possibles de cette expérience aléatoire.
 3. Calculer la fréquence de chacune des issues.
 4. Proposer une expérience aléatoire que pourrait modéliser ce programme.
 5. Modifier ce programme afin de pouvoir modéliser le lancer d'un dé à six faces.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Probabilités

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

13

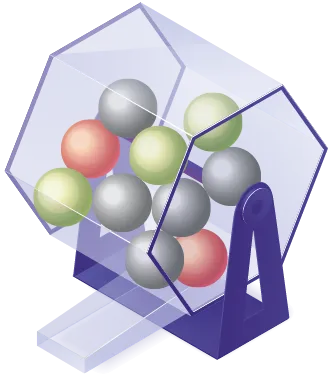
On tire une boule au hasard dans l'urne suivante.
1. Indiquer le nombre total de boules dans l'urne.
Placeholder pour Illustration : urne transparente contenant des boules de couleurs différentes pour un tirage au sort.Illustration : urne transparente contenant des boules de couleurs différentes pour un tirage au sort.
2. Calculer la probabilité de tirer : a. une boule rouge.
 b. une boule noire.
 c. une boule verte.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

14

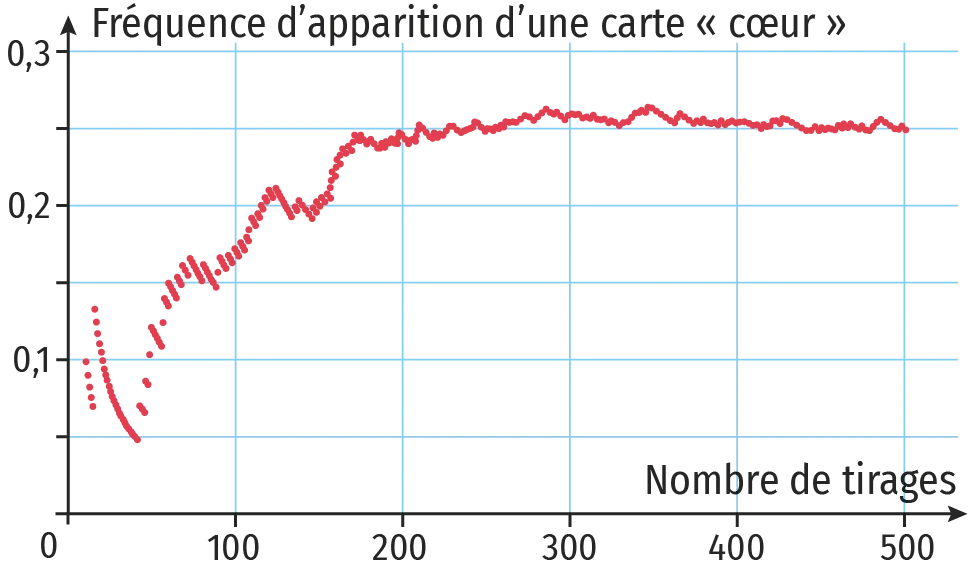
Placeholder pour Graphique montrant la fréquence d'apparition d'une carte cœur lors de tirages répétés.Graphique montrant la fréquence d'apparition d'une carte cœur lors de tirages répétés.
On a réalisé la simulation informatique de plusieurs tirages d'une carte, au hasard, dans un paquet de 32 cartes. On a représenté graphiquement la fréquence d'apparition d'une carte « cœur ».

1. Décrire comment évolue la fréquence d'apparition d'une carte « cœur » lorsque le nombre de tirages augmente.
 2. Déterminer la valeur vers laquelle semble se stabiliser cette fréquence.
3. Calculer la probabilité de tirer une carte « cœur » dans un paquet de 32 cartes.
 4. Comparer les valeurs obtenues aux questions 2. et 3. puis conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

15

« Dinogourou » est un jeu de société utilisant 30 cartes réparties comme indiqué dans le tableau ci-dessous.
Dinosaure Kangourou Total
Rouge 5 15 20
Bleu 5 5 10
Total 10 20 30
On tire une carte au hasard dans un paquet de cartes « Dinogourou ».

1. Calculer la probabilité de tirer une carte dinosaure.
 2. Calculer la probabilité de tirer une carte de couleur rouge.
 3. Calculer la probabilité de tirer un kangourou bleu.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

16

On lance une pièce de monnaie trois fois successivement et on note le résultat. On représente toutes les issues possibles par l'arbre ci-dessous.
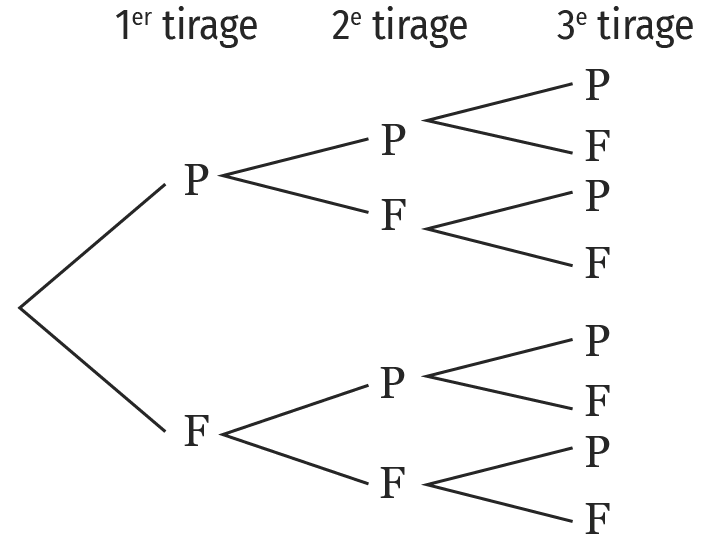
Placeholder pour Schéma en arbre de probabilités : trois tirages successifs avec succès (P) ou échec (F) à chaque étape.Schéma en arbre de probabilités : trois tirages successifs avec succès (P) ou échec (F) à chaque étape.
1. Indiquer le nombre total d'issues possibles.
 2. Indiquer le nombre d'issues où on a obtenu au moins deux fois « pile ».
 3. En déduire la probabilité de l'événement A : « Obtenir au moins deux fois “pile” ».
Page suivante

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille