Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 5
Entraînement 2
Limites de fonctions : définitions et premières propriétés
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37
Flash
À partir de la définition de \lim\limits_{\substack{ x \to +\infty }} f(x) = +\infty, donner une définition de \lim\limits_{\substack{ x \to +\infty }} f(x) = -\infty et de \lim\limits_{\substack{ x \to -\infty }} f(x) = +\infty
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Louis-Augustin Cauchy
(1789-1857) a donné au début de son Cours d'analyse (1821) la définition suivante de la notion de limite : « Si les valeurs successivement attribuées à une variable s'approchent indéfiniment d'une valeur fixe, de manière à finir par en différer aussi peu que l'on voudra, alors cette dernière est appelée la limite de toutes les autres. »
Il a fallu attendre Karl Weierstrass (1815-1897), considéré comme le père de l'analyse moderne, pour avoir donné, dans les années 1860, une définition purement logique de cette notion avec notamment l'utilisation de \delta et \epsilon.
Il a fallu attendre Karl Weierstrass (1815-1897), considéré comme le père de l'analyse moderne, pour avoir donné, dans les années 1860, une définition purement logique de cette notion avec notamment l'utilisation de \delta et \epsilon.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38
Flash
Soit f la fonction définie sur \R par f(x) = x^2 - 2x.
1. Existe-t-il une valeur m telle que, si x > m, alors f(x)>10^4 ?
2. Existe-t-il une valeur m telle que, si x > m, alors f(x)>10^{32} ?
3. Conjecturer la limite de f quand x tend vers +\infty.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39
Flash
Soit f la fonction définie sur \R par f(x)= \dfrac{1}{x^2 + 1} .
1. Existe-t-il une valeur m telle que, si x > m, alors 0 \lt f(x) \lt 10^{-4} ?
2. Existe-t-il une valeur m telle que, si x > m, alors 0 \lt f(x) \lt 10^{-32} ?
3. Conjecturer la limite de f quand x tend vers +\infty.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
[Communiquer.]
On donne ci-dessous la représentation graphique d'une fonction f définie sur \mathcal{D}_f.
Le zoom est accessible dans la version Premium.
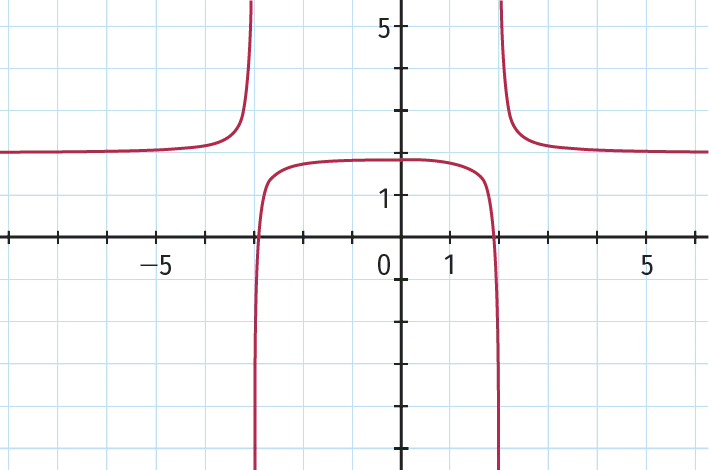
1. Déterminer graphiquement \mathcal{D}_f.
2. Conjecturer le tableau de variations de f sur \mathcal{D}_f ainsi que les limites éventuelles de f aux bornes de \mathcal{D}_f.
3. Déterminer une équation de chacune des éventuelles asymptotes.
2. Conjecturer le tableau de variations de f sur \mathcal{D}_f ainsi que les limites éventuelles de f aux bornes de \mathcal{D}_f.
3. Déterminer une équation de chacune des éventuelles asymptotes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
[Communiquer.]
On donne ci-dessous la représentation graphique d'une fonction f définie sur \R.
Le zoom est accessible dans la version Premium.
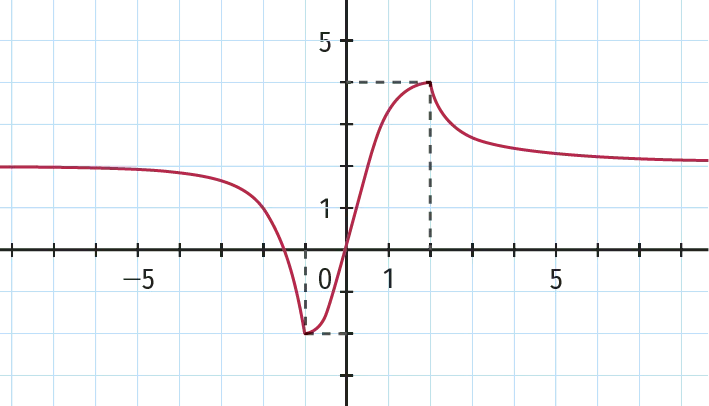
Conjecturer le tableau de variations de f sur \R, les limites éventuelles de f en -\infty et +\infty ainsi qu'une équation de chacune des éventuelles asymptotes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
[Représenter.]
Soit f une fonction définie et dérivable sur \R \setminus \{-1 ; 2\} dont on donne le tableau de variations ci-dessous.
Le zoom est accessible dans la version Premium.
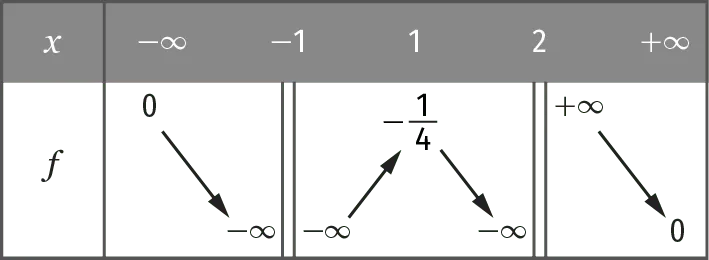
1. Déterminer les limites (ou limite à droite et à gauche) de f en -\infty, +\infty, -1 \;\text{et} \;2.
2. Donner une équation de chaque asymptote.
3. Tracer une représentation graphique possible de la fonction f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
[Représenter.]
Soit f une fonction définie et dérivable sur \R dont on donne le tableau de variations ci-dessous.
Le zoom est accessible dans la version Premium.
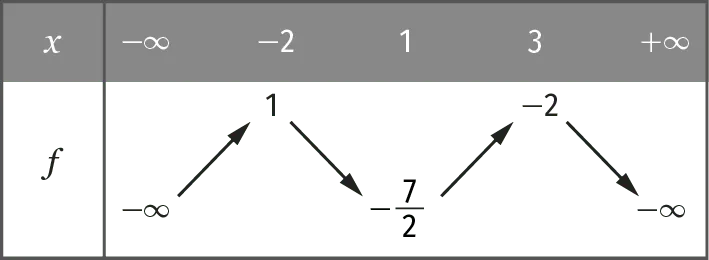
1. Déterminer les limites de f en -\infty et en +\infty, puis donner les équations des éventuelles asymptotes.
2. Tracer une représentation graphique possible de la fonction f .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
GeoGebra
[Représenter.]
Soit f la fonction définie sur \R \setminus \{2\} par f(x) = \dfrac{3x^3 - x + 1}{x^3 - 8}.
1. Représenter graphiquement cette fonction en utilisant GeoGebra ou la calculatrice.
1. Représenter graphiquement cette fonction en utilisant GeoGebra ou la calculatrice.
GeoGebra
2. Quelles limites peut-on conjecturer ?
3. Donner les équations des éventuelles asymptotes.
3. Donner les équations des éventuelles asymptotes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
GeoGebra
[Représenter.]
Soit f la fonction définie sur \R par f(x) = x (\sin(x) + 2).
1. Représenter graphiquement cette fonction en utilisant GeoGebra ou la calculatrice.
GeoGebra
2. La fonction f semble-t-elle avoir des limites en +\infty et -\infty ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
Démo
[Raisonner.]
On souhaite démontrer que la fonction f définie sur \R par f(x) = x^2 a pour limite +\infty en +\infty.
1. Déterminer une valeur m telle que, si x > m, alors f(x) > 10^4.
2. Soit A > 0. Démontrer qu'il existe une valeur m telle que, si x > m, alors f(x) > A.
3. Conclure.
2. Soit A > 0. Démontrer qu'il existe une valeur m telle que, si x > m, alors f(x) > A.
3. Conclure.
4. Généralisation : soit g la fonction définie sur \R par g(x) = x^n, où n est un entier naturel non nul.
a. En utilisant un raisonnement analogue que pour x^2, démontrer que g a pour limite +\infty lorsque x \rightarrow +\infty.
b. Selon la parité de n, exprimer g(-x) en fonction de g(x).
c. En déduire alors la limite de g en -\infty en fonction de la parité de n et en utilisant les limites en +\infty.
a. En utilisant un raisonnement analogue que pour x^2, démontrer que g a pour limite +\infty lorsque x \rightarrow +\infty.
b. Selon la parité de n, exprimer g(-x) en fonction de g(x).
c. En déduire alors la limite de g en -\infty en fonction de la parité de n et en utilisant les limites en +\infty.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
[Raisonner.]
Soit f la fonction définie sur \R par f(x) = 2x^2 - 3x.
1. Déterminer une valeur m telle que, si x > m, alors f(x) > 10^4.
2. Soit \text{A} > 0. Démontrer qu'il existe une valeur m telle que, si x > m, alors f(x) > \text{A}.
3. Conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
Démo
[Raisonnner.]
1. Soient f la fonction racine carrée et \text{A} un nombre réel positif.
a. Justifier que, si x > \text{A}^2, alors f(x) > \text{A}.
b. Que peut-on en conclure sur la limite de f en +\infty ?
2. Soit g la fonction définie, pour tout réel x strictement positif, par g(x) = \dfrac{1}{\sqrt{x}} .
a. Déterminer une valeur m telle que, si x > m, alors 0 \lt g(x) \lt 10^{-4}.
b. Soit \epsilon > 0. Démontrer qu'il existe une valeur m telle que, si x > m, alors 0 < g(x) < \epsilon.
c. Conclure.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah