Chapitre 1
Entrainement 1
Généralités
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40
[Calculer.]
Pour chacune des suites suivantes, calculer u_0 , u_1 , u_2 ,
u_3 , u_4 et u_{10} lorsque c'est possible.
1. u_{n}=\sqrt{n-1}+2 n
2. u_{n}=\dfrac{5 n-3}{2 n-2}
2. u_{n}=\dfrac{5 n-3}{2 n-2}
3. u_{n}=\cos \left(n \dfrac{\pi}{2}\right)
4. u_{n}=\left(\dfrac{1}{2}\right)^{n}
4. u_{n}=\left(\dfrac{1}{2}\right)^{n}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41
Tableur
[Calculer.]
On souhaite calculer les termes d'une suite à l'aide d'un tableur.

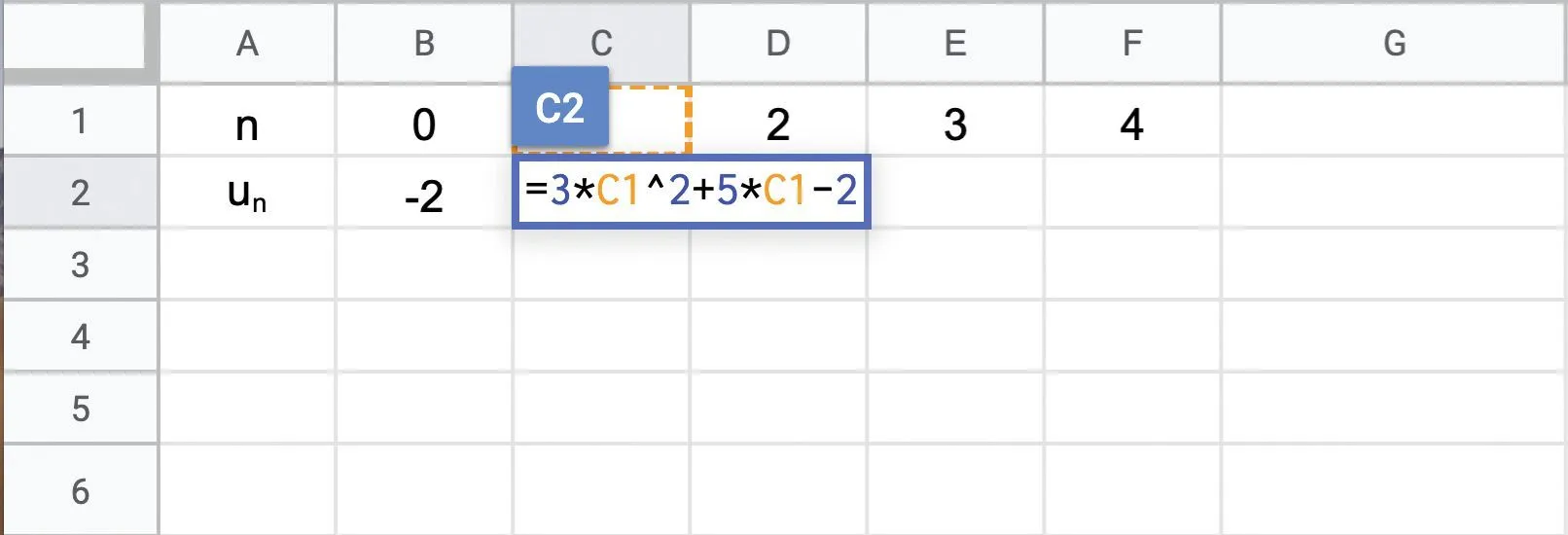
2. Exprimer le terme général u_n en fonction de n en utilisant la formule donnée par le tableur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42
Algo
[Calculer.]
On considère l'algorithme suivant :
\boxed{
\begin{array} { l } { \text {Pour i allant de } 1 \text{ à } 10 :} \\
\quad \text {U } \leftarrow 2\text{i} -1\\
\text {Fin Pour}
\end{array}
}
1. Quelle sera la dernière valeur calculée par cet algorithme ?
2. On appelle (u_n) la suite associée aux valeurs calculées par l'algorithme.
Donner l'expression du terme général de cette suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43
[Calculer.] Pour chacune des suites suivantes définies sur \N, exprimer u_{n-1} et u_{n+1} en fonction de n : 1. u_{n}=6 n+8
2. u_{n}=n^{2}-2 n+8
3. u_{n}=\dfrac{n(n+1)}{n+2}
4. u_{n}=5^{n}
5. u_{n}=\dfrac{3^{n+1}}{2^{n}}
6. u_{n}=\dfrac{9 n-5}{4 n+6}
7. u_{n}=\left(\dfrac{n^{2}}{n+1}\right)^{n+1}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44
[Calculer.] Pour chacune des suites définies pour tout entier naturel n , calculer les trois termes suivant le premier. 1. \left\{\begin{array}{l}{u_{0}=2} \\ {u_{n+1}=3 u_{n}-4 n}\end{array}\right.
2. \left\{\begin{array}{l}{u_{0}=0} \\ {u_{n+1}=u_{n}^{2}+\dfrac{1}{2 n+1}}\end{array}\right.
3. \left\{\begin{array}{l}{u_{0}=3} \\ {u_{n}=5 u_{n-1}-2}\end{array}\right.
4. \left\{\begin{array}{l}{u_{0}=1} \\ {u_{1}=2} \\ {u_{n+2}=2 u_{n+1}+u_{n}}\end{array}\right.
5. \left\{\begin{array}{l}{u_{0}=1} \\ {u_{1}=2} \\ {u_{n+2}=u_{n+1}+n}\end{array}\right.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
[Calculer.]
Utiliser la calculatrice afin de faire afficher de la quatrième à la dixième valeur des deux suites suivantes définies sur \N.
1. \left\{\begin{array}{l}{u_{0}=2} \\ {u_{n+1}=n u_{n}+5}\end{array}\right.
2. \left\{\begin{array}{l}{u_{0}=-1} \\ {u_{n+1}=u_{n}^{2}-(n+2)}\end{array}\right.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
Tableur
[Modéliser.]
On souhaite calculer les termes d'une suite à l'aide d'un tableur.
Pour chacune des feuilles de calcul, écrire la relation donnant u_{n+1} en fonction de u_n .
1.

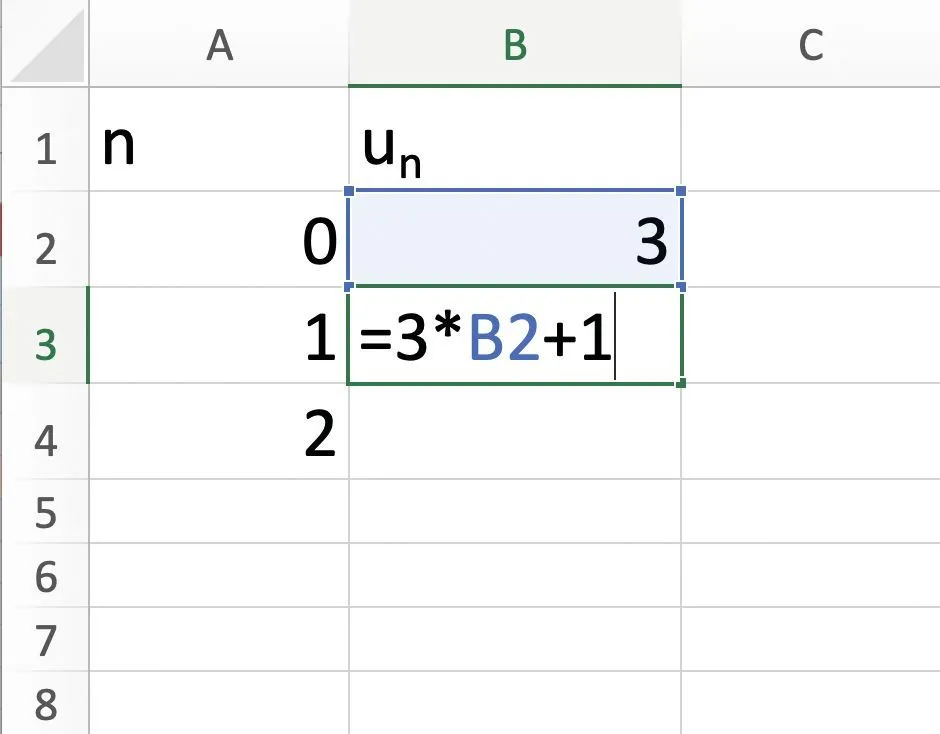


2.

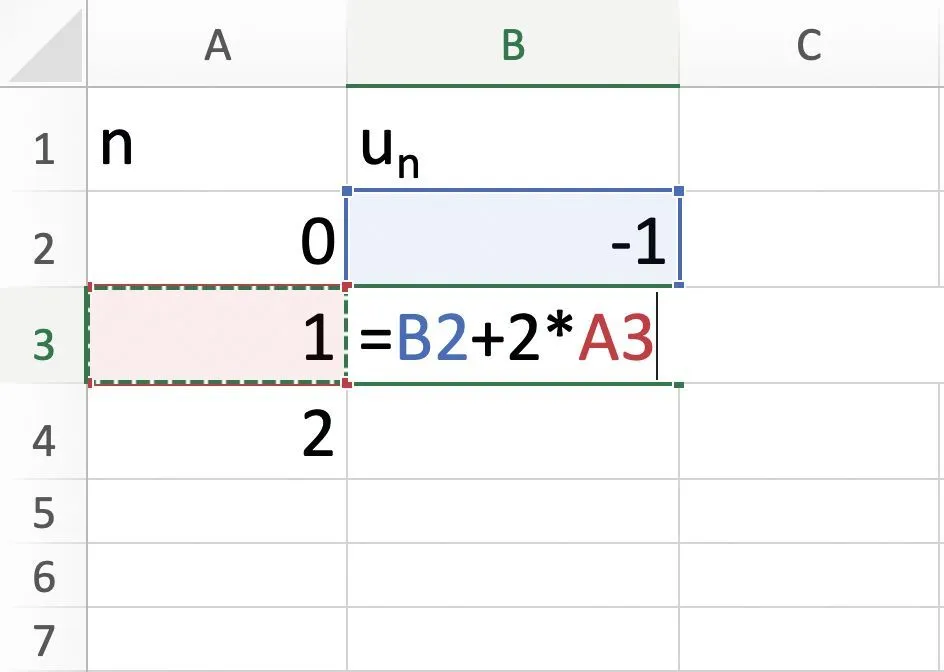


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
Algo
[Calculer.]
On considère l'algorithme ci-dessous définissant une suite \left(u_n\right)\::
\boxed{
\begin{array} { l } { \text {U} \leftarrow 1 } \\
\text {Pour i allant de } 1 \text{ à } 10 : \\
\quad \text {U} \leftarrow \dfrac{\text {U}-1}{\text {U}-2}\\
\text {Fin Pour}
\end{array}
}
1. Que calcule cet algorithme ?
2. Écrire une relation entre u_{n+1} et u_n.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
[Calculer.] Pour chacune des suites suivantes, définies sur \N, exprimer u_n en fonction de u_{n-1} pour tout entier n \geqslant 1 puis u_{n+2} en fonction de u_{n+1} pour tout entier n.
En déduire une expression de u_{n+2} en fonction de u_n et de l'entier n . 1. \left\{\begin{array}{l}{u_{0}=3} \\ {u_{n+1}=5 u_{n}-3}\end{array}\right.
2. \left\{\begin{array}{l}{u_{0}=1} \\ {u_{n+1}=4 u_{n}-(n-3)}\end{array}\right.
3. \left\{\begin{array}{l}{u_{0}=-1} \\ {u_{n+1}=(n+1) u_{n}+2}\end{array}\right.
4. \left\{\begin{array}{l}{u_{0}=-1} \\ {u_{n+1}=\dfrac{u_{n}^{2}}{2 n+3}}\end{array}\right.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
[Calculer.] Dans chaque cas, déterminer le sens de variation de la suite (u_n) définie par : 1. u_{n}=\dfrac{n+1}{n+2} pour tout n\geqslant 0
2. u_{n}=\dfrac{3^{n}}{n} pour tout n\geqslant 1
3. u_{n}=n^{2}-3 n+12 pour tout n\geqslant 0
4. u_{n}=\dfrac{1}{n}-\dfrac{1}{n+1} pour tout n\geqslant 1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
[Représenter.] Dans un repère orthonormé, on a représenté la fonction f définie sur \R par f(x) = 0{,}5x + 3 et la droite d'équation y = x .
On définit la suite (u_n) par \left\{\begin{array}{l}{u_{0}=1} \\ {u_{n+1}=f\left(u_{n}\right)}\end{array}\right.

1. Reproduire la figure et représenter les cinq premiers termes de la suite sur l'axe des abscisses.
2. Conjecturer le sens de variation de la suite \left(u_n\right).
3. Conjecturer la limite de la suite.
2. Conjecturer le sens de variation de la suite \left(u_n\right).
3. Conjecturer la limite de la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
[Représenter.]
Dans un repère orthonormé, on a représenté la fonction f définie sur \left] -2\, ;\, +\infty \right[ par f(x)=\dfrac{6}{x+2}-1 et la droite d'équation y = x .
On définit la suite (u_n) par \left\{\begin{array}{l}{u_{0}=5} \\ {u_{n+1}=f\left(u_{n}\right)}\end{array}\right.

1. Reproduire et représenter les cinq premiers termes de la suite sur l'axe des abscisses.
2. Émettre une conjecture sur le sens de variation de la suite, puis sur sa limite.
2. Émettre une conjecture sur le sens de variation de la suite, puis sur sa limite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
[Chercher.]
La suite (u_n) est définie par u_{n}=\dfrac{3 n-2}{n+1} pour tout entier naturel n .
1. Représenter graphiquement cette suite sur la calculatrice ou un logiciel. Conjecturer son sens de variation et sa limite.
2. Prouver la conjecture sur le sens de variation de la suite.
3. Montrer que pour tout n \geqslant 0 , -2 \leqslant u_{n} \leqslant 3.
4. Déterminer, par un calcul, l'entier n_0 à partir duquel on a u_n \geqslant 2{,}8 pour tout n\geqslant n_0 .
3. Montrer que pour tout n \geqslant 0 , -2 \leqslant u_{n} \leqslant 3.
4. Déterminer, par un calcul, l'entier n_0 à partir duquel on a u_n \geqslant 2{,}8 pour tout n\geqslant n_0 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
[Calculer.] Soit (u_n) la suite définie pour tout entier naturel n par u_{n}=5+\dfrac{3}{2 n+1}.
1. Calculer les cinq premiers termes de la suite (u_n).
2. Déterminer le sens de variation de (u_n).
3. Déterminer par le calcul le plus petit entier n_0 tel que \left|u_{n_0}-5\right| \leqslant 0{,}001.
4. Conjecturer la limite de la suite.
5. Question facultative :
a. Écrire un algorithme permettant de trouver le rang n_0 à partir duquel \left|u_{n_{0}}-5\right| \leqslant \varepsilon pour \varepsilon donné par l'utilisateur.
2. Déterminer le sens de variation de (u_n).
3. Déterminer par le calcul le plus petit entier n_0 tel que \left|u_{n_0}-5\right| \leqslant 0{,}001.
4. Conjecturer la limite de la suite.
5. Question facultative :
a. Écrire un algorithme permettant de trouver le rang n_0 à partir duquel \left|u_{n_{0}}-5\right| \leqslant \varepsilon pour \varepsilon donné par l'utilisateur.
b. Programmer l'algorithme et le tester pour \varepsilon = 0{,}001, \varepsilon=10^{-5} puis \varepsilon = 10^{-6}.
Fermer
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
