Enseignement scientifique Terminale
Mes Pages
Thème 1 : Science, climat et société
Introduction
Ch. 1
L'atmosphère terrestre et la vie
Ch. 2
La complexité du système climatique
Ch. 3
Le climat du futur
Ch. 4
Énergie, développement et futur climatique
Objectif Bac : Thème 1
Thème 2 : Le futur des énergies
Introduction
Ch. 5
Deux siècles d’énergie électrique
Ch. 6
Les atouts de l’électricité
Ch. 7
Optimisation du transport de l’électricité
Ch. 8
Choix énergétiques et impacts
Objectif Bac : Thème 2
Thème 3 : Une histoire du vivant
Introduction
Ch. 9
La biodiversité et son évolution
Ch. 10
L’évolution, une grille de lecture du monde
Ch. 11
L’évolution humaine
Ch. 12
Les modèles démographiques
Ch. 13
De l’informatique à l’intelligence artificielle
Objectif Bac : Thème 3
Livret maths
Fiches méthode
Annexes
Chapitre 12
Exercices
Le repaire des initiés
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14Exercice autocorrigé
Malthus et la croissance francilienne
✔ Utiliser le taux de variation pour prédire l'effectif d'une population
Pour un taux d'accroissement t, la population suit une suite géométrique de raison q = 1 + t.
.
En 2014, le taux de natalité francilien est de 1,52 %, alors que le taux de mortalité est de 0,6 %. L'Île-de-France compte 12 027 565 habitants au 1er janvier 2014 (données Insee).
En 2014, le taux de natalité francilien est de 1,52 %, alors que le taux de mortalité est de 0,6 %. L'Île-de-France compte 12 027 565 habitants au 1er janvier 2014 (données Insee).
Formule
Pour un taux d'accroissement t, la population suit une suite géométrique de raison q = 1 + t.
1. Calculer le taux d'accroissement de la population
selon Malthus.
2. Écrire le terme général de la suite u donnant la population francilienne au bout de n années, en prenant l'année 2014 pour le rang 0 selon ce modèle de croissance exponentielle.
3. Estimer alors la population francilienne en 2016.
4. Comparer cette estimation avec le nombre donné par l'Insee : 12 117 131 habitants.
2. Écrire le terme général de la suite u donnant la population francilienne au bout de n années, en prenant l'année 2014 pour le rang 0 selon ce modèle de croissance exponentielle.
3. Estimer alors la population francilienne en 2016.
4. Comparer cette estimation avec le nombre donné par l'Insee : 12 117 131 habitants.
Doc.
Avenue des Champs-Élysées, Paris.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15
Doublement de la population
✔ Calculer le temps de doublement d'une population sous l'hypothèse de croissance exponentielle
.
1. Calculer la population en 2014 (on pourra considérer une suite géométrique à préciser).
2. En considérant que ce taux d'accroissement reste inchangé, à l'aide de la calculatrice, déterminer à partir de quelle année la population aura doublé par rapport à celle de 2014.
3. En observant le graphique, on constate que la croissance est quasi linéaire. Déterminer alors une autre estimation de l'année à partir de laquelle la population aura doublé selon ce modèle linéaire.
.
1. Calculer la population en 2014 (on pourra considérer une suite géométrique à préciser).
2. En considérant que ce taux d'accroissement reste inchangé, à l'aide de la calculatrice, déterminer à partir de quelle année la population aura doublé par rapport à celle de 2014.
3. En observant le graphique, on constate que la croissance est quasi linéaire. Déterminer alors une autre estimation de l'année à partir de laquelle la population aura doublé selon ce modèle linéaire.
Doc. 1
Libreville, Gabon.
Doc. 2
Prévision de la population du Gabon.La population du Gabon est estimée à 1 995 659 habitants en 2018. On estime que le taux d'accroissement de 2,154 % est stable depuis 2014. Ces données sont représentées dans le graphique suivant :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16
Croissance bactériennète
✔ Interpréter des graphiques traduisant l'évolution d'une population
Les bactéries possèdent une forte vitesse de croissance, environ une génération toutes les vingt minutes dans des conditions favorables. Pour cette raison, on peut facilement les utiliser en laboratoire afin d'étudier les phénomènes d'évolution de populations dans différentes situations. Ci-dessous est tracée la courbe d'évolution d'une population de bactéries dans une boîte de Petri (milieu fermé, donc ressources limitées).
1. Identifier le type de croissance de la population bactérienne dans la phase 2.
2. Quelle différence existe-t-il du point de vue des ressources entre un milieu fermé et un milieu ouvert ? Expliquer alors l'allure de la courbe dans les phases 3 et 4 du doc. 2.
3. La courbe obtenue correspond-elle au modèle de Verhulst ou au modèle de Malthus ?
4. On place cette fois une colonie de bactéries identique dans un milieu ouvert. Tracer l'allure de la courbe de la population en vous inspirant de celle donnée en énoncé.
2. Quelle différence existe-t-il du point de vue des ressources entre un milieu fermé et un milieu ouvert ? Expliquer alors l'allure de la courbe dans les phases 3 et 4 du doc. 2.
3. La courbe obtenue correspond-elle au modèle de Verhulst ou au modèle de Malthus ?
4. On place cette fois une colonie de bactéries identique dans un milieu ouvert. Tracer l'allure de la courbe de la population en vous inspirant de celle donnée en énoncé.
Cliquez pour accéder à une zone de dessin
Doc. 1
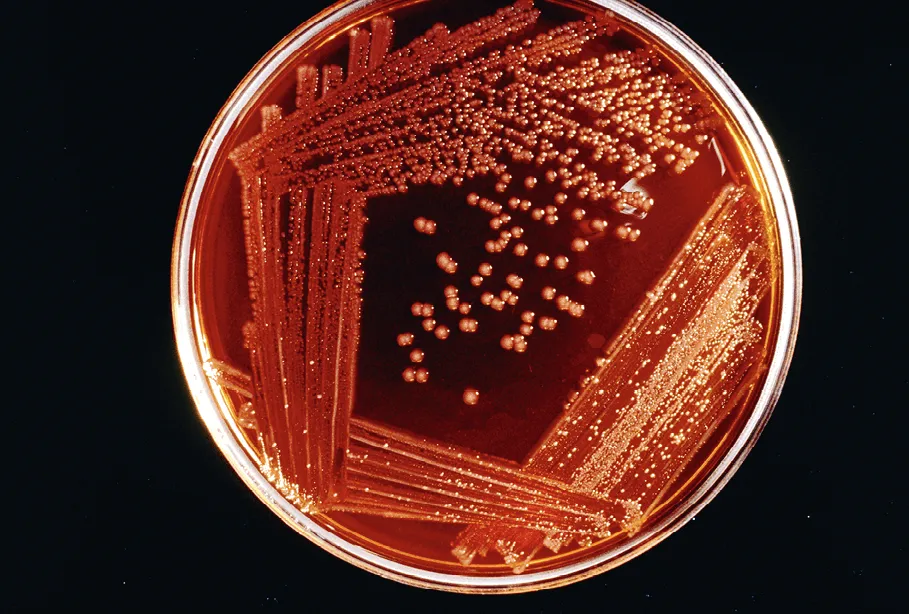
Colonies de bactéries dans une boîte de Petri.
Doc. 2
Évolution d'une population bactérienne dont les phases sont indiquées en orange.Les bactéries possèdent une forte vitesse de croissance, environ une génération toutes les vingt minutes dans des conditions favorables. Pour cette raison, on peut facilement les utiliser en laboratoire afin d'étudier les phénomènes d'évolution de populations dans différentes situations. Ci-dessous est tracée la courbe d'évolution d'une population de bactéries dans une boîte de Petri (milieu fermé, donc ressources limitées).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
Nourrir la planète
✔ Proposer un modèle de croissance de ressources alimentaires
et le comparer à une croissance exponentielle
La population mondiale en 2019 était estimée à 7713468000 habitants. Le taux de croissance prévu pour cette année est d'environ 1,08 %, soit une multiplication de la population d'un facteur 1,010 8.
1. Déterminer le type d'évolution de la production mondiale de blé. Déterminer alors l'équation u(n) de la production de blé, n représentant l'année.
2. En supposant que la production suive la même tendance, estimer la production mondiale de blé en 2100.
3. On suppose que la population mondiale suit une croissance qui respecte le modèle de Malthus : une croissance exponentielle. Calculer alors la population mondiale en 2100 selon ce modèle.
4. Comparer alors la production mondiale de blé en 2100 à l'estimation de la population mondiale selon Malthus (on pourra faire un rapport entre la population et la production en 2017, puis en 2100). Les prévisions malthusiennes sont-elles compatibles avec l'évolution des ressources ?
2. En supposant que la production suive la même tendance, estimer la production mondiale de blé en 2100.
3. On suppose que la population mondiale suit une croissance qui respecte le modèle de Malthus : une croissance exponentielle. Calculer alors la population mondiale en 2100 selon ce modèle.
4. Comparer alors la production mondiale de blé en 2100 à l'estimation de la population mondiale selon Malthus (on pourra faire un rapport entre la population et la production en 2017, puis en 2100). Les prévisions malthusiennes sont-elles compatibles avec l'évolution des ressources ?
Doc. 1
Production de blé.
Doc. 2
Population mondiale et croissance.La population mondiale en 2019 était estimée à 7713468000 habitants. Le taux de croissance prévu pour cette année est d'environ 1,08 %, soit une multiplication de la population d'un facteur 1,010 8.
Supplément numérique
Découvrir le film : .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CUne croissance linéaire
✔ Exprimer u(n) en fonction de u(0) et n pour une suite arithmétique
.
.
Le nombre d'habitants de la population des Hauts-de-France a augmenté d'environ 9 420 par an de 1990 à 1999. En 1990, il était de 5 770 671 habitants.
1. Déterminer la raison de la suite arithmétique u décrivant l'évolution de la population, dont le premier terme u(0) est la population en 1990.
2. Écrire alors le terme général de cette suite u.
3. En 2008, sa population était de 5 931 091. Calculer l'estimation en 2008 et la comparer avec la vraie valeur.
1. Déterminer la raison de la suite arithmétique u décrivant l'évolution de la population, dont le premier terme u(0) est la population en 1990.
2. Écrire alors le terme général de cette suite u.
3. En 2008, sa population était de 5 931 091. Calculer l'estimation en 2008 et la comparer avec la vraie valeur.
Doc.
Place du Général-de-Gaulle, Lille.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
DModèle de Malthus et réalite
✔ Comparer les valeurs fournies par un modèle à des données réelles afin de tester sa validité
.
.
La population allemande était estimée à 83019213 habitants en 2019. Son taux de natalité en 2013 était de 8,5 ‰, pour un taux de mortalité de 11,1 ‰. Le taux de croissance annuel était de 0,30 % en 2013
(Source : Eurostat).
1. En supposant que les taux de mortalité et de croissance restent constants, calculer le taux d'accroissement de la population selon Malthus.
2. Pour un taux d'accroissement t, l'effectif de la population suit une loi géométrique de raison q = 1 + t. Calculer cette raison et donner l'évolution attendue de cette population.
3. Le solde migratoire (différence entre le nombre de personnes entrant dans le pays et personnes sortant du pays) peut expliquer la différence entre le taux calculé et le taux observé. Déterminer si l'Allemagne a accueilli ou perdu de la population en fonction des phénomènes migratoires.
4. Calculer l'effectif théorique de la population en conservant le taux d'accroissement de 2013. Le comparer aux projections des démographes de 79 098 669 habitants en 2100.
1. En supposant que les taux de mortalité et de croissance restent constants, calculer le taux d'accroissement de la population selon Malthus.
2. Pour un taux d'accroissement t, l'effectif de la population suit une loi géométrique de raison q = 1 + t. Calculer cette raison et donner l'évolution attendue de cette population.
3. Le solde migratoire (différence entre le nombre de personnes entrant dans le pays et personnes sortant du pays) peut expliquer la différence entre le taux calculé et le taux observé. Déterminer si l'Allemagne a accueilli ou perdu de la population en fonction des phénomènes migratoires.
4. Calculer l'effectif théorique de la population en conservant le taux d'accroissement de 2013. Le comparer aux projections des démographes de 79 098 669 habitants en 2100.
Doc.
Porte de Brandebourg, Berlin.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
