Mathématiques Terminale Spécialité
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 1
TP INFO 1
Les mystérieux donateurs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
n personnes décident de jouer à un jeu. Chacun devra offrir un cadeau à une personne du groupe sélectionnée au hasard. Pour cela, on souhaite mettre en place un programme qui génère aléatoirement une permutation de l'ensemble des entiers naturels de 1 à n. Les participants sont numérotés de 1 à n.
Si le j-ième nombre de la permutation vaut i, alors la personne j devra faire un cadeau à la personne i.
Questions préliminaires :
1. Rappeler la définition d'une permutation d'un ensemble à n éléments.
2. Combien de permutations existe‑t‑il dans cette situation ?
Questions préliminaires :
1. Rappeler la définition d'une permutation d'un ensemble à n éléments.
2. Combien de permutations existe‑t‑il dans cette situation ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Pour un entier naturel \boldsymbol{n} non nul fixé, générer aléatoirement une permutation de l'ensemble des entiers naturels de 1 à \boldsymbol{n} en utilisant une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Python
On souhaite compléter le programme ci‑dessous. La fonction choice du module random permet de choisir uniformément au hasard un élément de la liste placée en argument.
from random import*
def permutation_alea(n) :
liste = list(range(... , ...))
resultat = []
for i in range(n) :
choix = choice(liste)
resultat ...
...
return resultat
1.
Compléter la ligne 4 afin de générer les entiers de 1 à n.
2. Compléter les lignes 8 et 9 pour ajouter l'élément choisi au résultat et le retirer des choix possibles.
3. Est‑on certain d'avoir généré une permutation de l'ensemble des entiers naturels de 1 à n avec ce programme ? Justifier.
2. Compléter les lignes 8 et 9 pour ajouter l'élément choisi au résultat et le retirer des choix possibles.
3. Est‑on certain d'avoir généré une permutation de l'ensemble des entiers naturels de 1 à n avec ce programme ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
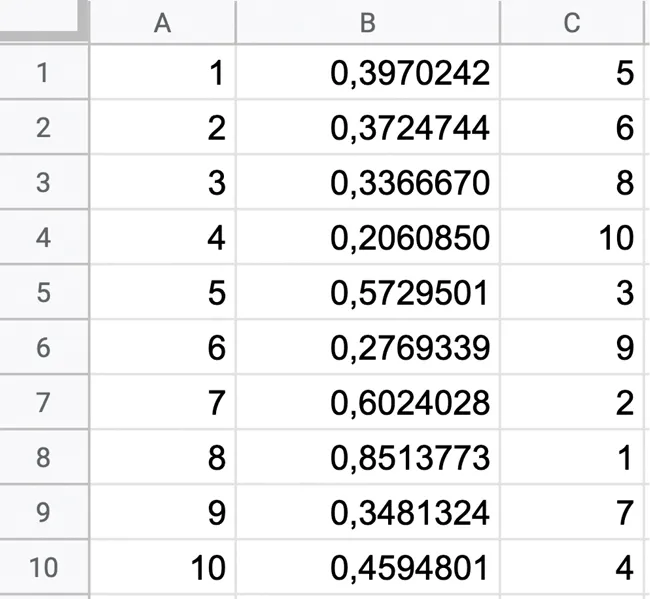
On prendra ici le cas n = 10.
1.
Dans la colonne A d'une feuille de calcul, inscrire les nombres entiers de 1 à 10.
2.
a.
Que permet de faire la formule \text{=ALEA()} ?
b.
Dans la cellule B1, entrer la formule \boldsymbol{\text{=ALEA()}} puis l'étirer vers le bas.
3.
Dans la colonne C, à l'aide de la formule RANG du tableur, classer les résultats de la colonne B de la plus grande valeur à la plus petite. On attribue ainsi à la plus grande valeur le nombre 1 et le nombre 10 à la plus petite.
On obtient un résultat semblable à celui ci‑dessous.
4.
Où la permutation générée se situe-t-elle ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ces méthodes ont un inconvénient : il se peut que les permutations aient un « point fixe », c'est-à-dire, dans notre cas, qu'un participant s'offre un cadeau à lui‑même.
Proposer une amélioration des méthodes décrites ci-dessus pour éviter ce désagrément.
Proposer une amélioration des méthodes décrites ci-dessus pour éviter ce désagrément.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
