Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 1
TP INFO 2
Le triangle de Pascal
10 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Le triangle de Pascal est une présentation des nombres de combinaisons de k éléments parmi n sous la forme d'un triangle : pour deux entiers naturels i et j avec i \geqslant j \geqslant 0, le nombre de la (i + 1)-ième ligne et de la (j + 1)-ième colonne vaut \left(\begin{array}{l}i\\j\end{array}\right).
Ce triangle peut être construit de proche en proche grâce à la relation de Pascal : un coefficient dans ce tableau est égal à la somme du coefficient au-dessus de lui et du coefficient en haut à gauche (voir illustration).
Le zoom est accessible dans la version Premium.
Questions préliminaires :
1. Que valent les coefficients de la première colonne ? De la diagonale ?
1. Que valent les coefficients de la première colonne ? De la diagonale ?
2.
En utilisant la relation de Pascal, construire « à la main » la cinquième
ligne du triangle de Pascal.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Construire le triangle de Pascal de proche en
proche en utilisant une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
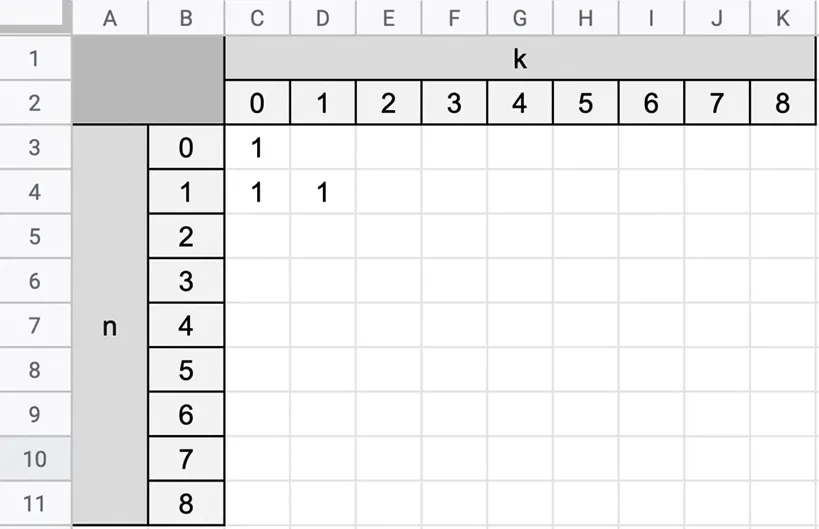
Méthode 1Tableur
1.
Recopier le tableau ci-dessous et compléter la colonne C. (Fichier téléchargeable .)
Le zoom est accessible dans la version Premium.
2.
Quelle formule doit-on saisir puis glisser vers le bas dans la cellule D5 ?
3. Compléter le tableau en saisissant les formules manquantes.
4. Dans la colonne L, afficher pour chaque ligne du tableau la somme des coefficients sur cette ligne.
Quel résultat du cours retrouve‑t‑on ?
3. Compléter le tableau en saisissant les formules manquantes.
4. Dans la colonne L, afficher pour chaque ligne du tableau la somme des coefficients sur cette ligne.
Quel résultat du cours retrouve‑t‑on ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
On souhaite écrire une fonction en Python qui renvoie, pour un entier naturel n donné, les n premières lignes du triangle de Pascal.
La ligne 2 sert à construire un tableau de n lignes et n colonnes rempli de 0.
La ligne 2 sert à construire un tableau de n lignes et n colonnes rempli de 0.
def pascal(n) :
l = [ [0]*n for x in range(n)]
for i in range(n) :
for j in range(n) :
if j == 0 :
l[i][j] = ...
elif ... :
l[i][j] = ...
else :
l[i][j] = ...
return(l)
1.
Compléter la ligne 6 du programme.
2. Un autre cas doit être traité aux lignes 7 et 8. Lequel et de quelle manière ?
3. En utilisant la relation de Pascal, compléter la ligne 10.
4. Pour n fixé, vérifier que l'on retrouve bien l'identité suivante : \displaystyle\sum_{k=0}^{n}\left(\begin{array}{l} n \\ k \end{array}\right)=2^{n}.
2. Un autre cas doit être traité aux lignes 7 et 8. Lequel et de quelle manière ?
3. En utilisant la relation de Pascal, compléter la ligne 10.
4. Pour n fixé, vérifier que l'on retrouve bien l'identité suivante : \displaystyle\sum_{k=0}^{n}\left(\begin{array}{l} n \\ k \end{array}\right)=2^{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Soient a et b deux réels et n un entier naturel. La formule du binôme de Newton stipule que
(a+b)^{n}=\displaystyle\sum_{k=0}^{n}\left(\begin{array}{l}n \\ k\end{array}\right) a^{k}\ b^{n-k}.
Démontrer cette formule en utilisant un raisonnement par récurrence.
Démontrer cette formule en utilisant un raisonnement par récurrence.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah