Activités

Un club de vacances propose trois activités durant la semaine : randonnée, canoë et découverte culinaire. Parmi les 180 vacanciers, 70 se sont inscrits à la randonnée, 80 au canoë et 60 à la découverte culinaire.

Chaque vacancier peut choisir de faire de 0 à 3 activités durant ses vacances.
Combien de programmes différents un vacancier peut‑il construire ?

Pourquoi peut-on affirmer que certains vacanciers se sont inscrits à plusieurs activités ?

Pour résumer la situation, les organisateurs décident de consigner les informations dans le diagramme ci‑contre appelé diagramme de Venn. On peut y lire que 17 personnes sont inscrites à la découverte culinaire et au canoë mais pas à la randonnée.

a) Compléter ce diagramme en sachant que 25 personnes sont inscrites au canoë et à la randonnée mais pas à la découverte culinaire et que personne n’est inscrit à la fois à la randonnée et à la découverte culinaire.

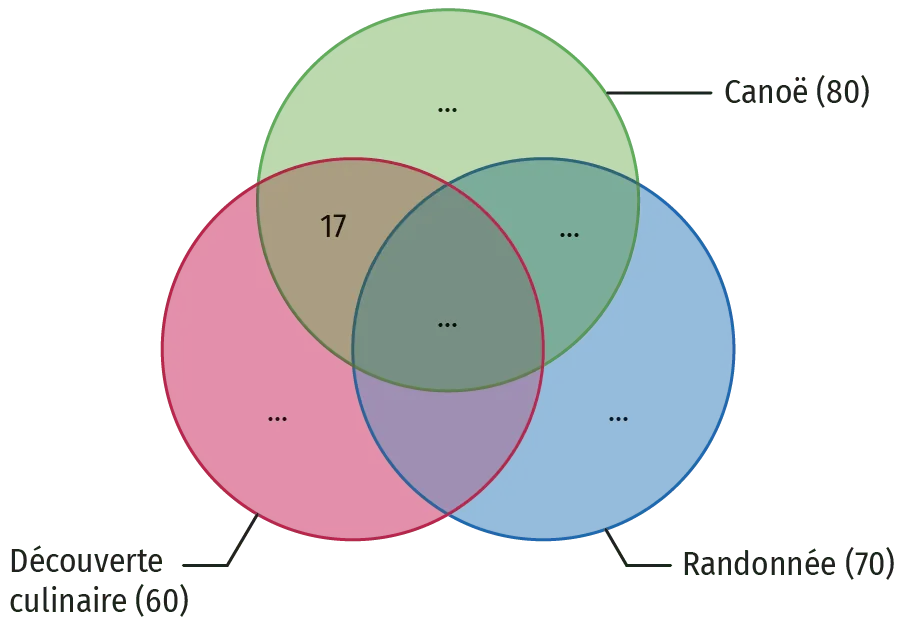
Pour écrire sur ce schéma, veuillez cliquer sur l'image et utiliser notre outil de dessin.


b) Combien de personnes ne sont inscrites à aucune activité ?

On appelle cardinal d’un ensemble le nombre d’éléments de cet ensemble. On note $\text{D}$, $\text{C}$ et$\text{ R}$ l’ensemble des vacanciers inscrits respectivement à la découverte culinaire, au canoë et à la randonnée.

À l’aide du diagramme complété, donner les cardinaux des ensembles $\text{R, C, D}$, $\mathrm{R} \cup \mathrm{D}$ et $\mathrm{C} \cup \mathrm{D}$.

On note $\operatorname{Card}(\mathrm{R})$ le cardinal de l’ensemble $\text{R}$. Quelle relation obtient‑on entre $\operatorname{Card}(\mathrm{R})$, $\operatorname{Card}(\mathrm{D})$ et $\operatorname{Card}(\mathrm{R} \cup \mathrm{D})$ ?

A‑t‑on une relation similaire entre $\operatorname{Card}(\mathrm{C})$, $\operatorname{Card}(\mathrm{D})$ et $\operatorname{Card}(\mathrm{C} \cup \mathrm{D})$ ? Justifier.


À la fin de la semaine de vacances, des prix sont décernés pour chacune de ces activités. Pour chacune d’elle, l’organisation du club désigne le meilleur vacancier ou la meilleure vacancière et lui offre une récompense. On forme ainsi un triplet de vacanciers récompensés.
Combien de triplets de récompensés peut‑on former ? (On suppose qu’un vacancier peut être récompensé pour plusieurs disciplines différentes.)
On appelle produit cartésien des ensembles $\text{C}$, $\text{D}$ et $\text{R}$ l’ensemble des triplets formés à partir d’un élément de chacun de ces ensembles.

Une urne contient quatre boules (une rouge, une jaune, une verte, une bleue) indiscernables au toucher. On tire, successivement et au hasard, trois boules de cette urne et l’on note à chaque fois la couleur de la boule tirée. Par exemple, si on tire successivement une boule rouge, une boule jaune puis une boule verte, on notera ce tirage $(\mathrm{R}\,; \mathrm{J}\,;\mathrm{V})$.

Tirages avec ordre et remise. Dans cette première expérience, la boule tirée est remise avec les autres dans l’urne.
a) Combien a‑t‑on d’issues possibles ?


b) Dénombrer tous les résultats pour lesquels la première boule tirée n’est pas verte.


c) Dénombrer tous les résultats pour lesquels la première boule tirée est verte.


Tirages avec ordre et remise. Dans cette seconde expérience, la boule tirée n’est pas remise dans l’urne.
a) Citer trois issues de l’expérience précédente qui sont désormais impossibles à obtenir.


b) Combien a‑t‑on d’issues possibles ?


c) Dénombrer tous les résultats pour lesquels la première boule tirée n’est pas bleue.

On possède un jeu de dix cartes, numérotées de 1 à 10. De ce paquet, on tire trois cartes et on regarde les nombres obtenus. Les cartes tirées ne sont pas remises dans le paquet.

Tirage avec ordre :
On tire les trois cartes et on les dévoile une par une. Si on tire la carte 1, puis la carte 5, puis la carte 3, on écrira ce tirage (1 ; 5 ; 3).

a) Combien a‑t‑on de possibilités pour la première carte ?


b) Une fois la première carte dévoilée, combien de possibilités reste‑t‑il pour la deuxième carte ?


c) Finalement, avec cette méthode, combien existe‑t‑il de tirages différents ?


Tirage sans ordre :
Ici, les trois cartes du paquet ne sont dévoilées qu’à la fin, l’ordre des cartes n’important pas.

a) Combien de tirages avec ordre mènent au tirage sans ordre {1 ; 5 ; 3} ?




b) Combien existe-t-il de tirages de trois cartes sans tenir compte de l’ordre (combinaison de trois cartes parmi dix) ?


c) Établir une relation entre le nombre de tirages tenant compte de l’ordre de trois cartes parmi dix et le nombre de tirages ne tenant pas compte de l’ordre de trois cartes parmi dix.