Arrangements et permutations

Parcours 1 : exercices

51

;

60

;

70

;

76

;

83

;

95

et

99

Parcours 2 : exercices

55

;

71

;

86

et

102

Parcours 3 : exercices

63

;

82

;

87

et

98

74

Effectuer les calculs suivants sans utiliser la calculatrice.

1. Montrer que, pour tout entier naturel n, on a :

(n+1) ! \geqslant n !

2. Dans quel cas a-t-on égalité ?

75

[ Raisonner. ]
On souhaite construire de nouveaux mots avec les lettres du mot MATHS. On ne se souciera pas de savoir si les mots obtenus ont un sens ou non. Chaque lettre ne peut être utilisée qu'une seule fois.

1. Combien de mots de trois lettres peut‑on construire :
a. sans restriction ?

b. sachant que le A est en première position ?

c. sans utiliser la lettre T ?

2. Combien de mots de cinq lettres peut‑on construire :
a. sans restriction ?

b. sachant que le T est en troisième position et le S en dernière position ?

76

[ Calculer. ]
Soit n un entier naturel. Simplifier les nombres suivants.

1. (n+1) \times n !

2. \frac{(n-5) !}{(n-7) !}, (n \geqslant 7)

3. \frac{(n+2) !}{(n+1)(n+2)}

4. \frac{1}{(n+1) !}-\frac{1}{n !}

77

[ Calculer. ]
Soit n un entier naturel. Simplifier les nombres suivants.
1. \frac{n ! \times(n+2) !}{(n !)^{2}}

2. \frac{(n+1) !}{n !}-\frac{n !}{(n-1) !}, (n \geqslant 1)

3. \frac{(2(n+1)) !}{(2 n+1) !}

4. \frac{1}{(n-2) !}-\frac{1}{n !}, (n \geqslant 2)

78

[ Modéliser. ]
1. Sur tableur, entrer dans la colonne A les entiers de 1 à 30. Dans la colonne B, calculer la factorielle (fonction FACT sur tableur) de ces nombres. 2. Soit n un entier naturel non nul. On note \text{S}(n) le nombre \sqrt{2 \pi n}\left(\frac{n}{\mathrm{e}}\right)^{n}. Dans la colonne C du tableur, entrer les images par \text{S} des nombres de la colonne A. 3. Comparer ces nombres avec ceux de la colonne B.

79

[ Modéliser. ]
Écrire une fonction factorielle en Python qui prend en entrée un entier naturel n et qui renvoie n!.

80

[ Chercher. ]
Soient \text{A} et \text{B} deux ensembles finis, non vides et disjoints, de cardinaux respectifs n et p.
1. Combien de permutations de \text{A}\cup\text{B} existe-t-il ?

2. Combien de permutations de \text{A}\cup\text{B} existe‑t‑il si on veut que les éléments de \text{A} et de \text{B} ne soient pas mélangés ?

81

[ Raisonner. ]
Résoudre l'équation suivante d'inconnue n \in \mathbb{N}:

(n+2) !=6 n !

82

[ Raisonner. ]
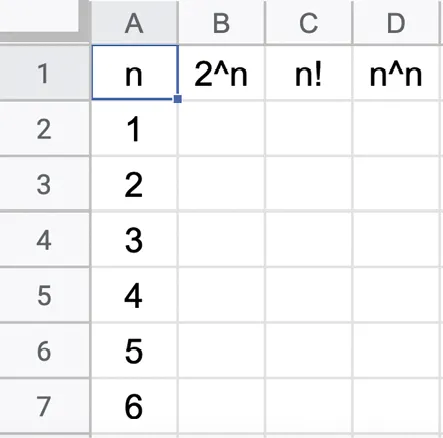
On souhaite déterminer les valeurs de n \in \mathbb{N}^{*} pour lesquelles 2^{n} \leqslant n ! \leqslant n^{n}. 1. Quelles formules doivent être entrées dans les cellules B2 et D2 puis glissées vers le bas dans ce tableau ?

2. Quel nombre doit-on entrer dans la cellule C2 ?

3. Quelle formule doit-on entrer dans la cellule C3 puis glisser vers le bas pour calculer les factorielles des entiers considérés ici sans utiliser la fonction FACT du tableur ?

4. À partir de quel entier n semble-t-on avoir 2^{n} \leqslant n ! \leqslant n^{n} ?

5. Démontrer cette conjecture.

83

[ Chercher. ]
Combien d'entiers naturels distincts pourrait‑on constituer avec trois chiffres différents choisis entre 0 et 9 inclus, chaque chiffre ne pouvant être utilisé qu'une seule fois ?

84

[ Chercher. ]
Pour réviser ses devoirs à venir, Mathilde décide d'organiser on week-end : ce samedi, elle fera une heure de mathématiques, une heure de physique‑chimie, une heure de philosophie et une heure de LVA.

1. Combien d'emplois du temps différents Mathilde peut-elle avoir ?

2. Mathilde décide de regrouper les mathématiques et la physique-chimie en un seul bloc. Combien a-t-elle alors d'emplois du temps possibles ?

85

[ Raisonner. ]
Un professeur a préparé un exercice à faire sur une application. Il a utilisé dix questions.
L'application en choisit cinq au hasard et les propose les unes après les autres.
Combien de suites différentes d'exercices peut-on obtenir ?

86

[ Chercher. ]
Pour créer le logo d'un club de mathématiques, on propose d'écrire le mot MATHS et d'en colorer les lettres.
On dispose de cinq couleurs différentes.

1. Combien de coloriages différents est‑il possible de réaliser si l'on peut utiliser une même couleur plusieurs fois ?

2. Même question si l'on ne souhaite utiliser chaque couleur qu'une seule fois.

3. Même question si l'on souhaite que deux lettres adjacentes ne soient pas de la même couleur.

4. On souhaite également ajouter un fond coloré derrière le logo. La couleur de ce fond ne peut alors pas être utilisée pour les lettres. Reprendre les questions 1 à 3 en prenant en compte cette nouvelle information.

87

[Raisonner.]
On dispose des chiffres 0, 1, 2 et 3.

1. Combien de nombres à quatre chiffres distincts peut‑on construire à partir de ces quatre chiffres :
a. en autorisant le 0 en première position ?

b. en interdisant le 0 en première position ?

2. Combien de nombres à trois chiffres distincts peut-on constituer à partir de ces quatre chiffres :
a. en interdisant le chiffre 0 en première position ?

b. en autorisant le chiffre 0 en première position et en obligeant le nombre obtenu à être multiple de 3.