Mathématiques Terminale Spécialité
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 6
TP INFO 2
Méthode de la sécante
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soit f la fonction définie sur \mathbb{R} par f(x)=(x+1) \mathrm{e}^{x}+x.
On appelle \mathcal{C}_f la courbe représentative de f dans un repère (\mathrm{O}\,; \overrightarrow{i}\,, \overrightarrow{j}).
On désire obtenir un encadrement de la solution de l'équation f(x) = 0 par la méthode de la sécante.
Pour cela, on localise une solution \alpha de l'équation f(x) = 0 sur [-1\,;0], on utilise la corde reliant les points de coordonnées respectives (-1\,;f(-1)) et (0\,;f(0)) et l'intersection de cette corde avec l'axe des abscisses pour remplacer [-1\,;0] par un autre intervalle plus petit contenant \alpha. On posera \mathrm{M}_{i} le point de coordonnées \left(x_{i}\,;f\left(x_{i}\right)\right).
Questions préliminaires :
1. Étudier les variations de f sur \mathbb{R}.
2. En déduire que l'équation f(x) = 0 admet une unique solution \alpha \in[-1\,;0].
3. Soient \mathrm{M}_{0} et \mathrm{M}_{1} les deux points de \mathcal{C}_f d'abscisses respectives -1 et 0. Montrer que la droite \left(\mathrm{M}_{0} \mathrm{M}_{1}\right) coupe l'axe des abscisses au point d'abscisse -0{,}5.
On désire obtenir un encadrement de la solution de l'équation f(x) = 0 par la méthode de la sécante.
Pour cela, on localise une solution \alpha de l'équation f(x) = 0 sur [-1\,;0], on utilise la corde reliant les points de coordonnées respectives (-1\,;f(-1)) et (0\,;f(0)) et l'intersection de cette corde avec l'axe des abscisses pour remplacer [-1\,;0] par un autre intervalle plus petit contenant \alpha. On posera \mathrm{M}_{i} le point de coordonnées \left(x_{i}\,;f\left(x_{i}\right)\right).
Questions préliminaires :
1. Étudier les variations de f sur \mathbb{R}.
2. En déduire que l'équation f(x) = 0 admet une unique solution \alpha \in[-1\,;0].
3. Soient \mathrm{M}_{0} et \mathrm{M}_{1} les deux points de \mathcal{C}_f d'abscisses respectives -1 et 0. Montrer que la droite \left(\mathrm{M}_{0} \mathrm{M}_{1}\right) coupe l'axe des abscisses au point d'abscisse -0{,}5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Obtenir un encadrement de \alpha par la méthode de la sécante en utilisant une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
1. À l'aide de GeoGebra, tracer \mathcal{C}_f et les axes comme indiqué ci‑dessous.
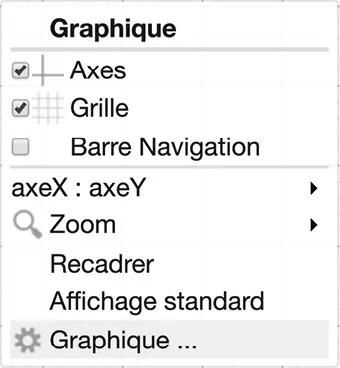
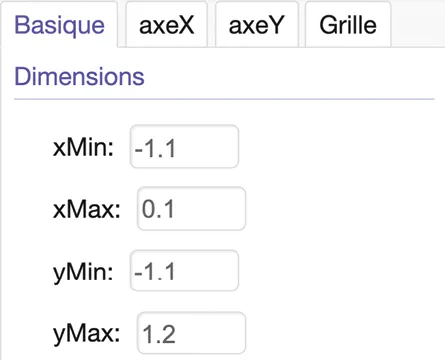
2. a. Sur \mathcal{C}_f, placer les points \mathrm{M}_0 d'abscisse -1 et \mathrm{M}_1 d'abscisse 0.
b. Placer le point d'intersection \mathrm{C}_1 de \left(\mathrm{M}_{0} \mathrm{M}_{1}\right) et de l'axe des abscisses.
3. \mathrm{M}_2 est le point de \mathcal{C}_f de même abscisse que \mathrm{C}_1. Construire le point \mathrm{C}_2 suivant le même procédé.
4. Déterminer une valeur arrondie à 10^{-2} près de l'abscisse de \mathrm{C}_2.
2. a. Sur \mathcal{C}_f, placer les points \mathrm{M}_0 d'abscisse -1 et \mathrm{M}_1 d'abscisse 0.
b. Placer le point d'intersection \mathrm{C}_1 de \left(\mathrm{M}_{0} \mathrm{M}_{1}\right) et de l'axe des abscisses.
3. \mathrm{M}_2 est le point de \mathcal{C}_f de même abscisse que \mathrm{C}_1. Construire le point \mathrm{C}_2 suivant le même procédé.
4. Déterminer une valeur arrondie à 10^{-2} près de l'abscisse de \mathrm{C}_2.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
On construit la suite (x_i) de la manière suivante :
x_i est l'abscisse du point d'intersection de la sécante \left(\mathrm{M}_{i-2} \mathrm{M}_{i-1}\right) avec l'axe des abscisses pour i \geqslant 2.
On pose x_0 = -1 et x_1 = 0 (abscisses respectives de \mathrm{M}_{0} et \mathrm{M}_{1}). On obtient alors la formule de récurrence suivante :
On définit enfin le taux d'accroissement par :
x_i est l'abscisse du point d'intersection de la sécante \left(\mathrm{M}_{i-2} \mathrm{M}_{i-1}\right) avec l'axe des abscisses pour i \geqslant 2.
On pose x_0 = -1 et x_1 = 0 (abscisses respectives de \mathrm{M}_{0} et \mathrm{M}_{1}). On obtient alors la formule de récurrence suivante :
x_{n+1}=x_{n}-\frac{x_{n}-x_{n-1}}{f\left(x_{n}\right)-f\left(x_{n-1}\right)} f\left(x_{n}\right).
On définit enfin le taux d'accroissement par :
\frac{f\left(x_{n}\right)-f\left(x_{n-1}\right)}{x_{n}-x_{n-1}}.
1. Écrire une fonction f sur Python qui retourne l'image f(x) de x par la fonction f.
2. Compléter la fonction secante ci‑dessous retournant un encadrement de \alpha.
3. Obtenir un encadrement de \alpha à 10^{-3} près.
from math import * def f(x): return... def secante(a, b, epsilon): x1, x2 = a, b accroissement = (f(x2) - f(x1))/(x2 - x1) while abs(x2 - x1) > epsilon: x1 = x2 x2 = ... accroissement = ... return x1, x2
3. Obtenir un encadrement de \alpha à 10^{-3} près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
