Mathématiques Terminale Spécialité
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 7
TP INFO 2
Approximation d'une fonction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soit f une fonction définie et dérivable n fois sur un intervalle \mathrm{I}. Soit a \in \mathrm{I}. Alors, pour tout x \in \mathrm{I}, on a
f(x)=f(a)+(x-a) f^{\prime}(a)+\frac{(x-a)^{2}}{2 !} f^{\prime \prime}(a)+\ldots+\frac{(x-a)^{n}}{n !} f^{(n)}(a)+(x-a)^{n} \mathrm{R}(x)
où \text{R} est une fonction définie au voisinage de a telle que \lim \limits_{\substack{x \rightarrow a}} \mathrm{R}(x)=0.
C'est ce qu'on appelle le développement limité de f en a à l'ordre n.
On rappelle que, pour tout entier n \geqslant 1, n !=1 \times 2 \times \ldots \times n.
où \text{R} est une fonction définie au voisinage de a telle que \lim \limits_{\substack{x \rightarrow a}} \mathrm{R}(x)=0.
C'est ce qu'on appelle le développement limité de f en a à l'ordre n.
On rappelle que, pour tout entier n \geqslant 1, n !=1 \times 2 \times \ldots \times n.
Questions préliminaires :
1. Écrire le développement limité de f à l'ordre 1 en a. De quelle approximation s'agit‑il ?
2. On suppose que 0 \in \mathrm{I}. Que devient le développement limité à l'ordre n de la fonction f en a = 0 ?
On admet que (x-a)^{n} \mathrm{R}(x) est négligeable et que l'on peut donc écrire l'approximation polynomiale à l'ordre n suivante : f(x) \approx f(a)+(x-a) f^{\prime}(a)+\frac{(x-a)^{2}}{2 !} f^{\prime \prime}(a)+\ldots+\frac{(x-a)^{n}}{n !} f^{(n)}(a).
1. Écrire le développement limité de f à l'ordre 1 en a. De quelle approximation s'agit‑il ?
2. On suppose que 0 \in \mathrm{I}. Que devient le développement limité à l'ordre n de la fonction f en a = 0 ?
On admet que (x-a)^{n} \mathrm{R}(x) est négligeable et que l'on peut donc écrire l'approximation polynomiale à l'ordre n suivante : f(x) \approx f(a)+(x-a) f^{\prime}(a)+\frac{(x-a)^{2}}{2 !} f^{\prime \prime}(a)+\ldots+\frac{(x-a)^{n}}{n !} f^{(n)}(a).
3. Soit f la fonction définie sur [-1 ;+\infty[ par f(x)=\sqrt{1+x}. On se place uniquement sur l'intervalle \mathrm{I}=]-1 ;+\infty[ sur lequel la fonction f est deux fois dérivable.
Démontrer que l'approximation polynomiale à l'ordre 2 de f en 0 est f(x) \approx 1+\frac{1}{2} x-\frac{1}{8} x^{2}.
Démontrer que l'approximation polynomiale à l'ordre 2 de f en 0 est f(x) \approx 1+\frac{1}{2} x-\frac{1}{8} x^{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
À l'aide d'une des deux méthodes, utiliser les développements limités pour obtenir une approximation de plus en plus précise de la fonction f, définie ci‑dessus, en 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
Ouvrir une nouvelle fenêtre graphique GeoGebra.
GeoGebra
1. Dans la ligne de saisie, définir la fonction f.
2. Créer un curseur n allant de 0 à 10 avec un pas de 1.
3. On souhaite créer la fonction g correspondant à l'approximation polynomiale de f en 0 donnée par son développement limité à l'ordre n.
Pour cela, créer la fonction g de la façon suivante.
4. En fonction des différentes valeurs de n, décrire la courbe représentative de g en fonction de celle de f sur l'intervalle [-0{,}5\,; 0{,}5].
5. Afin de mieux se rendre compte de l'approximation, créer la fonction h définie, pour tout x \in \mathrm{I}, par h(x)=f(x)-g(x) et commenter la courbe obtenue.
2. Créer un curseur n allant de 0 à 10 avec un pas de 1.
3. On souhaite créer la fonction g correspondant à l'approximation polynomiale de f en 0 donnée par son développement limité à l'ordre n.
Pour cela, créer la fonction g de la façon suivante.
4. En fonction des différentes valeurs de n, décrire la courbe représentative de g en fonction de celle de f sur l'intervalle [-0{,}5\,; 0{,}5].
5. Afin de mieux se rendre compte de l'approximation, créer la fonction h définie, pour tout x \in \mathrm{I}, par h(x)=f(x)-g(x) et commenter la courbe obtenue.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
On note g l'approximation polynomiale de f en 0 donnée par son développement limité d'ordre n.
1. Reproduire la feuille de calcul ci‑dessous pour x variant de -0{,}9 à 1 avec un pas de 0{,}1. (Fichier téléchargeable .)
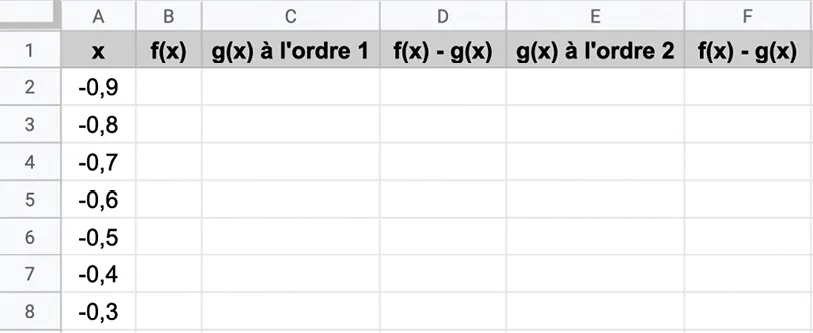
2. a. Compléter la colonne B pour obtenir les images de x par f.
b. Quelles formules faut‑il écrire dans les cellules C2 et D2 ? Compléter alors les colonnes C et D.
2. a. Compléter la colonne B pour obtenir les images de x par f.
b. Quelles formules faut‑il écrire dans les cellules C2 et D2 ? Compléter alors les colonnes C et D.
3. a. Compléter les colonnes E et F pour obtenir les images de x par une approximation de f à l'ordre 2.
b. Cette approximation est‑elle meilleure que celle à l'ordre 1 ? Justifier.
4. Une approximation de f à l'ordre 3 est f(x) \approx 1+\frac{1}{2} x-\frac{1}{8} x^{2}+\frac{1}{16}x^{3}.
Une approximation de f à l'ordre 4 est f(x) \approx 1+\frac{1}{2} x-\frac{1}{8} x^{2}+\frac{1}{16}x^{3}-\frac{5}{64} x^{4}.
Compléter les colonnes G, H, I et J sur le même modèle que précédemment, puis comparer les différentes approximations.
b. Cette approximation est‑elle meilleure que celle à l'ordre 1 ? Justifier.
4. Une approximation de f à l'ordre 3 est f(x) \approx 1+\frac{1}{2} x-\frac{1}{8} x^{2}+\frac{1}{16}x^{3}.
Une approximation de f à l'ordre 4 est f(x) \approx 1+\frac{1}{2} x-\frac{1}{8} x^{2}+\frac{1}{16}x^{3}-\frac{5}{64} x^{4}.
Compléter les colonnes G, H, I et J sur le même modèle que précédemment, puis comparer les différentes approximations.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
